Розділ 4. ОЦІНКА НАДІЙНОСТІ СТИСНУТО-ЗІГНУТИХ ЕЛЕМЕНТІВ
Особливості імовірнісного розрахунку стиснуто-зігнутих елементів
4.1.1. Особливості роботи стиснуто-зігнутих елементів. На стиск зі згином працюють елементи, завантажені, крім поздовжньої сили, поперечним навантаженням або згинальним моментом (рис. 4.1, а). Такими елементами є колони виробничих будівель постійного перерізу і ступінчасті, стійки фахверка, стержні кроквяних ферм з позавузловим навантаженням. Ці елементи (рис. 4.1, а) є по суті самими малодослідженими з точки зору надійності будівельних конструкцій.
Таке положення обумовлене тим, що окрім труднощів з імовірнісним описом реальних навантажень, завдання оцінки надійності стиснуто-зігнутих елементів каркасів виробничих будівель, у тому числі і виконаних з такого добре вивченого і чітко працюючого матеріалу, яким є сталь, пов'язана з урахуванням геометричної і фізичної нелінійності. Між тим імовірнісний аналіз таких елементів, особливо в частині обґрунтованого розрахунку сполучення зусиль, може дати помітний ефект, оскільки на практиці саме стиснуто-зігнуті елементи (стійки, колони та ін.) завантажені найбільш широким набором випадкових навантажень.
Проілюструємо на рис. 4.1,б (крива О-С) роботу (поведінку) сталевого стиснуто-зігнутого стержня. Тут по осі абсцис відкладений прогин стержня, по осі ординат – нормальне напруження 
(
– поздовжня сила, А – площа перерізу стержня). З самого початку завантаження стержень викривляється, у міру зростання навантажень прогин стержня і згинаючий момент в ньому ростуть.
Точка А на графіці відповідає досягненню крайової текучості, коли в найбільш напружених фібрах найбільш небезпечного перерізу стержня нормальне напруження дорівнює межі текучості. Цей момент і напруження 
, що відповідає йому, є граничними для пружного розрахунку за деформованою схемою.
Далі діаграма роботи пружного стержня відхиляється вгору (ділянка А - G) і у міру необмеженого зростання прогину асимптотично наближається до рівня Ейлерового критичного напруження для центрово-стиснутого стержня:
, (4.1)
де Е – модуль пружності сталі; I – момент інерції стержня; l – геометрична довжина стержня; 
– коефіцієнт розрахункової довжини,що враховує вид закріплення кінців стержня; А – площа перерізу; 
– гнучкість стержня; 
– радіус інерції перерізу.
Рис. 4.1. До розрахунку стиснуто-зігнутих елементів
а – схема елемента; б – стадії роботи стиснуто-зігнутих
і центрово-стиснутих елементів; в – похибка пружного розрахунку
Роботу реального сталевого стержня відображає ділянка кривої А-С, що має максимум в точці В, який відповідає критичному стану стержня і критичному напруженню 
. Для реальних сталевих стиснуто-зігнутих стержнів рівність 
відповідає граничному стану і припиненню експлуатації, а умова неруйнівності матиме наступний вигляд:
(4.1)
На графіці рис. 4.1, б ілюструються також стадії роботи центрально-стисненого стержня: стійка прямолінійна (при відсутності початкової недосконалості) – ділянка O-D осі ординат до 
; ділянка Д-E роздвоєння форм рівноваги, що відповідає критичному стану, і низхідна ділянка Е- F нестійкого посткритичного стану.
Пружний розрахунок з урахуванням геометричної нелінійності може бути застосовний для стиснуто-зігнутих стержнів великої гнучкості, для яких точки А і В на графіці рис. 4.1,б зближуються, для стержнів із сталей підвищеної міцності без вираженого майданчика текучості, а також в методах, що враховують пружно-пластичну роботу сталі введенням відповідних поправок [00]. На рис. 4.1, в ілюструється похибка пружного розрахунку в залежності від гнучкості 
і відносного ексцентриситету поздовжньої сили
, (4.2)
де М – згинальний моменту стержні від поперечного навантаження, W – момент опору перерізу, 
– радіус ядра перерізу.
Графік рис. 4.1,в наочно демонструє помітну наближеність пружного розрахунку стиснуто-зігнутих елементів. Тому розрахунок таких елементів згідно з нормами проектування [00] проводиться з урахуванням розвитку пластичності; аналогічний підхід застосовується для оцінки їхньої надійності.
4.1.2. Імовірнісний аналіз стиснуто-зігнутих елементів. Визначимо стохастичну природу умови неруйнівності (4.1), обидва члени якої є квазістаціонарними функціям часу в просторі нормальних напружень. Внаслідок цього відмова моделюється як перетин квазістаціонарною траєкторією 
квазістаціонарної межі області допустимих станів (рис. 4.2, а).
Рис. 4.2. Особливості імовірнісного розрахунку стиснуто-зігнутих елементів:
а, б – моделі відмов; в – лінеаризація функції одного аргументу
Представляється зручнішим змінити параметр якості системи і вид допустимої області. Для цього перетворимо нерівність (4.1):
; 
(4.3)
де 
– функція, що приводить критичне напруження втрати стійкості стиснуто-зігнутого стержня до межі плинності матеріалу; приміром, в чинних нормах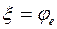 
[00].
Тоді для резерву несучої здатності, який для цього стержня назвемо резервом стійкості, маємо:
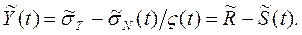(4.4)
Межа допустимої області Г при цьому залишається випадковою, незалежною від часу (оскільки ми не враховуємо зміну міцності елементів), а відмова трактується як вихід квазістаціонарної траєкторії 
за випадковий рівень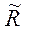 
(рис. 4.2, б).
4.1.3. Лінеаризація функцій. У зв'язку із складністю послідовного стохастичного аналізу поведінки стиснуто-зігнутих стержнів будемо використовувати прийом з підставлянням імовірнісних параметрів в детерміністичні рішення завдань стійкості таких стержнів.
У загальному випадку резерв стійкості стиснуто-зігнутих стержнів є функцією кількох аргументів:
. (4.5)
Внаслідок нелінійності функції виконаємо її лінеаризацію із заміною вихідного виразу (4.5) лінійною функцією виду [51]:
(4.6)
На рис. 4.2, в ілюструється лінеаризація функції одного аргументу, вона виконується в околі математичного сподівання функції, цьому кутовий коефіцієнт прямої, що вводиться, визначається частковим диференціюванням вихідної функції по відповідному аргументу. Геометричним зображенням лінеаризованої функції n aргументів є гіпер-пряма в n+1 мірному просторі. Похибку у визначенні 
у зв'язку з лінеаризацією по (4.6) можна оцінити наступним виразом:
Тут 
– дисперсія i - го аргументу.
При незначності цієї похибки формула для визначення математичного сподівання (4.6) спрощується і зводиться до підстановки математичних сподівань аргументів у вихідну функцію:
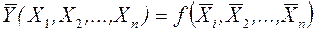. (4.8)
Середньоквадратичне відхилення (стандарт) резерву стійкості визначається, у випадку незалежності аргументів, як
(4.9)
Похибка даного виразу внаслідок лінеаризації оцінюється так [51]:
(4.10)
Якщо аргументи кореляційно зв’язані між собою, формула (4.9) стає наступною [51]:
, (4.11)
де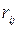 
- коефіцієнт кореляції аргументів 
і 
.
На базі цього підходу і числового прикладу (приведеного нижче в п. 4.2.2) був проведений аналіз застосовності операції лінеаризації до задачі, що розглядається. Ординати лінійної функції (4.6) були зіставлені з точними значеннями вихідної функції Y, обчисленої за формулою (4.5) з використанням (4.12). Розбіжність була отримана незначною для досить широкого інтервалу зміни функції Y: при відхиленні усіх аргументів на величину одного стандарту 
, що призводить до відхилення Y приблизно на 
, лінеаризоване значення функції відхиляється від точного всього на - 3,1%. При збільшенні відхилення аргументів до двох стандартів, що призводить до відхилення резерву стійкості від математичного очікування на 
, різниця між точним і наближеним значеннями функції Y складає - 10,3%.
Обчислені за формулами (4.7) і (4.10) похибки математичного очікування і дисперсії виявилися незначними і не перевищили 0,1%.
Враховуючи малу похибку при обчисленні резерву стійкості, його математичного очікування і дисперсії, операцію лінеаризації для завдань імовірнісного розрахунку стиснуто-зігнутих сталевих стержнів можна вважати обґрунтованою, щонайменше, для умов, близьких до умов розглянутого прикладу.
Надійність сталевих стиснуто-зігнутих елементів постійного перерізу
4.2.1. Виведення основних формул. Для суцільностінчастих стержнів, що розглядаються в площині дії моменту, співпадаючої з площиною симетрії, для значень 
по таблиці 74 [294] підібрана функція виду
; 
; 
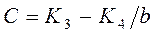, 4.12)
де К1 = 0,70; К2 = 0,62; К3 = 0,943; К4 = 0,075; 
– приведений відносний ексцентриситет; 
– коефіцієнт, що враховує форму перерізу і орієнтацію ексцентриситету (табл. 00 [294]); 
– відносний ексцентриситет (формула (4.2)); 
– умовна гнучкість елементу.
На рис. 4.3, в, де показана залежність 
від 
і 
, видно, що функція (4.12) досить точно враховує характер зміни коефіцієнту 
, апроксимуючи його знизу, тобто "в запас". Проведений на ПЕОМ розрахунок показав, що в інтервалі значень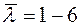 
і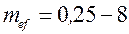 
Рис. 4.3. До розрахунку стиснуто-зігнутих стійок:
а – стійка постійного перерізу; б – ступінчаста колона; в – графіки коефіцієнту 
: за табл. 74 СНиП [294]; 
_._._за формулою (4.11)
відмінність розрахункових величин за формулою (4.12) від нормативних значень не перевищує 
10%
З використанням формули (4.12) вираз для резерву стійкості матиме наступний вигляд
. (4.13)
Математичне сподівання резерву стійкості, згідно з (4.8)
. (4.14)
Частинним диференціюванням визначаємо коефіцієнти для визначення стандарту 
:
; 
; 
. (4.15)
Тут d = 0,4343... – модуль переходу від натуральних логарифмів до десяткових.
Виведені формули дозволяють одержати оцінку надійності стиснуто-зігнутого елемента.
4.2.2. Числовий приклад. Визначити імовірність відмови сталевої стійки постійного перерізу, завантаженої випадковою поздовжньою силою 
і рівномірно розподіленим поперечним навантаженням 
(рис. 4.3, а).
Вихідні дані. Довжина стійки 10 м.Статистичні характеристики поздовжньої сили (у кН):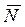 
= 700, 
= 150; поперечного навантаження (у кН/м): 
, 
; межі текучості стали (у МПа):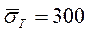 
, 
. Переріз стійки підібрано на детерміновані навантаження N = 1000 кН і q = 10 кН/м і отримано у вигляді прокатного двотавра №50 при 
= 192 МПа < 
= 230 МПа для сталі С235 [294]. Геометричні характеристики перерізу: площа А = 100см2, момент опору Wx = 1598 см3, радіус інерції 
= 19,9 см.
Рішення. Визначимо числові характеристики згинального моменту:
= 68,7кНм;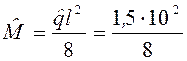 
= 18,8кНм.
По наведеним вище залежностям виконаємо обчислення, використовуючи параметри підібраної сталевої стійки:
; 
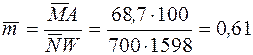=1,531·0,61=0,934; 
50,3; 
; 
; 
.
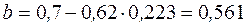Визначимо числові характеристики резерву стійкості стійки.
Математичне сподівання за формулою (4.14):
МПа.
Коефіцієнти за формулами (4.15) дорівнюють:
1/см2;
1/см3.
Стандарт резерву стійкості за формулою (4.9):
МПа
Характеристика безпеки виявилася рівною 
, що при нормальному розподілі резерву стійкості дає імовірність відмови стійки 
(додаток, табл. Д.00).
4.2.3. Розрахунок надійності сталевих колон постійного перерізу. Типовий приклад стійки безкранової будівлі, конструкція якої показана на рис. 4.4, а, розрахункова схема на рис. 4.3, а, розглянутий у попередньому пункті. Схема завантаження включає осьову силу, що викликається постійним навантаженням від ваги покриття і сніговим навантаженням, і поперечне розподілене вітрове навантаження. Окрім варіанту, розглянутого в п. 4.2, був розглянутий ще ряд стійок того ж перерізу, перевірених по СНиП [294] так, щоб виконувалася умова 
, схеми завантаження яких відрізнялися співвідношенням напружень від N і М.
Результати оцінки надійності, одержаної у техніці випадкових величин, наведені на рис. 4.4, в у вигляді графіку характеристики безпеки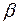 
, який має опуклий характер з максимумом близько СN = 0,5, який приблизно відповідає приведеному вище в п. 4.2 прикладу (точка А на графіці). По мірі збільшення долі моменту або поздовжньої сили графік знижується, плавно без перелому опускаючись до граничних випадків згину і центрального стиску при СN = 0 і СN = 1,0. Різниця крайніх ординат є наслідком різної забезпеченості розрахункових значень моменту(
) і поздовжньої сили (
). Графік рис. 4.4,в цілком очевидно ілюструє можливість введення коефіцієнта сполучення 
для стиснуто-зігнутих елементів.
Імовірнісний розрахунок з урахуванням реально діючих навантажень виконувався для стійок багатопролітного каркаса, оснащеного мостовими кранами, конструкція і розрахункова схема стійки наведена на рис. 4.4, б. Стійки защемлені у фундаменті і шарнірно сполучені з гратчастим ригелем, коефіцієнт розрахункової довжини стійок приймався рівним µ = 0,7. Стійки завантажені випадковими вертикальними силами від постійного і снігового навантажень, горизонтальним і прикладеним з ексцентриситетом вертикальним навантаженням кранів і розподіленим вітровим навантаженням.
Рис. 4.4. Сталеві стиснуто-зігнуті стійки:
а – стійка безкранової будівлі;
б – стійка постійного перерізу будівлі з мостовими кранами;
в – характеристика безпеки стійки.
Таблиця 4.0
