Главная задача изучения рядов динамики состоит в том, чтобы выявить основные тенденции или направленности изменения уровней ряда динамики с целью прогнозирования на будущее экономических показателей деятельности организаций.
Основная тенденция в рядах динамики или тренд определяется тремя методами:
1) метод скользящих средних
2) метод сезонной волны
3) метод аналитического выравнивания
С помощью метода скользящих средних тренд в рядах динамики определяется путем показа плавного изменения изучаемых показателей во времени. Принцип расчета скользящих средних: вычисляется средняя арифметическая простая минимально из трех уровней ряда динамики. Каждая скользящая средняя образуется путем отбрасывания одного уровня слева и присоединения одного уровня справа:
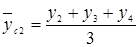
В результате расчета скользящей средней определяются выровненные сглаженные уровни ряда динамики.
Пример: данные о выручке торговой организации за рабочую неделю:
понедельник – 350 т.р.
вторник – 360 т.р.
среда – 280 т.р.
четверг – 270 т.р.
пятница – 350 т.р.
суббота – 600 т.р.
Вычислить скользящую среднюю и построить ряд сглаженных уровней.
т.р.
т.р.
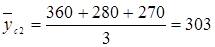т.р.
т.р.
Сглаженные уровни ряда динамики: 330, 303, 300, 407
С помощью скользящей средней были устранены случайные изменения товарооборота в течение рабочей недели и выявлены плавные изменения товарооборота, отражающие основную тенденцию в изучаемом ряду динамики.
Формула расчета сезонной волны:
Где I – индекс, т.е. показатель
_
S = средняя волна
Пример: по данным о товарообороте организации за 3 года вычислить показатели сезонной волны. Распределить товарооборот планируемого года 11200 т.р. по кварталам с учетом сезонной волны.
Таблица № 15
Данные о товарообороте организации
| Квартал | Уровни (уi) товарооборот, т.р. | Сумма уi | _ уi | _ Is | ||
| 1 год | 2 год | 3 год | ||||
| I | 84,7 | |||||
| II | 90,5 | |||||
| III | 107,5 | |||||
| IV | 117,3 | |||||
| ИТОГО: | 2528,75 |
Метод аналитического выравнивания основан на предположении, что основным фактором, влияющим на изменение уровней рядов динамики, является фактор времени, поэтому выявление тренда в рядах динамики с помощью аналитического выравнивания происходит в основном по формуле прямолинейной регрессии:
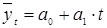
где:
_
уt – теоретическое сглаженные уровни ряда динамики
а0 и а1 – параметры уравнения
t – показатели времени
Для решения уравнения прямолинейной регрессии применяется система нормальных уравнений:
na0 + a1*сумму t = сумма у
а0 * сумму t + a1 * сумму t = сумма ty
Расчет параметров уравнения а0 и а1 можно упростить. Если отсчет времени производить таким образом, чтобы общая сумма показателей времени ряда динамики ровнялась 0. При нечетном количестве уровней ряда динамики показатель времени, находящийся в середине ряда условно принимается за 0. Показатели времени, находящиеся до нулевого значения, обозначаются: -1, -2, -3 и т.д.
Показатели времени, находящиеся после 0 значения обозначаются: +1, +2, +3 и т.д. При четном числе уровней ряда динамики показатели времени, находящиеся до середины ряда, нумеруются: -1, -3, -5 и т.д.
Показатели времени, находящиеся после середины ряда, нумеруются: +1, +3, + 5 и т.д. При этих условиях сумма t = 0 и система нормальных условий уравнений преобразуется:
y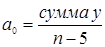 
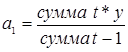
пример: по данным о товарообороте универмага за 5 лет провести аналитическое выравнивание ряда динамики по уравнению прямолинейной регрессии.
Таблица № 16
Товарооборот универмага за 5 лет
| год | т/о, млн.р. (у) | Показатели времени (t) | t | tу | _ уt |
| 4,7 | -2 | -9,4 | 4,76 | ||
| 5,2 | -1 | -5,2 | 5,21 | ||
| 5,8 | 5,66 | ||||
| 6,1 | +1 | 6,1 | 6,11 | ||
| 6,5 | +2 | 6,56 | |||
| ИТОГО: | 28,3 | 4,5 | 28,3 |
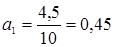
= 5.66 + 0,45*(-2) = 4,76
Теоретическое сглаживание уровней ряда динамики незначительно отличаются от фактических уровней, это объясняется тем, что аналитическое выравнивание ряда динамики позволяет выявить только воздействие постоянного фактора – фактора t.
Экстраполяция
Изучение динамики экономических показателей, выявление тренда в рядах динамики дает основание для определения будущих размеров уровня экономических показателей, т.е. для прогнозирования деятельности организации. Прогнозирование предполагает, что тренд ряда динамики, действовавший в прошлом (внутри ряда динамики) сохраняется и в планируемом будущем, т.е. прогноз основан на экстраполяции.
Экстраполяция – распространение тенденции изменений уровня ряда динамики на будущее.
Возможность экстраполяции объясняется тем, что социально-экономические явления инерционны, т.е. в течение длительного времени сохраняют достигнутый уровень развития.
Методы экстраполяции в рядах динамики:
1) по среднему абсолютному приросту:
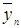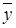+ t = 
+(
)*t
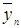+ t – уровни экстраполированного ряда динамики
– последний уровень изучаемого ряда динамики
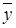– средний абсолютный прирост
t – срок прогноза
2) по среднему темпу роста
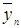+ t = *(
)
3) по уравнению прямолинейной функции
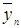+ t = 
+ 
t
пример: данные об издержках обращения торговой организации за 5 лет:
1 год – 486 т.р. 4 год – 550 т.р.
2 год – 495 т.р. 5 год – 579 т.р.
3 год – 518 т.р.
Вычислить прогноз издержек обращения на 6 год тремя методами:
1) по среднему приросту
т.р.
+ t = 579 + 23,25 * 1 = 602,25 т.р.
2)по среднему темпу роста
_ _______
T = V 579/486 = 1,045
+ t = 579 * 1.045 = 605 т.р.
3) по уравнению прямолинейной функции
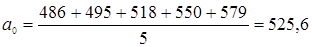т.р.
т.р.
+ t = 525,6 + 24,1 * 3 = 597,9 т.р.
Индексы в статистике
Индекс- это обобщающий относительный показатель, который применяется:
1) для расчета изменений экономического показателя или совокупности показателей за определенный период
2) для расчета отдельных факторов на изменение изучаемых показателей
В зависимости от охвата изучаемых явлений индексы делятся на 2 вида:
- индивидуальные – характеризуют изменение отдельных единиц изучаемой совокупности (i)
- общие – характеризуют изменение всей совокупности, отдельные единицы которой непосредственно не соизмерены (I)
Основным элементом индивидуальных индексов является индексируемая величина – экономический показатель, изменение которого изучается с помощью индекса:
Индивидуальный индекс = индексируемая величина отчетного периода
индексируемая величина базисного периода
В состав общих индексов, кроме индексируемой величины, входит вес индекса – числовой показатель, одинаковый для числителя и знаменателя общего индекса.
Вес индекса должен быть экономически связан с индексируемой величиной, т.е. произведение индексируемой величины на вес индекса образует определенной экономическое явление, например:
«цена товара» * «количество товара» = стоимость товара
индексируемая вес индекса
величина
Общий индекс = индексируемая величина отчетного периода * вес индекса
индексируемая величина базисного периода * вес индекса
Основные виды индексов в статистике торговли:
- индексы цен
- индексы количества проданных товаров (физического объема т/о)
- индексы т/о
1) индексы цен
индивидуальный индекс: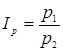 
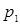– цена отчетного периода
– цена базисного периода
общий индекс: 
* 
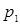– т/о отчетного периода
* – т/о отчетного периода в ценах базисного периода
– количество проданных товаров отчетного периода
индекс цен – индекс качественного показателя. Индексируемая величина – цена товара. Вес индекса – количество проданных товаров отчетного периода. Умножив цену товара на его количество, получаем стоимость проданных товаров, т.е. т/о – величину соизмеримую для всех товаров, имеющих разные натуральные измерители.
Свойство общего индекса цен позволяет вычислить следующие показатели:
1) средний % изменения цен: 
(в %) = 100%
2) абсолютное изменение т/о за счет изменения цен
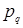(p) = 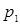(числитель )- (знаменатель )
2) индексы количества проданных товаров
индивидуальный индекс: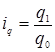 
- количество проданных товаров в отчетном периоде
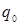- количество проданных товаров в базисном периоде
общий индекс = 
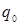* – т/о отчетного периода в цена базисного периода
* – т/о базисного периода
Индекс физического объема т/о – индекс количественного показателя. Индексируемая величина – количество проданных товаров в натуральном измерении. Вес индекса – цена базисного периода. Умножив несоизмеримые количества разнородных товаров на их цену, можно перейти к стоимости товаров, которая является величиной соизмеримой.
Свойство общего индекса количества проданных товаров дают возможность вычислить следующие показатели:
1) средний % изменения количества проданных товаров
Iq (в %) = 100%
2) абсолютное изменение т/о за счет изменения количества проданных товаров
2) индексы товарооборота:
индивидуальный индекс: 
p1 * q1 – т/о отчетного периода по отдельному товару
p0 * q0 – т/о базисного периода по отдельному товару
общий индекс: 
p1 * q1 – т/о отчетного периода
p0 * q0 – т/о базисного периода
1) средний % изменения т/о
Iq (в %) = 100%
2) абсолютное изменение т/о
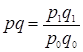
Взаимосвязь индексов:
Отражает взаимосвязь экономических показателей:
Цена * количество = стоимость
Индекс цен * индекс количества проданных товаров = индекс т/о
Ip * Iq = Ipq
pqp= pqp+ pqp
Задачи на тему «Индексный метод»
Условие:
В таблице представлены данные о выпуске продукции и цене за штуку. Рассчитать индивидуальные и общие индексы цен, физического объема и стоимости. Определить общее изменение стоимости продукции в текущем периоде по сравнению с базисным, а так же изменение стоимости за счет уменьшения цен и объема.
Таблица № 17
Выпуск продукции в текущем и базисном периоде
| Вид Продукции | Базисный период | Расчетный период | ||
| Количество, шт | Цена, руб | Количество, шт | Цена, руб | |
| А | ||||
| Б | ||||
| В | ||||
| Г |
| iq=ql/qO ip=pl/pO |
Пример решения для варианта 1
Индивидуальный индекс физического объема рассчитывается по формуле:
Индивидуальный индекс цены рассчитывается по формуле:
Индивидуальный индекс стоимости рассчитывается по формуле: iqp=(qlpl)/(qOpO)
Здесь
qO - объем выпуска продукции в базисном периоде
ql - объем выпуска продукции в текущем периоде
рО - цена единицы продукции в базисном периоде
pi - цена единицы продукции в текущем периоде
Результаты расчетов приведены в таблице
Таблица № 18
Расчет индивидуальных индексов
| Вид про-дукции | Базисный период | Текущий период | Индивидуальные индексы | ||||
| Объем | Цена | Объем | Цена | Объем | Цена | Стоимость | |
| q0 | Р0 | q1 | Р1 | P0q0 | pOql | p1q1 | |
| А | |||||||
| Б | |||||||
| В | |||||||
| Сумма |
Общий индекс стоимости рассчитывается по формуле:
Следовательно, общий индекс цен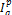 
=14000/10900=1.28 Общий индекс физического объема 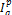=10900/8450=1.29
Общий индекс стоимости 
= 14000/8450= 1.66
Общее изменение стоимости продукции в текущем периоде по сравнению с базисным определяется по формуле
Изменение стоимости продукции в текущем периоде по сравнению с базисным за счет изменения цен на отдельные
виды продукции определяется по формуле
Изменение стоимости продукции в текущем периоде по сравнению с базисным за счет изменения количества производимой продукции
То есть общее изменение стоимости продукции (5550руб) произошло за счет изменения цен(3100руб) и изменения объема(2450руб)
