На Рис. 6. приведены две возможные декомпозиции отношения СЛУЖАЩИЕ_ПРОЕКТЫ
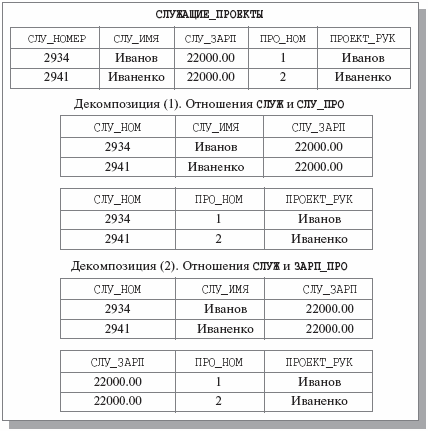
Рис. 6. Две возможные декомпозиции отношения СЛУЖАЩИЕ_ПРОЕКТЫ
Анализ Рис. 6. показывает, что в случае декомпозиции (1) мы не потеряли информацию о служащих – про каждого из них можно узнать имя, размер зарплаты, номер выполняемого проекта и имя руководителя проекта. Вторая декомпозиция не дает возможности получить данные о проекте служащего, поскольку Иванов и Иваненко получают одинаковую зарплату, следовательно, эта декомпозиция приводит к потере информации. Что же привело к тому, что одна декомпозиция является декомпозицией без потерь, а вторая – нет?
Заметим, что при проведении декомпозиции мы использовали операцию взятия проекции. Каждое из отношений СЛУЖ, СЛУ_ПРО и ЗАРП_ПРО является проекцией исходного отношения СЛУЖАЩИЕ_ПРОЕКТЫ. В случае декомпозиции (1) отсутствие потери информации означает, что в результате естественного соединения отношений СЛУЖ и СЛУ_ПРО мы гарантированно получим отношение, заголовок и тело которого совпадают с заголовком и телом отношения СЛУЖАЩИЕ_ПРОЕКТЫ. Следует отметить, что это произойдет для любых допустимых (и согласованных) значений переменных отношений СЛУЖАЩИЕ_ПРОЕКТЫ, СЛУЖ и СЛУ_ПРО, поскольку у всех этих переменных атрибут СЛУ_НОМ является возможным ключом. Однако если выполнить естественное соединение отношений СЛУ и ЗАРП_ПРО, то будет получено отношение, показанное на Рис. 7.
Схема этого отношения, естественно (поскольку соединение – естественное), совпадает со схемой отношения СЛУЖАЩИЕ_ПРОЕКТЫ, но в теле появились лишние кортежи, наличие которых и приводит к утрате исходной информации. Интуитивно понятно, что это происходит потому, что в отношении ЗАРП_ПРО отсутствуют функциональные зависимости СЛУ_ЗАРП 
ПРО_НОМ и СЛУ_ЗАРП ПРОЕКТ_РУК, но точнее причину потери информации в данном случае мы объясним несколько позже.
Корректность же декомпозиции 1 следует из теоремы Хеза:
Теорема Хеза.
Пусть задано отношение r {A, B, C} (A, B и C, в общем случае, являются составными атрибутами) и выполняется FD A B.
Рис. 7. Результат естественного соединения отношений СЛУЖ и ЗАРП_ПРО
Тогда r = (r PROJECT {A, B}) NATURAL JOIN (r PROJECT {A, C}).
Для иллюстрации общего случая применения теоремы Хеза рассмотрим отношение СЛУЖАЩИЕ_ОТДЕЛЫ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ОТД, ПРО_НОМ} (Рис. 8). Атрибут СЛУ_ОТД содержит номера отделов, в которых работают служащие, а ПРО_НОМ – номера проектов, в которых служащие принимают участие. Каждый служащий работает только в одном отделе, т. е. имеется FD СЛУ_НОМ СЛУ_ОТД, но один служащий может участвовать в нескольких проектах.
Рис. 8. Декомпозиция без потерь по теореме Хеза
В отношении СЛУЖАЩИЕ_ОТДЕЛЫ_ПРОЕКТЫ атрибут СЛУ_НОМ не является возможным ключом, но, как показано на Рис. 8, наличия FD СЛУ_НОМ СЛУ_ОТД оказывается достаточно для декомпозиции этого отношения без потерь.
