СТАТИСТИЧНА ФІЗИКА

Розділ 11
ВИХІДНІ ПОЛОЖЕННЯ І ОСНОВНІ РІВНЯННЯ
КЛАСИЧНОЇ СТАТИСТИЧНОЇ ФІЗИКИ
Теоретичні відомості
Статистична фізика, як і термодинаміка, вивчає закономірності теплового руху матерії. Причому руху, який виникає в системах з достатньо великою кількістю частинок N. Як правило, N порівнюють з числом Авогадро NA ≈ 6,022∙1023 моль–1.
Статистична фізика являє собою мікроскопічну теорію багаточастинкових систем довільної природи (атоми, молекули, електрони, іони, фотони, фонони і таке інше). Ця теорія має на меті пояснити макроскопічні властивості таких систем на основі законів руху частинок, з яких вона складається. Тому розрізняють класичну статистичну фізику і квантову статистичну фізику. Спочатку розглянемо класичний підхід, оснований на законах ньютонової механіки.
Отже, завдання координат і імпульсів усіх частинок системи в довільний момент часу визначатиме механічний стан цієї системи. Такий стан в статистичній фізиці називається мікростаном. Сукупний рух частинок (тепловий рух) характеризується макроскопічними параметрами (об’єм, тиск, ентропія, …), які хоча й залежать від координат і імпульсів частинок, але ж однозначно їх не визначають, оскільки кількість таких параметрів << N. Тому при заданих макропараметрах теплового руху можна казати лише про ймовірність того чи іншого мікростану системи. Отже, ймовірнісний опис теплового руху через мікростани зумовлений тим, що мікростан не є адекватним макростану – даний макростан може бути реалізований величезною кількістю різноманітних мікростанів. Як наслідок, для визначення параметрів теплового руху достатньо знання не самих координат та імпульсів частинок, а лише щільності ймовірності мікростану, тобто відносної частоти його появи при еволюції системи з часом. Знаходження щільності ймовірності 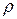 мікростану довільної (класичної чи квантової) системи з наступним визначенням макроскопічних параметрів є основним завданням статистичної фізики.
мікростану довільної (класичної чи квантової) системи з наступним визначенням макроскопічних параметрів є основним завданням статистичної фізики.
Отже, для опису мікростанів класичної системи скористаємося механікою Гамільтона. Нехай система складається з N безструктурних частинок в макрооб’ємі V. Її мікростан у довільний момент часу визначається набором  узагальнених координат та набором
узагальнених координат та набором  узагальнених імпульсів. Зміна мікростану з часом
узагальнених імпульсів. Зміна мікростану з часом  (еволюція системи) визначається рівняннями Гамільтона
(еволюція системи) визначається рівняннями Гамільтона
 (11.1)
(11.1)
з початковими умовами 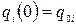 ,
, 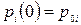 ; тут
; тут
 (11.2)
(11.2)
− функція Гамільтона (повна енергія) системи, m – маса частинки, { А, В } – класична дужка Пуассона:
 . (11.3)
. (11.3)
Геометрично мікростан можна зобразити точкою в умовному 6 N -вимірному  -просторі 3 N узагальнених координат та 3 N узагальнених імпульсів, який називають фазовим простором. Зміна мікростану з часом відповідатиме руху цієї точки у фазовому просторі. Її траєкторія називається фазовою траєкторією.
-просторі 3 N узагальнених координат та 3 N узагальнених імпульсів, який називають фазовим простором. Зміна мікростану з часом відповідатиме руху цієї точки у фазовому просторі. Її траєкторія називається фазовою траєкторією.
Для визначення макроскопічних властивостей в статистичній фізиці уявно розглядають не одну систему, а скільки завгодно велике число макроскопічно ідентичних систем (але з різними мікростанами). Таку сукупність систем називають фазовим ансамблем Гіббса. Якщо тепер зобразити у фазовому просторі точками усі мікростани ансамблю, то саме розподіл цих точок адекватно характеризуватиме макроскопічний стан системи. Такий розподіл математично можна задати через так звану фазову щільність ймовірності 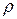 :
:
 , (11.4)
, (11.4)
де 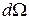 – число точок ансамблю, які попадають у елемент об’єму
– число точок ансамблю, які попадають у елемент об’єму  фазового простору. Вважається, що загальна кількість
фазового простору. Вважається, що загальна кількість 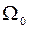 фазових точок прямує до нескінченності. Фазовий ансамбль, в якому стан кожної системи характеризується певною ймовірністю, називається статистичним ансамблем Гіббса.
фазових точок прямує до нескінченності. Фазовий ансамбль, в якому стан кожної системи характеризується певною ймовірністю, називається статистичним ансамблем Гіббса.
Отже, статистичний ансамбль Гіббса задається щільністю ймовірності (або фазовою щільністю) 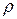 , яка потребує природного нормування на одиницю:
, яка потребує природного нормування на одиницю:
 . (11.5)
. (11.5)
Однак, якщо частинки системи однакові (звичайний випадок), N! можливих переставлень їх місцями мікростанів не змінюватимуть. Уникнення при цьому зайвих точок (які відповідають таким переставленням) ансамблю у фазовому просторі досягається зменшенням щільності 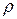 у N! разів. Крім того, щоб величина
у N! разів. Крім того, щоб величина 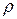 не залежала від вибору одиниць, які використовуються для фазового простору, робиться заміна:
не залежала від вибору одиниць, які використовуються для фазового простору, робиться заміна:  , де h − стала Планка. Така заміна забезпечує також граничний перехід від квантової статистичної фізики до класичної. Отже, “модернізована” умова нормування фазової щільності
, де h − стала Планка. Така заміна забезпечує також граничний перехід від квантової статистичної фізики до класичної. Отже, “модернізована” умова нормування фазової щільності 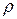 набуває вигляду
набуває вигляду
 , (11.6)
, (11.6)
де  .
.
Знайдемо рівняння для фазової щільності 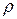 . Фазові точки переміщуються з часом по траєкторіях, які визначаються рівняннями Гамільтона (11.1). При цьому значення
. Фазові точки переміщуються з часом по траєкторіях, які визначаються рівняннями Гамільтона (11.1). При цьому значення 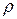 в околі кожної такої точки змінюється зі швидкістю, яка визначається повною похідною за t:
в околі кожної такої точки змінюється зі швидкістю, яка визначається повною похідною за t:
 ; (11.7)
; (11.7)
тут і надалі матимемо на увазі підсумовування за індексом, який повторюється (у кожному одночлені).
При переміщенні фазових точок вони не зникають і не народжуються. Тому для 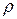 справедливий закон збереження, який виражається рівнянням неперервності
справедливий закон збереження, який виражається рівнянням неперервності
 , (11.8)
, (11.8)
де  – 6 N -вимірний вектор швидкості точки у фазовому просторі. Величина
– 6 N -вимірний вектор швидкості точки у фазовому просторі. Величина  при цьому називається густиною течії ймовірності.
при цьому називається густиною течії ймовірності.
Перепишемо (11.7) у вигляді
 (11.9)
(11.9)
Помітимо, що перші три доданки правої частини (11.9) складають ліву частину (11.8), тобто дорівнюють 0. Отже, з урахуванням (11.1) останню рівність можна записати так:
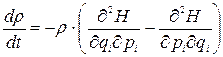 ,
,
звідки випливає фундаментальний результат
 , (11.10)
, (11.10)
який називають теоремою Ліувілля про сталість фазової щільності вздовж фазових траєкторій. (11.10) можна також інтерпретувати як інваріантність елементу фазового об’єму d Г (чи  ) при русі утворюючих його фазових точок.
) при русі утворюючих його фазових точок.
Доведемо останнє твердження. Виділимо в деякий початковий час елемент об’єму 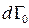 фазового простору. Нехай він містить
фазового простору. Нехай він містить  фазових точок. Тоді можна записати:
фазових точок. Тоді можна записати: 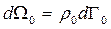 , де
, де  – значення фазової щільності в околі цього об’єму. Через час
– значення фазової щільності в околі цього об’єму. Через час  точки останнього змістяться і займуть деякий об’єм
точки останнього змістяться і займуть деякий об’єм  . Чисельність точок при цьому не зміниться, тобто,
. Чисельність точок при цьому не зміниться, тобто,  , звідки маємо:
, звідки маємо:  . Однак завдяки (11.10) можна вважати
. Однак завдяки (11.10) можна вважати  , що призводить до рівності
, що призводить до рівності  , яку й треба було довести. Враховуючи геометричний зміст якобіанів, згідно з яким можна записати
, яку й треба було довести. Враховуючи геометричний зміст якобіанів, згідно з яким можна записати
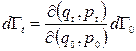 , (11.11)
, (11.11)
бачимо, що виконання теореми Ліувілля еквівалентно рівності
 . (11.12)
. (11.12)
Нагадаємо, що  – якобіан перетворення від змінних
– якобіан перетворення від змінних  (координати та імпульси в початковий момент часу) до змінних
(координати та імпульси в початковий момент часу) до змінних  (координати та імпульси в довільний момент часу
(координати та імпульси в довільний момент часу  ).
).
Перепишемо тепер (11.7) з урахуванням (11.1) та (11.10). Матимемо

або
 , (11.13)
, (11.13)
маючи на увазі антисиметричність дужки Пуассона. Рівняння (11.13) для фазової щільності 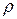 називається рівнянням Ліувілля. Це рівняння лежить в основі статистичного досліджування класичних багаточастинкових систем, тому є основним рівнянням класичної статистичної фізики.
називається рівнянням Ліувілля. Це рівняння лежить в основі статистичного досліджування класичних багаточастинкових систем, тому є основним рівнянням класичної статистичної фізики.
Отже, фазова щільність 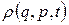 , як і усяка величина, що зберігається з часом, являє собою інтеграл руху. Для більшості фізичних систем існує сім незалежних інтегралів руху: енергія, три проекції повного імпульсу системи та три проекції її моменту імпульсу. Звідси випливає, що щільність ймовірності
, як і усяка величина, що зберігається з часом, являє собою інтеграл руху. Для більшості фізичних систем існує сім незалежних інтегралів руху: енергія, три проекції повного імпульсу системи та три проекції її моменту імпульсу. Звідси випливає, що щільність ймовірності 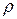 можна розглядати як функцію усіх цих семи змінних. Однак статистична фізика не вивчає ані поступальний, ані обертовий рух системи в цілому. Тому в статистичній фізиці постулюється, що фазова щільність є функцією лише внутрішньої енергії Е:
можна розглядати як функцію усіх цих семи змінних. Однак статистична фізика не вивчає ані поступальний, ані обертовий рух системи в цілому. Тому в статистичній фізиці постулюється, що фазова щільність є функцією лише внутрішньої енергії Е:
 . (11.14)
. (11.14)
Якщо щільність 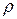 відома, можна вирахувати за цим розподілом середнє значення довільної функції F координат і імпульсів:
відома, можна вирахувати за цим розподілом середнє значення довільної функції F координат і імпульсів:
 . (11.15)
. (11.15)
Така процедура називається статистичним усередненням величини F.
Приклади характерних задач з розв’язанням
Задача 1. Обчислити інтеграли:
а) 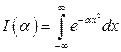 , (
, (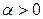 );
);
б)  , (
, ( ;
; 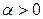 );
);
в)  .
.
Розв’язання. а) Переходячи до інтегрування по площині XOY, запишемо
 . (1)
. (1)
У полярних координатах r,  (враховуючи, що
(враховуючи, що 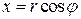 ,
,  ) маємо:
) маємо:  ; при цьому елемент площі
; при цьому елемент площі
 ,
,
де 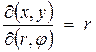 - якобіан переходу від змiнних r,
- якобіан переходу від змiнних r,  до декартових координат x, y. Отже, (1) можна записати у вигляді
до декартових координат x, y. Отже, (1) можна записати у вигляді
 . (2)
. (2)
Обираючи у подвiйному iнтегралi (2) межі iнтегрування так, щоб охопити всю площину XOY, одержимо
 .
.
Отже, остаточно маємо:  .
.
б) У випадку непарних n, зрозуміло,  , тому знайдемо для будь-яких натуральних n iнтеграл
, тому знайдемо для будь-яких натуральних n iнтеграл
 . (3)
. (3)
Замiна  зводить (3) до так званої гамма-функцiї
зводить (3) до так званої гамма-функцiї 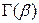 :
:
 ,
, 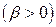 (4)
(4)
з основною властивiстю (довести самостійно)
 . (5)
. (5)
Зокрема, при  та
та  з рівності (4) випливає:
з рівності (4) випливає:  ,
,
 .
.
Використовуючи останні співвідношення, можна визначити  для значень
для значень  . Крім того, враховуючи зв`язок
. Крім того, враховуючи зв`язок  з
з  , знаходимо
, знаходимо
 . (6)
. (6)
Так, з (6) одержуємо:
 ,
,  ,
,  ,
,
 ,
,  ,
, 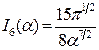 . (7)
. (7)
в) Розглянемо інтеграл
 .
.
Запишемо його у вигляді
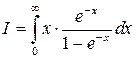 (8)
(8)
Для  величина
величина  являє суму нескінченно спадної прогресії:
являє суму нескінченно спадної прогресії: 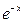 ,
,  ,
,  , …. Отже,
, …. Отже,
 . (9)
. (9)
Послідовність функцій  рівномірно збігається до 0 на проміжку
рівномірно збігається до 0 на проміжку  , тому інтегрування в (9) можна провести під знаком суми:
, тому інтегрування в (9) можна провести під знаком суми:
 .
.
Для визначення цієї суми порівняємо розвинення  в ряд Маклорена із зображенням (за Ейлером) цієї функції як поліному нескінченного степеня з відомими коренями (
в ряд Маклорена із зображенням (за Ейлером) цієї функції як поліному нескінченного степеня з відомими коренями ( ):
):
 .
.
Порівнюючи коефіцієнти при х3, одержимо
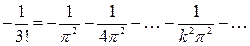
звідки

тобто шуканий інтеграл I дорівнює 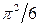 . Аналогічними діями можна довести, що
. Аналогічними діями можна довести, що
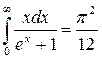 .
.
Задача 2. Ймовірність того, що система знаходиться в стані зі значенням дискретного параметра, дорівнює, де - стала додатна величина,. Пронормувати ймовірність і обчислити середнє значення квадрата і відносну флуктуацію величини (- стала величина).
Розв’язання. З умови нормування

знаходимо:  та
та
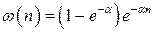 . (1)
. (1)
За ознакою середнього маємо:
 . (2)
. (2)
Суму в (2) можна зобразити у вигляді
 ,
,
що дозволяє обчислити (2) і отримати середнє значення  :
:
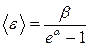 . (3)
. (3)
Аналогічно знаходимо середнє значення величини  :
:
 . (4)
. (4)
Відносну флуктуацію  розраховуємо за формулою
розраховуємо за формулою
 ,
,
що з урахуванням (3) та (4) остаточно дає
 .
.
Задача 3. Математичний маятник здійснює гармонічні коливання за законом. Знайти ймовірність того, що при випадковому вимірюванні кута відхилення маятника це значення буде лежати в інтервалі.
Розв’язання. Ймовірність  того, що при випадковому вимірюванні кута маятника його значення
того, що при випадковому вимірюванні кута маятника його значення  належатиме проміжку
належатиме проміжку  , буде пропорційна часу
, буде пропорційна часу  , протягом якого маятник перебуває (“живе”) в цьому проміжку:
, протягом якого маятник перебуває (“живе”) в цьому проміжку:
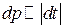 . (1)
. (1)
Із закону коливань маятника знаходимо
 ,
,
звідки
 .
.
Отже, шукану ймовірність (1) можна записати у вигляді
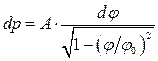 ,
,
де сталу А знаходимо з умови нормування для щільності розподілу  :
:
 ,
,
звідки  і остаточно
і остаточно
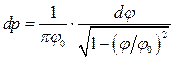 .
.
Задача 4. Ідеальний газ, що складається з 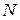 молекул, знаходиться в судині з об’ємом
молекул, знаходиться в судині з об’ємом  . Визначити ймовірність того, що в заданому об’ємі
. Визначити ймовірність того, що в заданому об’ємі  (
( ) у даний момент буде знаходитись рівно
) у даний момент буде знаходитись рівно 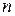 молекул. Розглянути граничні випадки:
молекул. Розглянути граничні випадки:
а)  ;
;
б)  ;
; 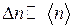 ; (
; ( ).
).
Розв’язання. Випадкове попадання n молекул в об’єм V0 моделюється схемою Бернуллі, де ймовірність попадання однієї молекули в цей об`єм дорівнює 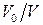 . Тому, якщо вся кількість молекул дорівнює
. Тому, якщо вся кількість молекул дорівнює 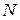 , шукану ймовірність
, шукану ймовірність  можна записати у вигляді
можна записати у вигляді
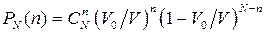 , (1)
, (1)
де  .
.
Розглянемо тепер граничні випадки:
а)  . Позначимо
. Позначимо  . Тоді
. Тоді
 . (2)
. (2)
Оскільки  та
та  , величина
, величина  набуває деякого скінченного сталого значення. Тому після скорочень у (2) одержимо
набуває деякого скінченного сталого значення. Тому після скорочень у (2) одержимо
 .
.
Перша границя дорівнює  , а друга 1. Отже, остаточно у випадку
, а друга 1. Отже, остаточно у випадку  маємо
маємо
 . (3)
. (3)
Розподіл (3) називають розподілом Пуассона. Стала λ має зміст середнього значення кількості молекул 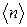 , які попадають в об’єм
, які попадають в об’єм  .
.
б)  ;
; 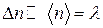 . В цьому випадку користуємося формулою Стірлінга:
. В цьому випадку користуємося формулою Стірлінга:
 . (4)
. (4)
З урахуванням (4) попередній результат (3) після логарифмування матиме вигляд
 . (5)
. (5)
Оскільки  , (5) можна переписати:
, (5) можна переписати:
 . (6)
. (6)
Беручи до уваги розкладання  та враховуючи другий порядок мализни за аргументом
та враховуючи другий порядок мализни за аргументом  , отримаємо
, отримаємо
 , (7)
, (7)
звідки
 . (8)
. (8)
Константу  знаходимо з умови нормування:
знаходимо з умови нормування:
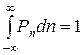 ,
,
що дає:  . Отже, цей випадок призводить до розподілу Гаусса (8).
. Отже, цей випадок призводить до розподілу Гаусса (8).






