Функциональные последовательности и ряды

Математический анализ

Несобственные интегралы

Свойства несобственного интеграла:

1. Для несобственного интеграла справедливы такие арифметические свойства, что и для определенного интеграла.

2. Формула Ньютона-Лейбница: , где .

3. Интегрирование по частям.

4. Замена переменной.

Опр.: Пусть определена на промежутке и интегрируема по Риману на любом отрезке . Несобственным интегралом I-го рода будем называть .

Опр.: Если конечный , то говорят, что сходится. В противном случае говорят, что расходится.

Опр.: называется абсолютно сходящимся, если сходится .

Опр.: Пусть определена и интегрируема на полуинтервале и не ограничена в точке , т.е. , тогда несобственным интегралом .

Теорема (признак сравнения): Пусть и определены и интегрируемы на промежутке и . Если , то: 1) Из сходимости сходимость ; 2) Из расходимости расходимость .

Доказательство: 1) сходится, тогда по теореме (о необходимом и достаточном условии сходимости интегралов) ограничена, т.е. . По условию, , т.е. ограничена, по прошлой теореме сходится. 2) От противного, т.е. предположим, что – сходится, то первому пункту сходится. Противоречие.

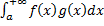Теорема (признак Дирихле): Пусть 1) непрерывна на и имеет ограниченную первообразную на этом промежутке; 2) непрерывна дифференцируема на и монотонно убывает к 0, т.е. . Тогда сходится.

Доказательство: . 1) . 2) Исследуем интеграл от , т.к. . . Из условия – убывающая . Тогда . По признаку сравнения сходится абсолютно.

 

Числовые ряды

Опр.: Выражение вида , где –действительные числа, называется числовым рядом, –общий член ряда.

Опр.: Обозначим . Тогда называется -ой частичной суммой.

Опр.: Если конечный , то говорят, что числовой ряд сходится и его сумма равна .

Опр.: Если не или , то говорят, что числовой ряд расходится.

Теорема (необходимый признак сходимости числового ряда): Если ряд сходится , т.е. это означает, что .

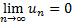Теорема (критерий Коши сходимости числового ряда): Числовой ряд сходится .

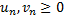Теорема (признак сравнения для рядов с неотрицательными членами): Даны два ряда: и , . Если , то 1) Из сходимости сходимость ; 2) Из расходимости расходимость .

Доказательство: 1) сходится, тогда ограничена, т.е. . Тогда – ограничена ряд сходится. 2) От противного. Если сходится , то из пункта 1 сходится . Противоречие.

Теорема (признак Даламбера): Дан ряд . Если , то при 1) ряд сходится; 2) ряд расходится; 3) – признак Даламбера не даст ответа.

Доказательство: По определению предела последовательности . 1) , возьмём , из . Возьмём , получим и так далее. . Т.к. сходится, то по признаку сравнения сходится и ряд. 2) . Выберем . Из . Берем 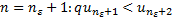и т.д. . расходится ряд расходится.

Теорема (признак Коши): Дан ряд . Если , то при 1) ряд сходится; 2) ряд расходится; 3) –непонятно.

Теорема (интегральный признак сходимости числового ряда): Дан ряд . Если , где - неотрицательная монотонно убывающая функция, то числовой ряд сходится или расходится одновременно с несобственным интегралом.

Доказательство: . , … Сложим всё и получим . Пусть Из , а из сходимости несобственного интеграла ограниченность последовательности . Пусть сходится ряд. Из , т.к. ряд сходится, то ограничена, т.е. . Поэтому интеграл сходится.

 

Знакопеременные ряды

Опр.: Числовой ряд называется абсолютно сходящимся, если сходится ряд .

Опр.: Если ряд абсолютно сходится, то он сходится.

Опр.: Если ряд сходится, но не абсолютно, то он называется условно сходящийся.

Теорема (признак Лейбница для знакочередующихся рядов): Дан ряд . Если последовательность монотонно убывающая и 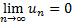, то ряд сходится.

Доказательство: , т.е. монотонно возрастает. 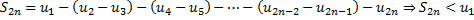, т.е. последовательность ограничена и монотонно возрастает. По теореме Вейерштрасса .

Теорема (признак Дирихле сходимости числовых рядов): Дан ряд . Если последовательность монотонна и и частичные суммы ограничены, то ряд сходится.

Теорема (признак Абеля): Дан ряд . Если 1) последовательность монотонна и ограничена; 2) ряд сходится, то и исходный ряд сходится.

 

Функциональные последовательности и ряды

Свойства:

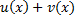1. – непрерывны, то непрерывны.

2. .

3. .

Опр.: Функциональная последовательность – это последовательность, элементами которой являются функции. Обозначается .

Опр.: Функциональный ряд – это выражение вида .

Опр.: Пусть определены на некотором множестве . Будем говорить, что функциональная последовательность сходится в точке , если числовая последовательность – сходится.

Опр.: Будем говорить, что функциональная последовательность сходится на множестве , если она сходится в каждой точке 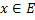. Обозначение .

Опр.: Будем говорить, что функциональный ряд сходится в точке , если сходится числовой ряд и будем говорить, что функциональный ряд сходится на множестве, если он сходится в каждой точке этого множества.

Опр.: Будем говорить, что функциональная последовательность равномерна на множестве сходится к функции , если .

Опр.: Будем говорить, что функциональный ряд сходится равномерно на множестве, если на этом множестве равномерно сходится последовательность частичных сумм.

Опр.: Равномерную сходимость функциональной последовательности можно также записать в виде: .

Опр.: Функциональный ряд сходится равномерно на множестве , если на этом множестве равномерно сходится последовательность его частичных сумм.

Теорема (признак Вейерштрасса равномерной сходимости функциональной последовательности): Дана функциональная последовательность –предельная функция. 1) Если числовая последовательность и и 2) , тогда .

Доказательство: Из второго условия . Переходя к пределу при 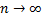и используя теорему о двух полицейских, получим: .

Теорема (признак Вейерштрасса равномерной сходимости функционального ряда): Дан функциональный ряд . Если 1) ; 2) сходится, то функциональный ряд равномерно сходится на множестве .

Доказательство: . Используя критерий Коши для числовых рядов .

Теореме (о непрерывности суммы функционального ряда): Дан функциональный ряд 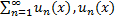непрерывна на . Если функциональный ряд сходится на равномерно, то его сумма непрерывна на .

Доказательство: . Возьмём и рассмотрим разность . Т.к. , то . Т.к. , то , т.к. по условию теоремы непрерывны на , то , непрерывны .

Теорема (о почленном интегрировании функционального ряда): Дан функциональный ряд 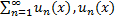непрерывна на . Если функциональный ряд сходится равномерно на , то .

Теорема (о почленном интегрировании функционального ряда): Пусть дан функциональный ряд – непрерывно дифференцируема на . Если 1) сходится равномерно на ; 2) сходится хотя бы в одной точке . Тогда сходится равномерно на .

 

Степенные ряды

Опр.: Степенным рядом называется функциональный ряд вида: , где –центр степенного ряда, –коэффициенты степенного ряда.

Опр.: Число называется радиусом сходимости степенного ряда, если ряд сходится в интервале и расходится вне этого интервала.

Опр.: Если – радиус сходимости, то –интервал сходимости.

Опр.: Функция называется аналитической в точке , если интервал , в котором и ряд сходящийся. Аналитическая функция обладает целым букетом замечательных свойств, в частности она бесконечно дифференцируема. Ещё – единственность разложения в степенной ряд.

Теорема (формула Даламбера для степенного ряда): Дан степенной ряд , то –радиус сходимости.

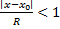Доказательство: Пусть . Применим признак Даламбера сходимости числовых рядов к роду . Если – сходится, – расходится.

Теорема (формула Коши для радиуса сходимости): Если 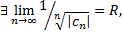то –радиус сходимости.

Теорема (формула Коши-Адамара для радиуса сходимости): Для любого степенного ряда радиус сходимости .