3.1Оформить формат А4(210х297) чертёжной бумаги. На форматевыполнить рамку, но не вычерчивать основную надпись. Написать шрифтом (h=5) в верхней части формата (по центру) наименование схемы алгоритма программы решения математического выражения.
3.2 Выбрать размеры условных графических обозначений символов программы из таблицы «Графические обозначения символов в схемах алгоритмов и программ» (рис.5). В графических заданиях все символы алгоритма программы заданы условно в виде прямоугольников, которые надо заменить на определенные символы по ГОСТ 19.701-90 согласно таблице в правом нижнем углу индивидуального варианта задания.
3.3 Выполнить в тонких линиях компоновку схемы алгоритма программы по центру формата, выбирая расстояния между символами не менее половины высоты символа. Вписать вовнутрь символов необходимые поясняющие надписи чертежным шрифтом (h=5 или h=3.5) по ГОСТ 2.304-81.
3.4 Указать на линиях взаимосвязи стрелки, если направление потока информации отличается от стандартного.
3.5 Обвести изображения символов схемы алгоритма программы решения математического выражения контурными линиями s = 0,7 – 0,8 мм согласно требований ГОСТ 2.303-68.
3.6 Написать чертёжным шрифтом h=5 свою фамилию, инициалы, номер группы и варианта в нижней части формата (по центру).
4 Пример выполнения графической работы «Схема алгоритма программы решения математического выражения» представлен на странице 30 (рис.6), а варианты заданий на странице 15 – 29.
 Рисунок 5 – Графические обозначения символов в схемах алгоритмов и программ
Рисунок 5 – Графические обозначения символов в схемах алгоритмов и программ
Варианты заданий для листа 1
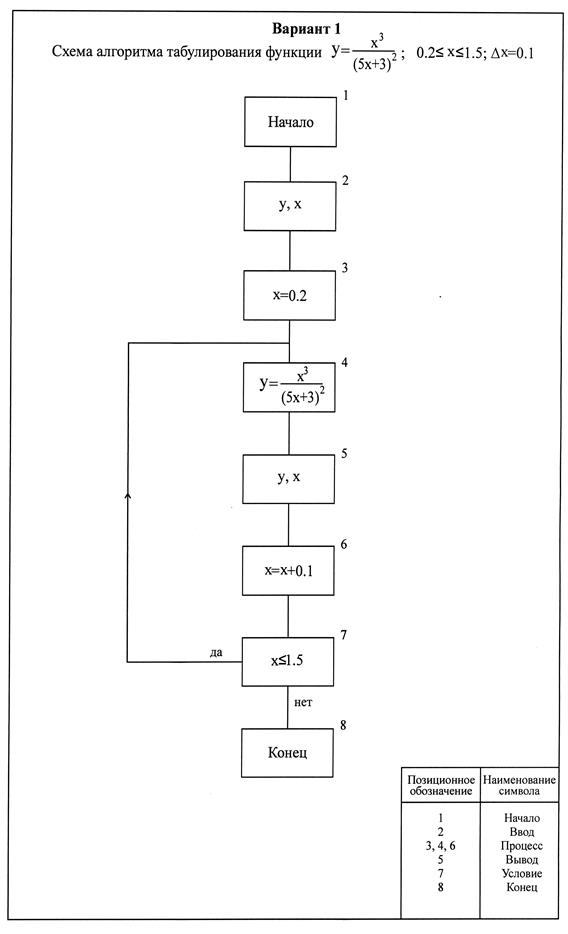





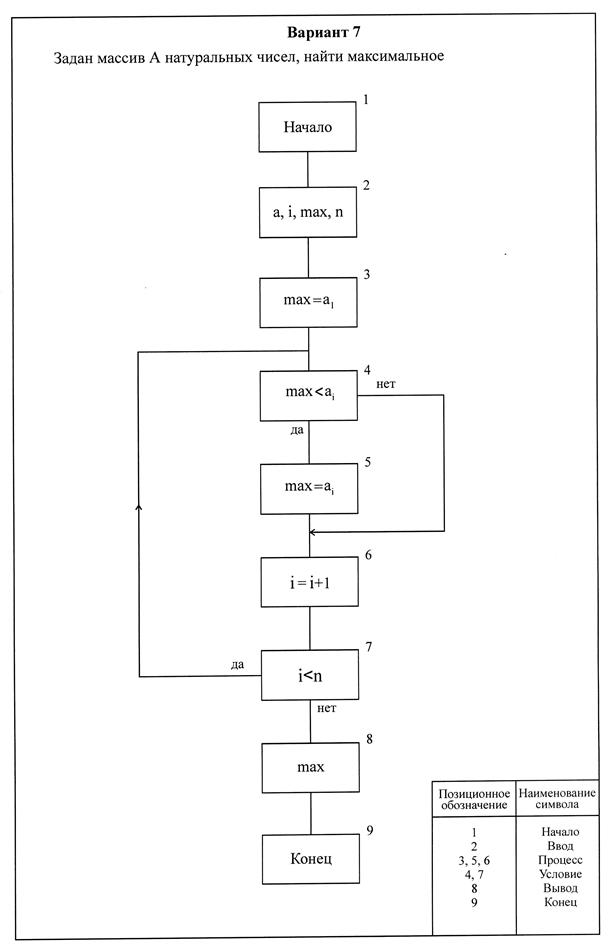


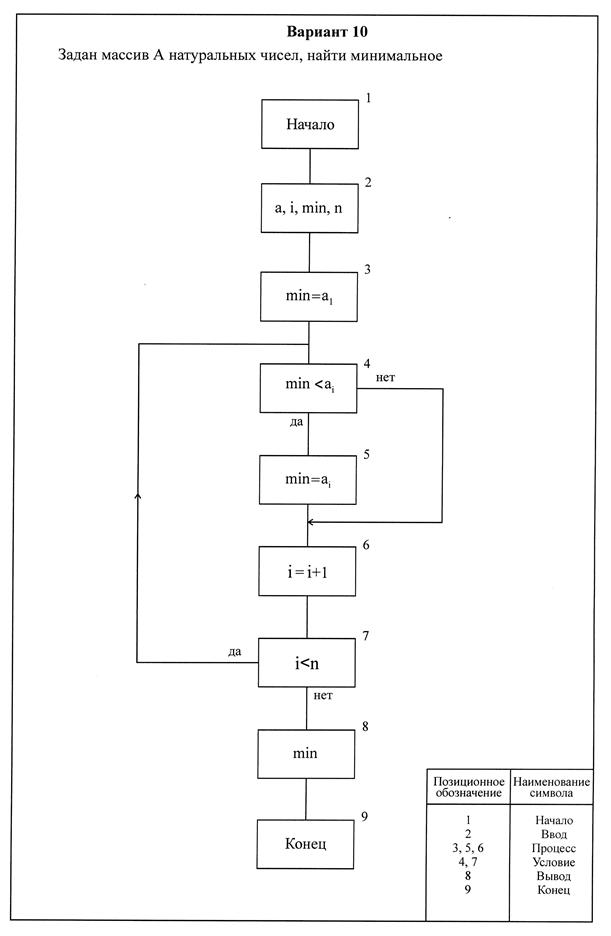
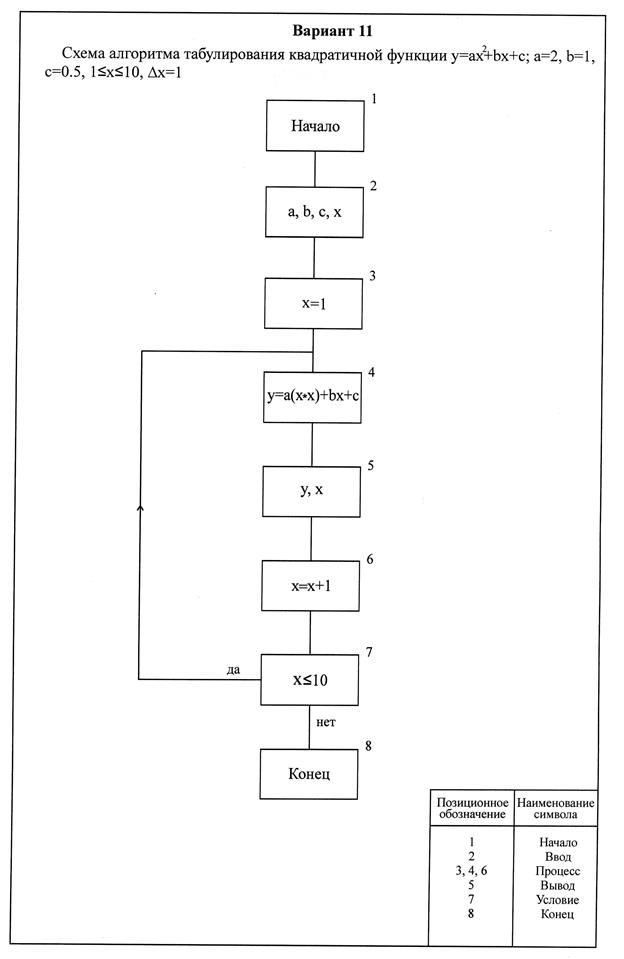
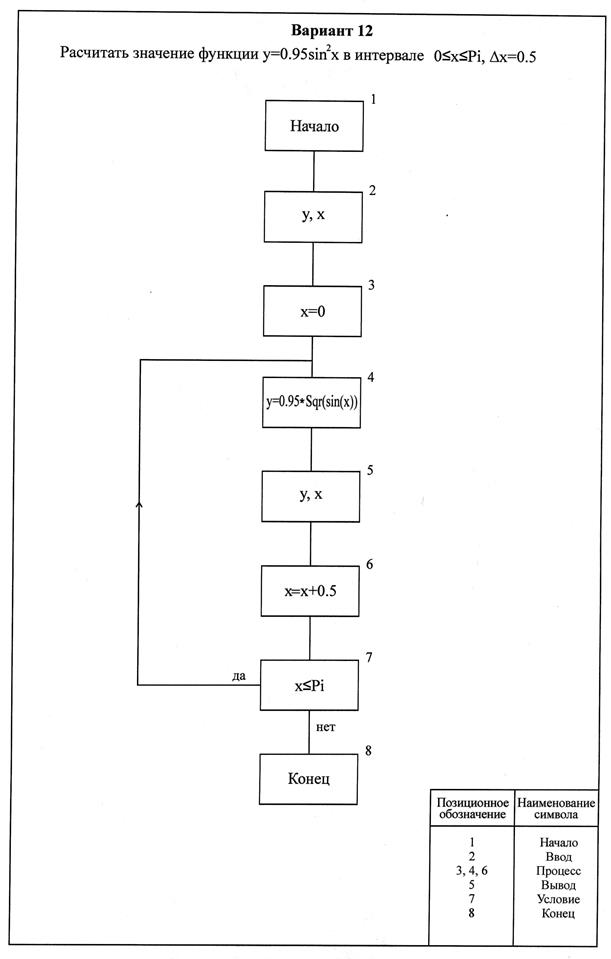




Рисунок 6 - Схема алгоритма программы решения математического выражения
ЛИСТ 2
УСЕЧЕННОЕ ГЕОМЕТРИЧЕСКОЕ ТЕЛО
1 Цель работы:
1.1 Освоить методы определения натуральной величины отрезка прямой и плоскости;
1.2 Изучить методику построения комплексного чертежа усеченного геометрического тела, его развертки и аксонометрии.
Теоретическая часть.
2.1В некоторых случаях на чертежах элементы деталей изображаются в искаженном виде, тогда требуется определить действительную величину этих элементов, например при выполнении чертежей разверток поверхностей геометрических тел. Для определения натуральной величины отрезков и плоских фигур применяются способ вращения и способ перемены плоской проекций.
2.2 Сущность способа вращения заключается в том, что заданная линия или плоская фигура вращается вокруг оси, перпендикулярной к одной из плоскостей проекции. При этом добиваются, чтобы прямая или плоская фигура стали параллельны какой – либо плоскости проекций и таким образом, проецировались в натуральную величину.
2.2.1 Пусть требуется определить способом вращения действительную длину отрезка АВ прямой общего положения, рисунок 7.1(а). Через конец отрезка А проводят ось вращения MN перпендикулярно плоскости Н. Относительно этой оси вращается второй конец отрезка – точка В. Чтобы получить на комплексном чертеже действительную длину отрезка, надо повернуть его так, чтобы он был параллелен плоскости V и тогда фронтальная проекция а/в /, определит действительную длину отрезка АВ, рисунок 7.1(б).
Эту задачу также можно решить вращением отрезка АВ относительно оси, перпендикулярной плоскости V, как показано на рисунке 7.1(в), тогда прямая АВ будет построена параллельно плоскости Н и горизонтальная проекция ав1 будет равна действительной длине отрезка АВ.
2.2.2 Способом вращения можно определить действительный вид плоской фигуры. На рисунке 7.3 изображена стойка поддерживающего ролика ленточного конвейера. Пусть требуется определить действительный вид ребра стойки ролика – прямоугольного треугольника АВС. Как видно из рисунка 7.3 плоскость треугольника горизонтально – проецирующая, поэтому действительный вид треугольника можно получить на плоскости V вращением этого треугольника вокруг вертикальной оси до тех пор, пока плоскость треугольника не станет параллельной плоскости V.
На рисунке 7.3 показан пример определения действительной величины треугольника АВС методом вращения.
2.3 Сущность способа перемены плоской проекции заключается в том, что одна из плоскостей проекции плоскостей заменяется новой, на которую проецируются данная прямая или плоская фигура. При этом, в отличие от предыдущего способа, эти геометрические элементы не меняют своего положения в пространстве.
2.3.1 На рисунке 7.2 изображен пример определения действительной величины отрезка АВ методом перемены плоскостей проекции. В этом случае новая плоскость проекций V1 или Н1 должна быть выбрана так, чтобы она была параллельна отрезку АВ. На рисунке 7.2(а) действительная величина отрезка АВ получается на новой плоскости V1, т. Е. прямая АВ становится фронталью и в1/а1/ - действительная величина отрезка АВ.
На рисунке 7.2(б) построения выполнены так, что прямая АВ становится горизонталью и на новой плоскости Н1 получается а1в1 – действительная величина отрезка АВ.
2.3.2 Действительный вид плоской фигуры так же можно определить способом перемены плоскостей. Для примера возьмем прямоугольный треугольник АВС, который является горизонтально – проецирующим, т.е. перпендикулярным плоскости Н.
В данном примере, на рисунке 7.2(в), плоскость проекций V заменяется новой плоскостью V1, так чтобы новая фронтальная проекция треугольника АВС была его искомым действительным видом.
2.3.3 Подобными приемами построений можно определить действительный вид многоугольника 12345, плоскость которого является фронтально – проецирующей, т.е. перпендикулярной плоскости V как это показано на рисунке 7.4. В этом случае требуется заменить плоскость Н на плоскость Н1, ось проекций которой проводится параллельно фронтальной проекции многоугольника на произвольном расстоянии. На перпендикулярах к оси Х1 откладывают координаты У для точек 1,2,3,4,5 и на плоскости Н1 получают действительную величину многоугольника.
2.4 Изометрическая проекция отрезков и плоских фигур:
2.4.1 В прямоугольной изометрической проекции оси располагаются под углом 1200 друг к другу. Коэффициенты искажения по аксонометрическим осям одинаковы и равны 0,82. Обычно для упрощения построения такого сокращения не делают; отрезки, параллельные аксонометрическим осям, откладывают действительной длины.
2.4.2 Построение изометрической проекции правильного пятиугольника рассматривается на рисунке 8.1. В этом случае для упрощения построения рассматриваются пятиугольники, расположенные на плоскостях проекций H, V и W. Тогда одна из координат вершин пятиугольника будет равна нулю и изометрическую проекцию каждой вершины можно строить по двум координатам. Построив изометрические проекции вершин, соединяем их прямыми линиями и получаем изометрическую проекцию пятиугольника.
|
|
|

|


|
|
|

2.4.3 Изображение в изометрической проекции правильной шестиугольной призмы, выполняют так, как показано на рисунке 8.3. Если основание призмы – правильный шестиугольник, то построение можно упростить, выбрав точку начала координат в центре симметрии многоугольника. Построив изометрическую проекцию основания призмы, из вершины шестиугольника основания проводят прямые, параллельные соответственно осям Х, У или Z (для каждой из рассматриваемых на рисунке 8.3 призм). На этих прямых от вершин основания отложим высоту призмы и получим точки 1, 2, 3, 4, 5, 6 вершин другого основания призмы. Соединив эти точки прямыми линиями, получим изометрическую проекцию призмы. В заключении устанавливаем видимые и невидимые линии; невидимые ребра надо проводить штриховыми линями.
2.4.4 На рисунке 8.2 показана изометрическая проекция куба с окружностями, вписанными в его грани: квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов. Надо запомнить, что малая ось каждого эллипса всегда должна быть перпендикулярна большой оси. При построении изометрической проекции окружности длина большой оси эллипса берется равной 1,22d (диаметра) изображаемой окружности, а длина малой оси эллипса – 0,71d как изображено на рисунке 8.2.
2.4.5 В учебных чертежах вместо эллипсов применяются овалы, очерченные дугами окружности. Упрощенный способ построения овалов приведен на рисунке 8.4. Для построения овала в плоскости Н проводят вертикальную и горизонтальную оси овала как показано на рисунке 8.2(а). Из точки пересечения осей О проводят вспомогательную окружность диаметром d, равным диаметру заданной окружности и находят точки n1, n2, n3 и n4 пересечения этой окружности с осями X и Y. Из точек m1 и m2 , пересечения вспомогательной окружности с аксонометрическими осями X и Y. Из точек m1 и m2, пересечения вспомогательной окружности с осью Z, как из центров радиусом R=m1n4 проводят дуги 23 и 14, принадлежащие овалу. Пересечения этих дуг с осью Z дают точки C и D. Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О1 и О2 . Точки 1, 2, 3 и 4 сопряжений дуг радиусов R и R1 находят, соединяя точки m1 и m2 с точками О1 и О2 и продолжая прямые до пересечения с дугами 23 и 14. Из точек О1 и О2 радиусом R1 = О1 1 проводят две дуги. Так же строят овалы, расположенные в плоскостях V и W, что изображено на рисунке 8.4(б и в).

|
В качестве примера на рисунке 9 приведено построение сечения пятиугольной пирамиды фронтально – проецирующей плоскостью Р, а так же построение аксонометрической проекции и развертки поверхности усеченной пятиугольной пирамиды.
2.4.7 Для построения развертки необходимо знать действительную величину каждого ребра пирамиды. Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку вершину пирамиды и из неё, как из центра, проводят дугу окружности радиусом, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по фронтальной проекции пирамиды, например ребро, на котором находится точка 1. Это ребро пирамиды параллельно плоскости V и проецируется на неё в натуральную величину.
2.4.8 Далее по дуге окружности от любой точки начинают откладывать пять одинаковых отрезков, равных действительной длине стороны пятиугольника – основания пирамиды, которую можно получить на горизонтальной проекции основания пирамиды. Затем на развертке, от основания пирамиды, надо отложить действительную длину каждого из пяти ребер пирамиды. После этого получили развертку боковой поверхности усеченной пирамиды. Теперь к ней нужно добавить основание пирамиды и натуральную величину сечения. Таким образом строится развертка полной поверхности усеченной пирамиды.
2.4.9 Построение изометрической проекции усеченной пирамиды начинают с построения изометрической проекции основания пирамиды, по размерам, взятым с горизонтальной проекции комплексного чертежа. Затем на плоскости основания по координатам точек 1-5 строят горизонтальную проекцию сечения (показана в тонких линиях на изометрии основания). Из вершин полученного пятиугольника проводят вертикальные линии, на которых откладывают координаты высот, взятые с фронтальной проекции. Полученные точки соединяют и получают изометрическую проекцию фигуры сечения. Соединив точки сечения с соответствующими вершинами основания пирамиды, мы получим изометрическую проекцию усеченной пирамиды.


Рисунок 9 – Комплексный чертеж усеченной пирамиды, развертка, изометрия






