Информация. Количество информации. Скорость передачи информации. Скорость телеграфирования

Под термином “ информация ” понимают различные сведения, которые поступают к получателю. В литературе встречается наиболее часто следующее определение информации: информация – это сведения, являющиеся объектом передачи, распределения, преобразования, хранения или непосредственного использования. Это могут быть сведения о результатах измерения, наблюдения за каким-либо объектом и т.п. В дальнейшем нас будут интересовать лишь вопросы, связанные с информацией как объектом передачи.

Сообщение является формой представления информации. Одно и то же сведение может быть представлено в различной форме. Например, сведение о часе приезда вашего приятеля может быть передано по телефону или же в виде телеграммы. В первом случае мы имеем дело с информацией, представленной в непрерывном виде (непрерывное сообщение). Во втором случае – с информацией, представленной в дискретном виде (дискретное сообщение). При передаче сведений по телеграфу информация заложена в буквах, из которых составлены слова, и цифрах. Очевидно, что на конечном отрезке времени число букв или цифр конечное. Это и является отличительной особенностью дискретного или счетного сообщения. В то же время число различных возможных значений звукового давления, измеренное при разговоре, даже на конечном отрезке времени будет бесконечным. В современных цифровых системах телефонной связи в канал связи передаются кодовые комбинации, несущие информацию об отсчетах квантованного аналогового сигнала. Следовательно, такой телефонный квантованный сигнал относится к классу дискретных, и поэтому будем в дальнейшем рассматривать только вопросы передачи дискретных сообщений. В случае телефонной связи под сообщением будем понимать некоторую последовательность отсчетов квантованного аналогового сигнала, передаваемую в канале связи в виде последовательности кодовых комбинаций.

К числу основных информационных характеристик сообщений относятся количество информации в отдельных сообщениях, энтропия и производительность источника сообщений.

Количество информации в сообщении (символе) определяется в битах – единицах измерения количества информации. Чем меньше вероятность появления того или иного сообщения, тем большее количество информации мы извлекаем при его получении. Если в памяти источника имеется два независимых сообщения (а₁ и а₂) и первое из них выдается с вероятностью =1, то сообщение а₁ не несет информации, ибо оно заранее известно получателю.

Было предложено определять количество информации, которое приходится на одно сообщение a_i, выражением

.

С реднее количество информации Н(А), которое приходится на одно сообщение, поступающее от источника без памяти, получим, применив операцию усреднения по всему объему алфавита:

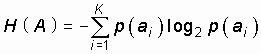. (2.1)

Выражение (2.1) известно как формула Шеннона для энтропии источника дискретных сообщений. Энтропия – мера неопределенности в поведении источника дискретных сообщений. Энтропия равна нулю, если с вероятностью единица источником выдается всегда одно и то же сообщение (в этом случае неопределенность в поведении источника сообщений отсутствует). Энтропия максимальна, если символы источника появляются независимо и с одинаковой вероятностью.

Определим энтропию источника сообщений, если К = 2 и . Тогда

Отсюда 1 бит – это количество информации, которое переносит один символ источника дискретных сообщений в том случае, когда алфавит источника состоит из двух равновероятных символов.

Если в предыдущем примере взять , то Н(А) < 1 бит/сообщ. Таким образом, один бит – максимальное среднее количество информации, которое переносит один символ источника дискретных сообщений в том случае, когда алфавит источника включает два независимых символа.

Среднее количество информации, выдаваемое источником в единицу времени, называют производительностью источника

(бит/с). (2.2)

где Т – среднее время, отводимое на передачу одного символа (сообщения).

Для определения количества единичных элементов, передаваемых в одну секунду ввели понятие скорость модуляции (телеграфирования):

В=1/t (Бод)

Для каналов передачи дискретных сообщений вводят аналогичную характеристику – скорость передачи информации по каналу R (бит/с). Она определяется количеством бит, передаваемых в секунду. Максимально возможное значение скорости передачи информации по каналу называется пропускной способностью канала:

где 2D F – полоса пропускания канала,

Р_с – мощность сигнала,

Р_п – мощность помехи.

Сообщение, поступающее от источника, преобразуется в сигнал, который является его переносчиком в системах электросвязи.

Рис. 2.2. Принцип передачи сообщений

Система электросвязи обеспечивает доставку сигнала из одной точки пространства в другую с заданными качественными показателями. Схема передачи сообщений, в состав которой входят преобразователи сообщение–сигнал–сообщение, приведена на рис. 2.2.

Контрольные вопросы

1. Дайте определения понятиям “информация”, “сообщение”.
2. Как измеряется количество информации?
3. Определить энтропию источника вырабатывающего независимые символы а₁ и а₂, если р(а₁) = 0,3. Сравнить полученное значение с вариантом, когда р(а₁) = р(а₂) = 0,5.

Список литературы

1. Кох Р., Яновский Г. Эволюция и конвергенция в электросвязи. – М.: Радио и связь, 2001. – 280 с.
2. Концепция развития рынка телекоммуникационных услуг Российской Федерации. “СвязьИнформ”, 2001, № 10. с. 9-32.