“”ЌЌ≈Ћ№Ќџ… Ё‘‘≈ “
6.49 ѕотенциальный барьер конечной ширины___________________________________
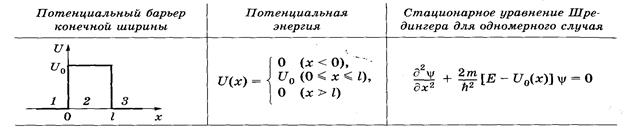
[U0 Ч высота потенциального барьера; ≈ Ч полна€ энерги€ частицы; m Ч масса частицы]
6.50 Ёнерги€ частицы больше высоты потенциального барьера_____________________

[k1,3 =  и k2 =
и k2 =  Ч волновые числа; λ 1, 3 и λ2 Ч соответственно длины волн де Ѕройл€ в област€х 1, 3 и 2]
Ч волновые числа; λ 1, 3 и λ2 Ч соответственно длины волн де Ѕройл€ в област€х 1, 3 и 2]
ќбщие решени€ уравнений Ўредингера ___________________________________________
 ¬ области 3 имеетс€ только прошедша€ барьер волна, поэтому коэффициент ¬3 прин€т равным нулю.
¬ области 3 имеетс€ только прошедша€ барьер волна, поэтому коэффициент ¬3 прин€т равным нулю.
♦  соответствует плоской волне, распростран€ющейс€ в положительном направлении оси х (падающей волне), е -ikxЧ отраженной волне. ќ волнах может идти речь после умножени€ на временной множитель, так как ΨЧ координатна€ часть волновой функции.
соответствует плоской волне, распростран€ющейс€ в положительном направлении оси х (падающей волне), е -ikxЧ отраженной волне. ќ волнах может идти речь после умножени€ на временной множитель, так как ΨЧ координатна€ часть волновой функции.
¬озможное определение коэффициентов отражени€ и прозрачности

¬ывод. ¬ случае ≈ > U 0 волна на границе 1 и 2 частично отражаетс€ ( и частично проходит в область 2, затем она оп€ть на границе 2 и 3 частично отражаетс€ (
и частично проходит в область 2, затем она оп€ть на границе 2 и 3 частично отражаетс€ (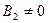 ) и частично проходит в область 3. ¬ облас≠ти 2 (см. рисунок 6.50) длина волны де Ѕройл€ больше, чем в област€х 1 и «.
) и частично проходит в область 3. ¬ облас≠ти 2 (см. рисунок 6.50) длина волны де Ѕройл€ больше, чем в област€х 1 и «.

»так, при E > U0 имеем k1,3 > k2 и λ2 > λ1,3
Ёнерги€ частицы
меньше высоты потенциального барьера (≈ < U 0) _____________________________
”равнение Ўредингера _________________________________________________________

ќбщие решени€ уравнений Ўредингера __________________________________________
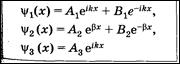 ¬ области 2 решение Ψ2 (х) не соответствует плоским волнам, распростран€ющимс€ в обе стороны (показатели экспонент не мнимые, а действительные).
¬ области 2 решение Ψ2 (х) не соответствует плоским волнам, распростран€ющимс€ в обе стороны (показатели экспонент не мнимые, а действительные).
♦ ¬ области 3 имеетс€ только волна, прошедша€ сквозь барьер и распростран€юща€с€ слева направо, поэтому прин€то ¬3 = 0. »з условий непрерывности волновой функции и ее первой производной в точках х = 0 и х = 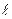 можно найти коэффициенты ј2 и ¬2. ћожно показать, что дл€ высокого и широкого барьера
можно найти коэффициенты ј2 и ¬2. ћожно показать, что дл€ высокого и широкого барьера 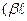 ї1) ¬2ї ј2, а тогда на границе потенциального барьера, где х = 0, опреде л€ющим членом волновой функции Ψ2 €вл€етс€ член, содержащий ¬2
ї1) ¬2ї ј2, а тогда на границе потенциального барьера, где х = 0, опреде л€ющим членом волновой функции Ψ2 €вл€етс€ член, содержащий ¬2  .
.
¬ывод. ¬ случае ≈ < U0, согласно квантовой механике, микрочастица может Ђпройтиї сквозь потенциальный барьер. Ёто специфическое квантовое €вление получило название туннельного эффекта.
6.53 “уннельный эффект________________________________________________________________
¬олновые функции в област€х 1, 2 и 3_________________________________________________

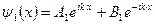
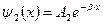

|
| 6.52 |
 ¬ыводы. ¬олнова€ функци€ не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет оп€ть иметь вид волн де Ѕройл€ с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. —ледовательно, частица имеет отличную от нул€ веро€тность прохождени€ сквозь по≠тенциальный барьер конечной ширины Ч наблюдаетс€ туннельный эффект.
¬ыводы. ¬олнова€ функци€ не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет оп€ть иметь вид волн де Ѕройл€ с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. —ледовательно, частица имеет отличную от нул€ веро€тность прохождени€ сквозь по≠тенциальный барьер конечной ширины Ч наблюдаетс€ туннельный эффект.
6.54 оэффициент прозрачности дл€ пр€моугольного барьера______________________
оэффициент прозрачности (веро€тность проникновени€
|
|
|
сквозь потенциальный барьер конечной ширины) ___________________________
 D быстро убывает с увеличением ширины барьера, а также с ростом его высоты.
D быстро убывает с увеличением ширины барьера, а также с ростом его высоты.
[U0 Ч высота потенциального барьера; ≈ Ч энерги€ частицы; 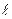 Ч ширина пр€мо≠угольного барьера; т Ч масса частицы;
Ч ширина пр€мо≠угольного барьера; т Ч масса частицы; 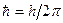 Ч посто€нна€ ѕланка; D 0 Ч по≠сто€нный множитель, который, как показывают точные расчеты, не очень отли≠чаетс€ от единицы]
Ч посто€нна€ ѕланка; D 0 Ч по≠сто€нный множитель, который, как показывают точные расчеты, не очень отли≠чаетс€ от единицы]
6.55 оэффициент прозрачности дл€ барьера произвольной формы____ ___________
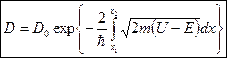

Ёта формула Ч хорошее приближение в случае потенциального барьера произволь≠ной формы, если барьер удовлетвор€ет ус≠ловию квазиклассического приближени€ (достаточно гладка€ форма кривой).
♦ Ёта формула Ч обобщение формулы дл€ D в случае пр€моугольного барьера.
6.56 ¬ыводы относительно поведени€ классической
и квантовой частиц_______________________________________________________
ѕри ≈ < U0 по классической теории частицы не смогут преодолеть потен≠циального барьера и отраз€тс€ от него; согласно квантовой теории, часть частиц отражаетс€, а часть имеет отличную от нул€ веро€тность пройти сквозь потенциальный барьер. ѕри ≈ > U 0,по классической теории все частицы преодолевают потенциальный барьер; согласно квантовой тео≠рии, часть частиц проходит, а часть отражаетс€. ак подбаръерное про≠хождение, так и надбарьерное отражение €вл€ютс€ специфическими квантовыми эффектами, св€занными с волновыми свойствами частиц.






