Вивчення механічного осцилятора з одним ступенем вільності

Лабораторна робота № 1

 

ВИЗНАЧЕННЯ ГОРИЗОНТАЛЬНОЇ СКЛАДОВОЇ ВЕКТОРА МАГНІТНОЇ ІНДУКЦІЇ МАГНІТНОГО ПОЛЯ ЗЕМЛІ

 

Мета роботи: вивчити один з методів визначення горизонтальної складової вектора магнітної індукції магнітного поля Землі.

Прилади та обладнання: тангенс-бусоль, джерело постійної напруги на 4¸6 В, амперметр постійного струму на 0,5¸1А, котушка, реостат на 100¸200 Ом, з’єднувальні дроти, двополюсний перемикач.

 

Методика виконання роботи

Земний магнетизм (геомагнетизм) – магнітне поле Землі та навколоземного космічного простору – зумовлений дією постійних джерел, що містяться всередині Землі і зазнають лише повільних вікових змін, та зовнішніх джерел (змінних), які знаходяться у магніто- й іоносфері. Відповідно розрізняють основне (головне, 99%) і змінне (1%) геомагнітні поля. Складну картину розподілу геомагнітного поля в першому наближенні можна зобразити полем диполя, розташованого в центрі Землі, або однорідною намагніченою кулею, магнітний момент якої спрямований під кутом 11,5° до осі обертання Землі. Геомагнітні полюси Землі не збігаються з географічними. Південний полюс S_M магнітного поля Землі знаходиться біля північних берегів Америки, близько 75° північної широти і 101° західної довготи, а північний полюс N_M – в Антарктиді, близько 67° південної широти і 140° східної довготи.

Для з’ясування походження основного магнітного поля розглядалися різні гіпотези. Сучасні дані про вікові та багаторазові зміни полярності геомагнітного поля задовільно пояснюються тільки моделлю гідромагнітного динамо. Згідно з цією гіпотезою в електропровідному рідкому ядрі Землі проходять дуже складні й інтенсивні рухи, що спричинюють самозбудження магнітного поля, аналогічно тому, як виникає генерація струму й магнітного поля в динамо-машині з самозбудженням. Дія гідромагнітного динамо заснована на явищі електромагнітної індукції в рухомому середовищі, яке під час руху перетинає силові лінії магнітного поля. Дослідження гідромагнітного динамо спираються на магнітну гідродинаміку.

У загальному випадку магнітне поле в ядрі Землі можна уявити у вигляді суми двох складових – тороїдального поля і поля , силові лінії якого лежать в меридіанних площинах.

Схему магнітних полів у гідромагнітному динамо Землі зображено на рис.1, де – поле, близьке до поля диполя, напрямленого вздовж осі обертання Землі; – тороїдальне поле, яке замикається всередині земного ядра. Поле в сотні разів сильніше за проникаюче з ядра назовні поле .

 

Рис. 1

 

У будь-якій точці простору навколо Землі і на поверхні Землі діють магнітні сили. Магнітне поле Землі вивчають за допомогою магнітних вимірювань (магнітна зйомка). Такі вимірювання виконують на суші, в морях та океанах (за допомогою немагнітних суден), у повітрі (аеромагнітні зйомки) і на великих висотах (за допомогою ракет і штучних супутників Землі).

У будь-якому місці земної поверхні вектор магнітної індукції магнітного поля Землі має певне значення та напрямок. Так, біля екватора він спрямований горизонтально, а біля магнітних полюсів – вертикально, в інших точках земної поверхні – під деяким кутом до неї.

Значення величини індукції магнітного поля Землі змінюються від 4,2^.10^-5 Тл на екваторі до 7,0^.10^-5 Тл поблизу магнітних полюсів.

Рис.2

Основними параметрами магнітного поля Землі є магнітне нахилення q (кут між напрямом вектора і площиною горизонту, див. рис.2), магнітне схилення j (кут між горизонтальною складовою вектора та площиною гео

графічного меридіана) і горизонтальна складова індукції магнітного поля Землі .

Географічний меридіан – напрямок, що визначає дійсне положення лінії “північ-південь” у певній місцевості.

Магнітний меридіан – уявна лінія на земній поверхні, що збігається з напрямком земного магнітного поля (напрямок стрілки компаса збігається з напрямком магнітного меридіана).

На магнітних полюсах магнітне нахилення q = ±90°. Тому повна індукція та вертикальна складова магнітного поля мають однакові значення: магнітна стрілка встановлюється у вертикальному положенні.

На магнітному екваторі (q = 0°) повна індукція та горизонтальна складова дорівнюють одна одній: магнітна стрілка встановлюється у горизонтальному положенні.

Напрям вектора досліджують за допомогою магнітної стрілки, яка закріплена на вертикальній осі і може вільно обертатись тільки в горизонтальній площині. Якщо таку магнітну стрілку розмістити у центрі колової рамки зі струмом, розміщеної вертикально в площині магнітного меридіану, то магнітна стрілка встановиться вздовж напрямку вектора магнітної індукції сумарного магнітного поля: магнітного поля Землі (йдеться про горизонтальну складову , оскільки вертикальна складова зрівноважена реакцією опори стрілки) та магнітного поля колової рамки зі струмом індукцією .

Таким чином, остаточно магнітна стрілка встановиться під певним кутом a до напрямку магнітного поля Землі та займе таке положення рівноваги, при якому рівнодіюча цих двох полів буде збігатися з лінією, яка з’єднує полюси стрілки. На рис.3 NS є напрям магнітного меридіана Землі; AB – переріз колової рамки горизонтальною площиною; – вектор горизонтальної складової магнітної індукції магнітного поля Землі; – вектор магнітної індукції магнітного поля, утвореного струмом І в коловій рамці (його напрямок визначається за правилом свердлика).

Кут, під яким встановлюється магнітна стрілка при проходженні струму у коловій рамці, .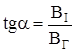

Отже, . (1)

Індукція магнітного поля в центрі одного витка обчислюється за законом Біо-Савара-Лапласа:

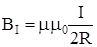, (2)

де m - відносна діелектрична проникність середовища (для повітря m» 1, в той час як для вакууму m=1); m₀ – магнітна стала, m₀= 4p^.10^-7 Гн/м; І – струм у витку; R – радіус витка.

Магнітна індукція в центрі колової рамки зі струмом, що має n витків, дорівнює

. (3)

У даній роботі R = 0,075 м, n = 160 витків.

Підставивши вираз (3) в рівняння (1), отримуємо робочу формулу для обчислення величини горизонтальної складової вектора магнітної індукції магнітного поля Землі:

 

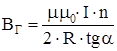(4)

 

Порядок виконання роботи

1. Скласти електричне коло згідно зі схемою, приведеною на рис.4, де E – джерело постійного струму; П – двополюсний перемикач; Б –бусоль; R – реостат; К – колова рамка; А – амперметр постійного струму.

Бусоль БШ-1 складається з магнітної стрілки, закріпленої на проградуйованому лімбі, і оптичної системи, за допомогою якої проводять відлік. Щоб уникнути впливу повітряних течій, магнітна стрілка з лімбом розміщені в металевій коробці, закритій зверху склом. На одному боці коробки розміщена рамка з візирною ниткою, а на протилежному – збираюча лінза в оправі з призмою повного внутрішнього відбивання. Під візирною ниткою розташований аретир. Стрілка, звільнена від аретиру, може вільно обертатися тільки в горизонтальній площині. Спостерігаючи крізь лінзу, одночасно можна бачити поділки шкали (у градусах), нанесені на лімб, і нитку візира під ними.

Після складання електричного кола необхідно звільнити стрілку від аретира і встановити бусоль у площині магнітного меридіана, повертаючи її. При цьому візирна нитка повинна знаходитись проти поділки 90 або 270°, що відповідає напряму схід-захід. При повертанні бусолі треба слідкувати за тим, щоб магнітна стрілка весь час знаходилась у площині витків колового струму, тобто щоб площина витка збігалася з напрямом південь-північ.

2. Відмітити положення візирної нитки за шкалою бусолі (90 або 270°), тобто початок відліку – кут j₀.

3. Замкнути коло. За допомогою реостата встановити силу струму І. Зробити відлік відповідного кута повороту j₁ магнітної стрілки.

4. Перемикачем П змінити напрямок струму І та провести знову відлік відповідного кута j₂ магнітної стрілки. Відлік для двох протилежних напрямків струмів дозволяє уникнути впливу систематичної помилки, пов’язаної з неточністю встановлення колової рамки в площині магнітного меридіану. Знаходимо значення a = çj₁ - j₂÷/2 (де j₁ – кут відхилення праворуч, а j₂ – кут відхилення ліворуч).

5. Провести аналогічні вимірювання при тому самому струмові І п’ять разів. Середнє значення з цих п’яти вимірювань 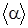використати для обчислення величини B_Г за робочою формулою (4). Всі дані та результати вимірювань занести до таблиці 1.:

Таблиця 1

I= …А; j₀= …; n= 160; R= 0,075 м

№№ п/п	j1 град.	j2, град.	a, град.	Da, град.	(Da)2, град2.	tga	BГ, Тл

< a>= tg< a>= < B_Г >=

 

6. Розрахувати похибки вимірювань і записати результат вимірювання величини горизонтальної складової вектора магнітної індукції магнітного поля Землі.

Кінцевий результат надати у вигляді: В_г = < B_г > ± DВ_г

 

 

Лабораторна робота № 2

 

ВИВЧЕННЯ МЕХАНІЧНОГО ОСЦИЛЯТОРА З ОДНИМ СТУПЕНЕМ ВІЛЬНОСТІ

 

Мета роботи – ознайомитися з характером коливань; розрахувати основні характеристики механічного осцилятора, що зумовлюють процес коливань.

Прилади та обладнання: штатив зі шкалою, пружиною і тягарцем масою m; секундомір; освітлювач.

 

Теоретичні відомості

У механіці найпростішим осцилятором з одним ступенем вільності є пружинний маятник – тіло масою m, що підвішене на невагомій абсолютно пружній пружині довжиною l.

На рис.1 показано тягарець m, підвішений до пружини l, який перебуває у спокої. В цьому положенні на нього діють сили тяжіння () та пружності (). При цьому відповідно до закону Гука, маємо:

 

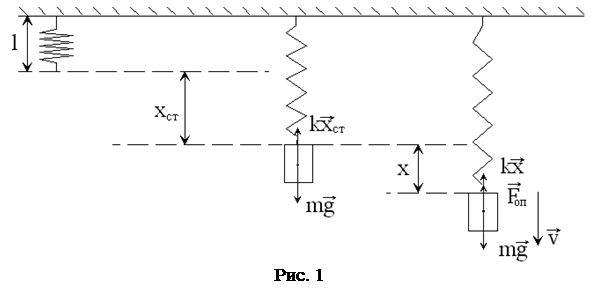
де x_ст – статична деформація пружини.

 

Охарактеризуємо зміщення тіла від стану рівноваги координатою x, причому вісь x спрямуємо вздовж вертикалі вниз, а нуль осі з’єднаємо з положенням рівноваги тіла.

Якщо вивести тіло з положення рівноваги, подовживши пружину на величину x вниз (рис.1) зовнішньою силою, то в пружині виникне додаткова сила пружності , де – вектор зміщення тіла. Якщо після цього припинити дію зовнішньої сили, то в системі пружина–тіло виникне коливний рух. За другим законом Ньютона, маємо:

. (1).

Так як прискорення .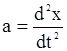

Тоді

.

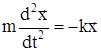Приймемо позначення і отримуємо диференційне рівняння незгасаючих коливань пружинного маятника

(2)

з розв’язком

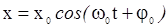, (3)

де x – зміщення тягарця m від положення рівноваги, x₀ – амплітуда коливань, j₀ – початкова фаза.

В реальних умовах при коливаннях необхідно приймати до уваги опір середовища. Для малих швидкостей руху 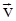сила опору середовища , де r – коефіцієнт опору.

Тоді рівняння руху набуває вигляду:

,

або

 

.

Введемо позначення і дістанемо диференційне рівняння згасаючих коливань пружинного маятника: (4)

з розв’язком

, (5)

де x₀ – початкова амплітуда коливань, – амплітуда згасаючих коливань у момент часу t, e – основа натуральних логарифмів, d – коефіцієнт згасання. Графік цих коливань показаний на рис. 2.

Маса тягарця m, коефіцієнт опору r і жорсткість пружини k називаються параметрами осцилятора (коливальної системи), що розглядається, а величини x₀ і j₀ є константи, які визначаються початковими умовами.

 

Циклічна частота власних коливань маятника (при d=0 – незгасаючі коливання) ,

звідки період власних коливань .

Циклічна частота згасаючих коливань пружинного маятника

.

 

Внаслідок згасання такі коливання не є суворо періодичними. Тому під їх періодом розуміють інтервал часу між двома послідовними максимальними відхиленнями від положення рівноваги в один бік.

 

 

Період згасаючих коливань

.

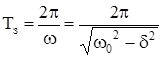Логарифмічний декремент згасання q характеризує згасання (зменшення амплітуди) за один період і визначається як натуральний логарифм відношення двох амплітуд, які рознесені в часі через період T_З

.

Для N коливань .

Часом релаксації t називається проміжок часу, за який амплітуда коливань зменшується в e разів. Оскільки , то dt=1, або 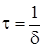, тобто час релаксації t є обернено пропорційний коефіцієнту згасання коливань.

Якщо ввести N_e – число коливань, за яке амплітуда осцилятора зменшується в e разів, то t=T_ЗN_e і логарифмічний декремент згасання

.

Для характеристики коливних систем вводиться поняття добротності системи Q: .

При малих згасаннях (d << w₀) період згасаючих коливань T_З дорівнює періоду власних коливань, тобто T₀, тому

.

Таким чином, чим більша добротність системи, тим повільніше затухають коливання.

Порядок виконання роботи

1. Визначити період коливань T_З . Для цього за допомогою секундоміра виміряти час t, за який тягарець здійснить N₁=20 повних коливань. Визначити період за формулою . Вимірювання повторити не менше п’яти разів і занести до табл. 1. Обчислити похибки. Результати обчислень надати у такому вигляді:

.

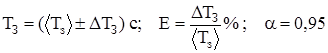Таблиця 1

№№	t, c	Dt, c	(Dt)2, c2	TЗ, с
Середнє знач.

 

2. Визначити логарифмічний декремент згасання q.

Відхилити тягарець від положення рівноваги на 2-3 см, відпустити його, одночасно включивши секундомір, визначити час t, за який амплітуда коливань маятника зменшиться у 2 рази (A₁/A_N=2). Вимірювання повторити три рази і результати занести до табл. 2.

 

Таблиця 2

№№	А1, мм	АN, мм	tN, c	Dt, c	(Dt)2, c2	q
Середзнач.

 

Оскільки безпосередньо визначити положення тягарця відносно шкали важко, то вимірювання краще робити, спостерігаючи рух тіні тягарця вздовж шкали, для чого попередньо треба освітити установку настільною лампою.

Розрахувати логарифмічний декремент згасання:

та похибки вимірювання. Результати надати у такому вигляді:

.

3. Визначити:

а) циклічну частоту згасаючих коливань пружного маятника

;

б) коефіцієнт згасання коливань ;

в) циклічну частоту власних коливань маятника ;

г) час релаксації .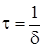

 

 

Лабораторна робота № 3