Метою даного теоретичного вступу було встановлення досить глибокої аналогії між поступальним та обертальним рухами. В табл.1 співставленні основні величини і рівняння поступального руху і обертання навколо нерухомої осі.
Таблиця 2.1
| Поступальний рух | Обертальний рух |
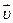 - лінійна швидкість - лінійна швидкість
| 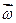 - кутова швидкість - кутова швидкість
|
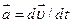 - лінійне прискорення - лінійне прискорення
| 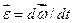 - кутове прискорення - кутове прискорення
|
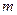 - маса - маса
| 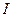 - момент інерції - момент інерції
|
 - імпульс - імпульс
| 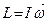 - момент імпульсу - момент імпульсу
|
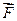 - сила - сила
|  - момент сили - момент сили
|
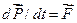 - рівняння динаміки - рівняння динаміки
| 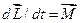 - рівняння динаміки - рівняння динаміки
|
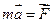 - рівняння динаміки - рівняння динаміки
| 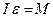 - рівняння динаміки - рівняння динаміки
|
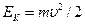 - кінетична енергія - кінетична енергія
| 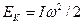 - кінетична енергія - кінетична енергія
|
Із цього співставлення випливає, що відповідають один одному швидкість 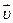 ікутова швидкість
ікутова швидкість 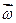 , прискорення
, прискорення 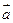 і кутове прискорення
і кутове прискорення  . Роль маси т відіграємомент інерції
. Роль маси т відіграємомент інерції 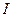 , роль імпульсу
, роль імпульсу 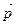 – момент імпульсу
– момент імпульсу 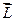 , сили
, сили 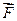 – момент сили
– момент сили  . Отже, основні рівняння поступального і обертального рухів співпадають по формі.
. Отже, основні рівняння поступального і обертального рухів співпадають по формі.
Опис лабораторної установки
Маятник Обербека складається з чотирьох стержнів, закріплених на втулці під прямим кутом один до одного (рис. 2.10).
Втулка з шківом радіуса 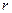 насаджена на вісь в підшипниках так, що вся система може обертатися навколо горизонтальної осі. Момент інерції приладу можна змінювати, пересуваючи тягарці
насаджена на вісь в підшипниках так, що вся система може обертатися навколо горизонтальної осі. Момент інерції приладу можна змінювати, пересуваючи тягарці 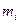 вздовж стержнів. На шків намотана тонка нитка. Прив'язана до неї платформа т служить для розміщення вантажів.
вздовж стержнів. На шків намотана тонка нитка. Прив'язана до неї платформа т служить для розміщення вантажів.
Основний закон динаміки для обертальної системи має вигляд:
 ,
,
де М - сумарний момент сил, діючий на обертальну систему; 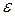 - кутове прискорення системи;
- кутове прискорення системи;  - момент інерції обертальної системи.
- момент інерції обертальної системи.

Рис.2.10
Обертаючий момент створюється силою натягу нитки Т:

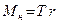 ,
,
де 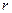 - радіус шківа. Силу Т можна знайти з рівняння руху платформи з вантажами:
- радіус шківа. Силу Т можна знайти з рівняння руху платформи з вантажами:
.
Тут т - маса платформи з вантажами; а - прискорення платформи;  - прискорення вільного падіння.
- прискорення вільного падіння.
Звідси знаходимо:
 .
.
В підшипниках, які забезпечують обертання, діє момент тертя Мтр, прикладений також до осі обертання маятника і направлений протилежно обертальному моменту Мн.. Тому, в загальному випадку,
М = Мн-Мтр.
Однак момент тертя Мтр малий в порівнянні з моментом сили натягу нитки Мн (у лабораторній установці використовуються підшипники, у яких Мтр = 0,01Мн). Отже, при виведенні розрахункових формул дією цього моменту будемо нехтувати, вважаючи, що М = Мн.
Вимірюючи час 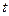 , протягом якого навантажена платформа із стану спокою спускається на відстань
, протягом якого навантажена платформа із стану спокою спускається на відстань  , можна знайти її прискорення
, можна знайти її прискорення 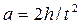 .
.
Нитка тонка і змотується зі шківа маятника без тертя і ковзання, тому лінійне прискорення точок його поверхні також дорівнює а. Кутове прискорення шківа пов'язане з лінійним прискоренням співвідношенням 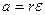 , звідки
, звідки
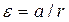 .
.
Основний закон динаміки для даної системи можна записати у вигляді:
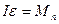 .
.
Підставимо отримані значення 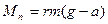 ,
, 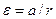 ,
, 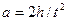 в це рівняння і розв’яжемо його відносно
в це рівняння і розв’яжемо його відносно 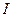 . Дістанемо вираз для моменту інерції системи:
. Дістанемо вираз для моменту інерції системи:

| (3) |
Для визначення моменту інерції 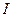 треба знайти дослідним шляхом усі величини, що стоять у правій частині отриманої формули (прискорення вільного падіння
треба знайти дослідним шляхом усі величини, що стоять у правій частині отриманої формули (прискорення вільного падіння 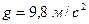 відоме). Тобто необхідно знайти масу платформи з вантажами т, яка приводить систему в рух, радіус шківа
відоме). Тобто необхідно знайти масу платформи з вантажами т, яка приводить систему в рух, радіус шківа 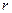 , час
, час 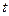 опускання маси т від верхньої точки до нижньої, виміряти шлях
опускання маси т від верхньої точки до нижньої, виміряти шлях 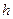 , який платформа проходить при опусканні.
, який платформа проходить при опусканні.
Момент інерції всієї системи складається з моменту інерції 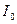 - системи без тягарців
- системи без тягарців 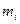 і моменту інерції чотирьох тягарців
і моменту інерції чотирьох тягарців 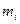 , які закріплені на стержнях.
, які закріплені на стержнях.
В першому наближенні тягарці 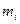 можна прийняти за точкові, тоді момент інерції одного з них можна визначити за формулою:
можна прийняти за точкові, тоді момент інерції одного з них можна визначити за формулою:
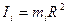 ,
,
де 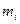 -маса тягарця;
-маса тягарця;
 - віддаль від осі обертання до центра мас тягарця.
- віддаль від осі обертання до центра мас тягарця.
Тоді момент інерції всієї системи можна обчислити за формулою:
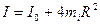
| (4) |
В результаті експерименту, використовуючи формулу (2.1), можна окремо визначити момент інерції 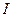 всієї системи, що обертається з масами
всієї системи, що обертається з масами 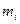 . Потім, знявши маси, аналогічно визначимо момент інерції
. Потім, знявши маси, аналогічно визначимо момент інерції 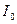 , тобто системи без мас
, тобто системи без мас 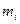 . З виразу (4) знайдемо, що
. З виразу (4) знайдемо, що
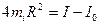
 .
.
Звідки  . Таким чином, момент інерції одного тягарця
. Таким чином, момент інерції одного тягарця 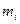 можна визначити експериментально за формулою:
можна визначити експериментально за формулою:
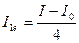 .
.
Тут індекс е означає, що значення отримано експериментально.
Завдання роботи
1. Прийнявши тягарець за матеріальну точку, визначити експериментально момент інерції тягарця і порівняти його з розрахованим за формулою 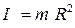 .
.
2. Зробити експериментальну перевірку основного закону динаміки обертального руху  .
.
Виконання роботи
Прилади і матеріали: маятник Обербека; електричні терези ВЛТК-500; лінійка, секундомір, штангенциркуль, набір тягарців, платформа с тягарцями.
1. Визначення моменту інерції тягарця 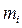
1.1. Визначити окремо маси кожного з чотирьох циліндричних тягарців 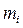 , за допомогою технічних терезів (в лабораторії використовуються терези ВЛТК-500). Знайти середнє значення однієї маси
, за допомогою технічних терезів (в лабораторії використовуються терези ВЛТК-500). Знайти середнє значення однієї маси 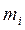 і записати визначене середнє значення до табл. 2.2. Закріпити тягарці
і записати визначене середнє значення до табл. 2.2. Закріпити тягарці 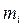 на стержнях на однаковій віддалі
на стержнях на однаковій віддалі  від осі обертання маятника. Треба досягти, щоб маятник знаходився в байдужій рівновазі.
від осі обертання маятника. Треба досягти, щоб маятник знаходився в байдужій рівновазі.
1.2. Визначити відстань R від осі обертання маятника до центрів мас тягарців. Для цього виміряти штангенциркулем довжину тягарця  , діаметр
, діаметр 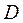 втулки, до якої кріпляться стержні, і відстань
втулки, до якої кріпляться стержні, і відстань 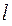 від переднього торця тягарця до поверхні втулки (рис. 2.11). Тоді
від переднього торця тягарця до поверхні втулки (рис. 2.11). Тоді 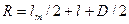 .
.
Виміри зробити для кожного тягарця окремо, знайти середнє значення і записані його до таблиці 2.2.
1.3. Визначити масу т платформи з вантажами.
1.4. Виміряти штангенциркулем радіус шківа 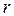 , на який намотана нитка.
, на який намотана нитка.
1.5. Намотати нитку на шків. Платформа з тягарцями буде знаходитися в верхньому положенні. За допомогою лінійки виміряти відстань, з якої буде опускатися платформа.
1.6. Надавши можливості платформі опускатися, по секундоміру визначити час падіння  . Секундомір вмикають у момент початку руху платформи і зупиняють, коли платформа досягає найнижчого положення. Визначити відстань між найнижчим і верхнім положенням платформи
. Секундомір вмикають у момент початку руху платформи і зупиняють, коли платформа досягає найнижчого положення. Визначити відстань між найнижчим і верхнім положенням платформи 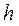 (рис.2.10).
(рис.2.10).
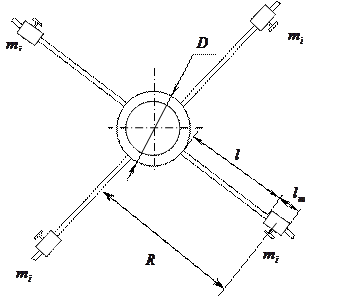 |
Рис. 2.11
1.7. Дослідження повторити три рази. Дані занести до таблиці 2.2 і визначити середні значення.
1.8. За формулою 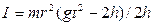 визначити момент інерції
визначити момент інерції 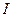 системи з тягарцями.
системи з тягарцями.
1.9. Зняти тягарці 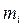 і вище описаним методом визначити момент інерції
і вище описаним методом визначити момент інерції 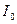 системи без тягарців.
системи без тягарців.
1.10. Визначити експериментальне значення моменту інерції одного тягарця за формулою 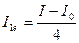 .
.
1.11. Визначити теоретичне значення моменту інерції одного тягарця за формулою  .
.
1.12. Порівняти значення  і
і 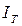 . Для цього визначити відносну похибку вимірювання:
. Для цього визначити відносну похибку вимірювання:
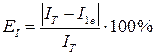 .
.






