Розглянемо послідовність вимірів і обробки результатів вимірювання на конкретному прикладі. Нехай потрібно визначити густину невеликого металевого циліндра (рис.1.3):
 |
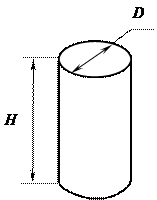Рис. 1.3
Густина матеріалу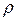 
, з якого виготовлений циліндр, обчислюється за формулою:
,
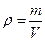де 
- маса, а 
- об’єм циліндра.
Якщо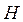 
- висота, а 
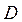- діаметр циліндра, то його об’єм:
.
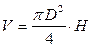Отже, основна розрахункова формула для визначення густини:
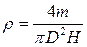. (1)
Послідовність визначення густини може бути наступною.
Виконуються прямі виміри маси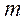 
, діаметра 
і висоти циліндра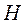 
за методикою, розглянутою в 1.2. Наприклад, маса вимірюється 3-5 разів за допомогою терезів. За результатами вимірювань і подальшої їх обробки отримують значення маси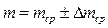 
, де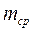 
- середнє значення маси, а 
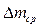- середня абсолютна похибка визначення маси.
Використовуючи штангенциркуль (або мікрометр) аналогічно проводять вимірювання і отримують значення діаметра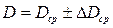 
і висоти 
, де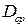 
, 
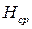- відповідні середні значення, а 
і 
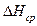- відповідні середні абсолютні похибки.
Після цього починають послідовність обрахунків густини і відповідних похибок, яку називають обробкою результатів при непрямих вимірах.
1. За розрахунковою формулою визначається середнє значення густини:
.
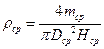2. Слід звернути увагу, що в формулу для непрямого визначення густини підставляються величини, що знайдені при прямих вимірах (
). Тому похибка непрямого виміру повинна знаходитися через похибки прямих вимірів.
Використовуючи математичний апарат диференціального обчислення, можна показати, що при непрямих вимірах зручніше спочатку знайти відносну похибку: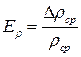 
, а потім обчислити середню абсолютну похибку 
.
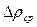Виявляється, що відносна похибка 
результату дорівнює повному диференціалу натурального логарифма функції, яка визначає залежність даної величини від виміряних величин.
Тому відносну похибку слід обчислювати в такій послідовності:
а) прологарифмувати розрахункову формулу:
.
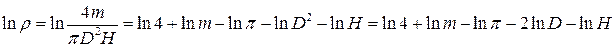б) знайти повний диференціал логарифма 
:
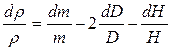. (2)
в) диференціали в отриманому виразі замінити середніми абсолютними похибками: 
, 
, 
, а величини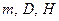 
середніми значеннями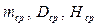 
В самому несприятливому випадку всі похибки виміряних величин відхиляються в один бік. При цьому результуюча похибка стає найбільшою з можливих. Хоча це і малоймовірний випадок, але надійність результату буде максимальною. Тому знаки «–» у формулі (2) замінюємо на «+».
Враховуючи вище сказане, найбільшу відносну похибку вимірювання густини можна знайти за формулою:
.
3) Середню абсолютну похибку можна знайти після обчислення відносної похибки за формулою:
.
4) Результат вимірювання записується у вигляді:
, 
.
Запис результатів
Дуже важливо вміти правильно записувати результати вимірювань, оскільки кінцевий запис несе інформацію як про саму фізичну величину так і про точність з якою вона виміряна. Наприклад, запис результату вимірювання маси m=(0,826±0,003)г означає, що в результаті вимірювання маси тіла знайдене значення 0,826 г з абсолютною похибкою 0,003 г.
Слід підкреслити, що спочатку треба визначити і записати похибку вимірювання, а лише потім записати значення величини, що вимірюється.
При запису похибки слід заокруглювати її величину до двох значущих цифр, якщо перша з них є одиниця, і до однієї значущої цифри в усіх інших випадках.
Наприклад, правильно писати ±3; ±0,2; ±0,08; ±0,14; не слід писати ±3,2; ±0,23; ±0,081; ±0,143. Не слід також заокруглювати ±0,14 до ±0,1.
При запису середнього значення після коми залишається стільки цифр, скільки їх використано при запису похибки.
Наприклад, той самий результат, в залежності від похибки записується у вигляді: 1,2±0,3; 1,27±0,04; 1,271±0,012.
