1. 
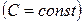
2.  , а Ц любое число
, а Ц любое число
3.  , в частности
, в частности 
4.  , в частности, при
, в частности, при  :
: 
5. 
6. 
7. 
8. 
9. 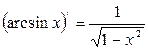
10. 
11. 
12. 
≈сли функции  и
и  дифференцируемы в точке х, то:
дифференцируемы в точке х, то:
- »х сумма дифференцируема в точке х и  (теорема о дифференцировании суммы);
(теорема о дифференцировании суммы);
- ѕроизведение функций  и
и  дифференцируемо в точке х и
дифференцируемо в точке х и  (теорема о дифференцировании произведени€);
(теорема о дифференцировании произведени€);
- „астное функций  и
и  дифференцируемо в точке х, если
дифференцируемо в точке х, если  , и
, и  (теорема о дифференцировании частного).
(теорема о дифференцировании частного).
ѕервообразна€ и интеграл
ѕусть на интервале (а, b) задана непрерывна€ функци€ f(х). ѕо определению функци€ F(х) называетс€ первообразной функцией дл€ f(х) на интервале (а, b), если на нем производна€ от F(х) равна f(х):

ќчевидно, что если функци€  - первообразна€ дл€ f(х) на (а,b), а — Ц некотора€ посто€нна€, то функци€
- первообразна€ дл€ f(х) на (а,b), а — Ц некотора€ посто€нна€, то функци€  есть также первообразна€ дл€ f(х), потому, что
есть также первообразна€ дл€ f(х), потому, что
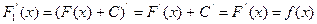
≈сли F(х) кака€-либо первообразна€ от f(х) на интервале (а, b), то возможные первообразные от f(х) на этом интервале выражаютс€ формулой  , где вместо — можно подставить любое число.
, где вместо — можно подставить любое число.
Ќеопределенным интегралом от непрерывной функции f(х) на интервале (а, b) называетс€ произвольна€ ее первообразна€ функци€. Ќеопределенный интеграл обозначаетс€ так:
 .
.
≈сли  ,
,  Ц непрерывные на интервале (а, b) функции и
Ц непрерывные на интервале (а, b) функции и 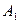 , и
, и  Ц посто€нные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
Ц посто€нные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
 ,
,
где — Ц некотора€ посто€нна€.
—писок основных неопределенных интегралов
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8. 
9. 
10.  ;
;
11. 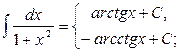
12.  ;
;
13.  ;
;
14. 
«адани€ дл€ контрольной работы по дисциплине
Ђ¬ведениие в физикуї
ќсновы векторной алгебры

1-1. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.

1-2. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.

1-3. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.
 1-4. Ќайдите
1-4. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.

1-5. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.
|
|
|
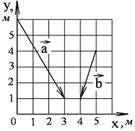
1-6. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.
 1-7. Ќайдите
1-7. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.

1-8. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.

1-9. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.
 1-10. Ќайдите
1-10. Ќайдите
а) модуль суммы 
б) разности 
 двух векторов
двух векторов  и
и  .
.
в) скал€рное произведение векторов  .
. 
г) косинус угла между векторами  и
и 
д) векторное произведение  двух векторов
двух векторов  и
и 
–ешить задачу графически и аналитически.
ѕр€ма€ задача кинематики






