1. «акон —толетова: при неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщени€ пропорционален энергетической освещЄнности катода (иначе: число фотоэлектронов, выбиваемых из катода за 1 с, пр€мо пропорционально интенсивности излучени€):
 и
и 
2. ћаксимальна€ начальна€ скорость фотоэлектронов не зависит от интенсивности падающего света, а определ€етс€ только его частотой.
3. ƒл€ каждого вещества существует красна€ граница фотоэффекта, то есть минимальна€ частота света  (завис€ща€ от химической природы вещества и состо€ни€ поверхности), ниже которой фотоэффект невозможен.
(завис€ща€ от химической природы вещества и состо€ни€ поверхности), ниже которой фотоэффект невозможен.
“еори€ ‘аулера [править | править исходный текст]
ќсновные закономерности внешнего фотоэффекта дл€ металлов хорошо описываютс€ теорией ‘аулера[2]. —огласно ей, после поглощени€ в металле фотона его энерги€ переходит электронам проводимости, в результате чего электронный газ в металле состоит из смеси газов с нормальным распределением ‘ерми Ч ƒирака и возбуждЄнным (сдвинутым на  ) распределением по энерги€м. ѕлотность фототока определ€етс€ формулой ‘аулера:
) распределением по энерги€м. ѕлотность фототока определ€етс€ формулой ‘аулера:

где  ,
,  ,
,  Ч посто€нные коэффициенты, завис€щие от свойств облучаемого металла. ‘ормула справедлива при энерги€х возбуждени€ фотоэмиссии, не превышающих значени€ работы выхода металла более чем на несколько электронвольт. “еори€ ‘аулера верна только в случае падени€ света по нормали к поверхности.
Ч посто€нные коэффициенты, завис€щие от свойств облучаемого металла. ‘ормула справедлива при энерги€х возбуждени€ фотоэмиссии, не превышающих значени€ работы выхода металла более чем на несколько электронвольт. “еори€ ‘аулера верна только в случае падени€ света по нормали к поверхности.
вантовый выход [править | править исходный текст]
¬ажной количественной характеристикой фотоэффекта €вл€етс€ квантовый выход Y Ч число эмитированных электронов в расчЄте на один фотон, падающий на поверхность тела. ¬еличина Y определ€етс€ свойствами вещества, состо€нием его поверхности и энергией фотонов. вантовый выход фотоэффекта из металлов в видимой и ближней ”‘-област€х Y < 0,001 электрон/фотон. Ёто св€зано прежде всего с малой глубиной выхода фотоэлектронов, котора€ значительно меньше глубины поглощени€ света в металле. Ѕольшинство фотоэлектронов рассеивает свою энергию до подхода к поверхности и тер€ет возможность выйти в вакуум. ѕри энергии фотонов вблизи порога фотоэффекта большинство фотоэлектронов возбуждаетс€ ниже уровн€ вакуума и не даЄт вклада в фотоэмиссионный ток. роме того, коэффициент отражени€ в видимой и ближней ”‘-област€х велик и лишь мала€ часть излучени€ поглощаетс€ в металле. Ёти ограничени€ частично снимаютс€ в дальней ”‘-области спектра, где Y достигает величины 0,01 электрон/фотон при энергии фотонов E > 10 э¬.
”равнение Ёйнштейна дл€ внешнего фотоэффекта

¬ќѕ–ќ— 27
–абота выхода в фотоэффекте[править | править исходный текст]
–абота выхода во внешнем фотоэффекте - минимальна€ энерги€, необходима€ дл€ удалени€ электрона из вещества под действием света
«аконы фотоэффекта полностью объ€сн€ютс€ с помощью уравнени€ ј.Ёйнштейна:

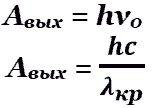 - работа выхода и красна€ граница фотоэффекта (когда Ek = 0).
- работа выхода и красна€ граница фотоэффекта (когда Ek = 0).
Uзe = Ek = mv2/2 - вылетающие при фотоэффекте
электроны можно остановить с помощью отрицательного напр€жени€ между анодом и катодом Uз - з Ђ ра́сна€ї грани́ца фотоэффе́кта Чминимальна€ частота  или максимальна€ длина волны
или максимальна€ длина волны  света, при которой ещЄ возможен внешний фотоэффект, то есть конечна€ кинетическа€ энерги€ фотоэлектронов меньше нул€. „астота
света, при которой ещЄ возможен внешний фотоэффект, то есть конечна€ кинетическа€ энерги€ фотоэлектронов меньше нул€. „астота  зависит только от работы выхода
зависит только от работы выхода 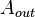 электрона:
электрона:
|
|
|


где 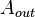 Ч работа выхода дл€ конкретного фотокатода, h Ч посто€нна€ ѕланка, а с Ч скорость света. –абота выхода
Ч работа выхода дл€ конкретного фотокатода, h Ч посто€нна€ ѕланка, а с Ч скорость света. –абота выхода 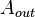 зависит от материала фотокатода и состо€ни€ его поверхности. »спускание фотоэлектронов начинаетс€ сразу же, как только на фотокатод падает свет с частотой
зависит от материала фотокатода и состо€ни€ его поверхности. »спускание фотоэлектронов начинаетс€ сразу же, как только на фотокатод падает свет с частотой  или с длиной волны
или с длиной волны  .
.
адерживающей разностью потенциалов.
¬ќѕ–ќ— 28
‘отоэффект [править | править исходный текст]
ќсновна€ стать€: ‘отоэффект
‘отоэффект Ч это испускание электронов веществом под действием света (и, вообще говор€, любого электромагнитного излучени€). ¬ конденсированных веществах (твЄрдых и жидких) выдел€ют внешний и внутренний фотоэффект.
‘отоэффект был объ€снЄн в 1905 году јльбертом Ёйнштейном (за что в 1921 году он, благодар€ номинации шведского физика ќзеена, получил Ќобелевскую премию) на основе гипотезы ѕланка о квантовой природе света. ¬ работе Ёйнштейна содержалась важна€ нова€ гипотеза Ч если ѕланк предположил, что свет излучаетс€ только квантованными порци€ми, то Ёйнштейн уже считал, что свет и существует только в виде квантованных порций. »з закона сохранени€ энергии, при представлении света в виде частиц (фотонов), следует формула Ёйнштейна дл€ фотоэффекта:

где 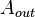 Ч т. н. работа выхода (минимальна€ энерги€, необходима€ дл€ удалени€ электрона из вещества),
Ч т. н. работа выхода (минимальна€ энерги€, необходима€ дл€ удалени€ электрона из вещества),  Ч кинетическа€ энерги€ вылетающего электрона,
Ч кинетическа€ энерги€ вылетающего электрона, 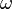 Ч частота падающего фотона с энергией
Ч частота падающего фотона с энергией  ,
,  Ч посто€нна€ ѕланка. »з этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно дл€ того, чтобы Ђвыбитьї электрон из тела. —уть формулы заключаетс€ в том, что энерги€ фотона расходуетс€ на ионизацию атома вещества, то есть на работу, необходимую дл€ Ђвырывани€ї электрона, а остаток переходит в кинетическую энергию электрона.
Ч посто€нна€ ѕланка. »з этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно дл€ того, чтобы Ђвыбитьї электрон из тела. —уть формулы заключаетс€ в том, что энерги€ фотона расходуетс€ на ионизацию атома вещества, то есть на работу, необходимую дл€ Ђвырывани€ї электрона, а остаток переходит в кинетическую энергию электрона.
»спользование законов фотоэффекта [править | править исходный текст]
ѕри данном способе измерени€ посто€нной ѕланка используетс€ закон Ёйнштейна дл€ фотоэффекта:

где  Ч максимальна€ кинетическа€ энерги€ вылетевших с катода фотоэлектронов,
Ч максимальна€ кинетическа€ энерги€ вылетевших с катода фотоэлектронов,
 Ч частота падающего света,
Ч частота падающего света,
 Ч т. н. работа выхода электрона.
Ч т. н. работа выхода электрона.
»змерение проводитс€ так. —начала катод фотоэлемента облучают монохроматическим светом с частотой  , при этом на фотоэлемент подают запирающее напр€жение, так, чтобы ток через фотоэлемент прекратилс€. ѕри этом имеет место следующее соотношение, непосредственно вытекающее из закона Ёйнштейна:
, при этом на фотоэлемент подают запирающее напр€жение, так, чтобы ток через фотоэлемент прекратилс€. ѕри этом имеет место следующее соотношение, непосредственно вытекающее из закона Ёйнштейна:

где  Ч зар€д электрона.
Ч зар€д электрона.
«атем тот же фотоэлемент облучают монохроматическим светом с частотой  и точно также запирают его с помощью напр€жени€
и точно также запирают его с помощью напр€жени€ 
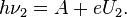
ѕочленно вычита€ второе выражение из первого, получаем

откуда следует

¬ќѕ–ќ— 29
| Ёффект омптона (1923) | |
ј. омптон на опыте подтвердил квантовую теорию света. — точки зрени€ волновой теории световые волны должны рассеиватьс€ на малых частицах без какого-либо изменени€ частоты излучени€, что опытом не подтверждаетс€.
ѕри исследовании законов рассе€ни€ рентгеновских лучей ј. омптон установил, что при прохождении рентгеновских лучей через вещество происходит увеличение длины волны рассе€нного излучени€ по сравнению с длиной волны падающего излучени€. „ем больше угол рассе€ни€, тем больше потери энергии, а следовательно, и уменьшение частоты (увеличение длины волны). ≈сли считать, что пучок рентгеновских лучей состоит из фотонов, которые лет€т со скоростью света, то результаты опытов ј. омптона можно объ€снить следующим образом.
«аконы сохранени€ энергии и импульса дл€ системы фотон - электрон: 
| 
|
| где m0c2- энерги€ неподвижного электрона; hv - энерги€ фотона до столкновени€; hv' - энерги€ фотона после столкно¬≈Ќ»я, P иp' - импульсы фотона до и после столкновени€; mv - импульс электрона после столкновени€ с фотоном. | |
–ешение системы уравнений дл€ энергии и импульса с учетом того, что  дает формулу дл€ измерени€ длины волны при рассе€нии фотона на (неподвижных) электронах: дает формулу дл€ измерени€ длины волны при рассе€нии фотона на (неподвижных) электронах:
| |
 где где  - так называема€ комптоновска€ длина волны. - так называема€ комптоновска€ длина волны.
|
¬ќѕ–ќ— 30
|
|
|
орпускул€рно-волновой дуализм Ц свойство любой микрочастицы обнаруживать признаки частицы (корпускулы) и волны. Ќаиболее €рко корпускул€рно-волновой дуализм про€вл€етс€ у элементарных частиц. Ёлектрон, нейтрон, фотон в одних услови€х ведут себ€ как хорошо локализованные в пространстве материальные объекты (частицы), двигающиес€ с определЄнными энерги€ми и импульсами по классическим траектори€м, а в других Ц как волны, что про€вл€етс€ в их способности к интерференции и дифракции. “ак электромагнитна€ волна, рассеива€сь на свободных электронах, ведЄт себ€ как поток отдельных частиц Ц фотонов, €вл€ющихс€ квантами электромагнитного пол€ ( омптона эффект), причЄм импульс фотона даЄтс€ формулой р = h/λ, где λ Ц длина электромагнитной волны, а h Ц посто€нна€ ѕланка. Ёта формула сама по себе Ц свидетельство дуализма. ¬ ней слева Ц импульс отдельной частицы (фотона), а справа Ц длина волны фотона.
ƒуализм электронов, которые мы привыкли считать частицами, про€вл€етс€ в том, что при отражении от поверхности монокристалла наблюдаетс€ дифракционна€ картина, что €вл€етс€ про€влением волновых свойств электронов. оличественна€ св€зь между корпускул€рными и волновыми характеристиками электрона та же, что и дл€ фотона: р = h/λ (р Ц импульс электрона, а λ Ц его длина волны де Ѕройл€).
орпускул€рно-волновой дуализм лежит в основе квантовой физики.
¬олны де Ѕройл€[править | править исходный текст]
‘изика атомов, молекул и их коллективов, в частности кристаллов, а также атомных €дер и элементарных частиц изучаетс€ в квантовой механике. вантовые эффекты €вл€ютс€ существенными, если характерное значение действи€ (произведение характерной энергии на характерное врем€ или характерного импульса на характерное рассто€ние) становитс€ сравнимым с  (посто€нна€ ѕланка). ≈сли частицы движутс€ со скорост€ми много меньше, чем скорость света в вакууме
(посто€нна€ ѕланка). ≈сли частицы движутс€ со скорост€ми много меньше, чем скорость света в вакууме  , то примен€етс€ нерел€тивистска€ квантова€ механика; при скорост€х близких к
, то примен€етс€ нерел€тивистска€ квантова€ механика; при скорост€х близких к  Ч рел€тивистска€ квантова€ механика.
Ч рел€тивистска€ квантова€ механика.
¬ основе квантовой механики лежат представлени€ ѕланка о дискретном характере изменени€ энергии атомов, Ёйнштейна о фотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определенных услови€х состо€ни€ частиц микромира.
ƒе Ѕройль выдвинул идею о том, что волновой характер распространени€, установленный дл€ фотонов, имеет универсальный характер. ќн должен про€вл€тьс€ дл€ любых частиц, обладающих импульсом  . ¬се частицы, имеющие конечный импульс
. ¬се частицы, имеющие конечный импульс  , обладают волновыми свойствами, в частности, подвержены интерференции и дифракции.
, обладают волновыми свойствами, в частности, подвержены интерференции и дифракции.
‘ормула де Ѕройл€ устанавливает зависимость длины волны  , св€занной с движущейс€ частицей вещества, от импульса
, св€занной с движущейс€ частицей вещества, от импульса  частицы:
частицы:

где  Ч масса частицы,
Ч масса частицы,  Ч ее скорость,
Ч ее скорость,  Ч посто€нна€ ѕланка. ¬олны, о которых идет речь, называютс€ волнами де Ѕройл€.
Ч посто€нна€ ѕланка. ¬олны, о которых идет речь, называютс€ волнами де Ѕройл€.
ƒругой вид формулы де Ѕройл€:

где  Ч волновой вектор, модуль которого
Ч волновой вектор, модуль которого  Ч волновое число Ч есть число длин волн, укладывающихс€ на
Ч волновое число Ч есть число длин волн, укладывающихс€ на  единицах длины,
единицах длины,  Ч единичный вектор в направлении распространени€ волны,
Ч единичный вектор в направлении распространени€ волны,  ƒжЈс.
ƒжЈс.
|
|
|
ƒлина волны де Ѕройл€ дл€ нерел€тивистской частицы с массой  , имеющей кинетическую энергию
, имеющей кинетическую энергию 

¬ частности, дл€ электрона, ускор€ющегос€ в электрическом поле с разностью потенциалов  вольт
вольт

‘ормула де Ѕройл€ экспериментально подтверждаетс€ опытами по рассе€нию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещества. ѕризнаком волнового процесса во всех таких опытах €вл€етс€ дифракционна€ картина распределени€электронов (или других частиц) в приемниках частиц.
¬олновые свойства не про€вл€ютс€ у макроскопических тел. ƒлины волн де Ѕройл€ дл€ таких тел настолько малы, что обнаружение волновых свойств оказываетс€ невозможным. ¬прочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно €рким примером этому служат сверхпроводимость и сверхтекучесть.
‘азова€ скорость волн де Ѕройл€ свободной частицы

где 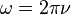 Ч циклическа€ частота,
Ч циклическа€ частота,  Ч кинетическа€ энерги€ свободной частицы,
Ч кинетическа€ энерги€ свободной частицы, 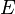 Ч полна€ (рел€тивистска€) энерги€ частицы,
Ч полна€ (рел€тивистска€) энерги€ частицы,  Ч импульс частицы,
Ч импульс частицы,  ,
,  Ч еЄ масса и скорость соответственно,
Ч еЄ масса и скорость соответственно,  Ч длина дебройлевской волны. ѕоследние соотношени€ Ч нерел€тивистское приближение. «ависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. ‘азова€ скорость
Ч длина дебройлевской волны. ѕоследние соотношени€ Ч нерел€тивистское приближение. «ависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. ‘азова€ скорость 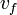 волны де Ѕройл€ хот€ и больше скорости света, но относитс€ к числу величин, принципиально неспособных переносить информацию (€вл€етс€ чисто математическим объектом).
волны де Ѕройл€ хот€ и больше скорости света, но относитс€ к числу величин, принципиально неспособных переносить информацию (€вл€етс€ чисто математическим объектом).
√руппова€ скорость волны де Ѕройл€  равна скорости частицы
равна скорости частицы  :
:
 .
.
—в€зь между энергией частицы 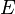 и частотой
и частотой  волны де Ѕройл€
волны де Ѕройл€

¬олны де Ѕройл€ имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модул€ амплитуды волны де Ѕройл€ в данной точке €вл€етс€ мерой веро€тности того, что частица обнаруживаетс€ в этой точке. ƒифракционные картины, которые наблюдаютс€ в опытах, €вл€ютс€ про€влением статистической закономерности, согласно которой частицы попадают в определенные места в приЄмниках Ч туда, где интенсивность волны де Ѕройл€ оказываетс€ наибольшей. „астицы не обнаруживаютс€ в тех местах, где, согласно статистической интерпретации, квадрат модул€ амплитуды Ђволны веро€тностиї обращаетс€ в нуль.






