ќбъем продаж, млн. руб. 
| „исло фирм, 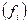
| —ередина
интервала
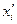
|
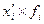
|

|
| - 5 5 - 9 9 - 13 13 - | ||||
| »того | - |
— веро€тностью 0,954 определить:
1) средний объем продаж  ;
;
2) долю фирм, имеющих объем продаж 5 Ц 9 млн. руб. и ниже.
–ешение.
ƒоверительный интервал дл€ генеральной средней  :
:

¬ыборочна€ средн€€:  (млн. руб.).
(млн. руб.).
ѕредельна€ ошибка выборки: 
ѕо условию –(t) = 0,954, t = 2,0 (по таблице значений интеграла Ћапласа).
¬ыборочна€ дисперси€:

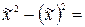
 .
.
—редн€€ ошибка выборки дл€ бесповторного отбора:
 ;
;
 млн. руб.
млн. руб.
ќпределим с веро€тностью 0,954 предельную ошибку выборки:
 млн. руб.
млн. руб.
√раницы генеральной средней:
 ;
;
 .
.
“аким образом, с веро€тностью 0,954 можно утверждать, что средний объем продаж фирм лежит в пределах от 7,56 до 8,44 млн. руб.
ƒолю фирм, имеющий объем продаж 5 Ц 9 млн. руб. и ниже, определим по формуле:

¬ыборочна€ дол€:

—редн€€ ошибка выборки:
 =
=  0,001.
0,001.
ѕредельна€ ошибка выборки с заданной веро€тностью составит:

√раницы генеральной доли:



—ледовательно, с веро€тностью 0,954 можно утверждать, что дол€ фирм, с объемом продаж 5 Ц 9 млн. руб. и ниже, находитс€ в пределах от 68, 8 % до 69,2 %.
ќпределение необходимой численности выборки
ѕри организации выборочного наблюдени€ необходимо правильно определить объем выборки n, который обеспечит требуемую точность результатов с заданной веро€тностью.
–асчет необходимого объема выборки проводитс€ на основе предельной ошибки выборки  в соответствии с видом и методом отбора единиц. Ќапример, выведем формулу объема дл€ средней
в соответствии с видом и методом отбора единиц. Ќапример, выведем формулу объема дл€ средней  при собственно-случайной повторной выборке. »меем,
при собственно-случайной повторной выборке. »меем,


јналогично можно получить остальные формулы расчета оптимального объема выборки в зависимости от вида и метода отбора (табл. 7.5).
“аблица 7.5
‘ормулы определени€ необходимого объема выборки n
(m Ц дл€ серийной) при различных методах отбора
| ћетод отбора | ќцениваемый параметр | ¬ид отбора | |
| повторный | бесповторный | ||
| —обственно-случайный и механический | средн€€ 
| 
| 
|
дол€ 
| 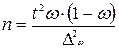
| 
| |
| “ипический (пропорциональный) | средн€€ 
| 
| 
|
дол€ 
| 
| 
| |
| —ерийный | средн€€ 
| 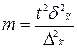
| 
|
дол€ 
| 
| 
|
—ледует помнить, что величина объема выборки не может быть дробной. ѕоэтому в случае дробного ответа объем выборки округл€ют только в  сторону. Ќапример, если получено 42, 25, то объем равен 43, если 54, 82, объем равен 55.
сторону. Ќапример, если получено 42, 25, то объем равен 43, если 54, 82, объем равен 55.
“аким образом, чем больше объем выборки n, тем меньше значени€ предельной ошибки  выборочного наблюдени€. », следовательно, тем уже границы генеральной средней
выборочного наблюдени€. », следовательно, тем уже границы генеральной средней  и генеральной доли
и генеральной доли  . — другой стороны, увеличение численности выборки сопровождаетс€ ростом затрат на проведение наблюдени€. ѕоэтому два этих процесса надо оптимизировать.
. — другой стороны, увеличение численности выборки сопровождаетс€ ростом затрат на проведение наблюдени€. ѕоэтому два этих процесса надо оптимизировать.
≈сли дол€ отбора не превышает 5 %, то формулу бесповторного отбора можно не использовать, так как это существенно не скажетс€ на величине объема n.
|
|
|
ѕри решении задачи определени€ необходимого объема выборки величина допустимой предельной ошибки  и уровень веро€тности, гарантирующей точность оценок выборки, задаютс€ заранее. ј величина генеральной дисперсии
и уровень веро€тности, гарантирующей точность оценок выборки, задаютс€ заранее. ј величина генеральной дисперсии  , как правило, неизвестна.
, как правило, неизвестна.
ƒл€ оценки генеральной дисперсии можно использовать:
1. выборочную дисперсию по данным предшествующих или пробных обследований;
2. дисперсию  , найденную из соотношени€ дл€ среднего квадратического отклонени€:
, найденную из соотношени€ дл€ среднего квадратического отклонени€:

3. дисперсию  , вычисленную из соотношени€ дл€ нормального распределени€:
, вычисленную из соотношени€ дл€ нормального распределени€:  где
где  - размах вариации.
- размах вариации.
4. дисперсию  , определенную из соотношени€ дл€ асимметричного распределени€:
, определенную из соотношени€ дл€ асимметричного распределени€:  где
где  - размах вариации.
- размах вариации.
¬ качестве оценки генеральной дисперсии доли  используют результаты предыдущих исследований или максимально возможное значение дисперсии альтернативного признака
используют результаты предыдущих исследований или максимально возможное значение дисперсии альтернативного признака 
ћала€ выборка
¬ практике статистических исследований часто приходитс€ сталкиватьс€ с малыми выборками, которые имеют объем менее 30 единиц. большим же обычно относ€т выборки объемом свыше 100 единиц.
ќбычно малые выборки примен€ютс€ в случа€х, когда невозможно или нецелесообразно использовать большую выборку. »меть дело с такими выборками приходитс€, например, при опросах туристов и посетителей гостиниц.
¬еличина ошибки малой выборки определ€етс€ по формулам, отличающимс€ от формул дл€ сравнительно большого объема выборки ( ).
).
ѕри малом объеме выборки n следует учитывать взаимосв€зь между выборочной  и генеральной дисперсией
и генеральной дисперсией  :
:

“ак как при малой выборке дробь 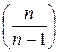 имеет существенное значение, то вычисление дисперсии производитс€ с учетом, так называемого числа степеней свободы
имеет существенное значение, то вычисление дисперсии производитс€ с учетом, так называемого числа степеней свободы  . ќно понимаетс€ как число вариантов
. ќно понимаетс€ как число вариантов  , которые могут принимать произвольные значени€, не мен€€ величины средней
, которые могут принимать произвольные значени€, не мен€€ величины средней  .
.
—редн€€ ошибка малой  выборки определ€етс€ по формуле:
выборки определ€етс€ по формуле:

ѕредельна€ ошибка выборки  дл€ средней и доли находитс€ аналогично случаю большой выборки:
дл€ средней и доли находитс€ аналогично случаю большой выборки:

где t Ц коэффициент довери€, завис€щий от заданного уровн€ значимости  и числа степеней свободы
и числа степеней свободы  (ѕриложение 5).
(ѕриложение 5).
«начени€ коэффициента завис€т не только от заданной доверительной веро€тности  , но и от объема выборки n. ƒл€ отдельных значений t и n доверительна€ веро€тность
, но и от объема выборки n. ƒл€ отдельных значений t и n доверительна€ веро€тность  определ€етс€ по распределению —тьюдента, которое содержит распределени€ стандартизованных отклонений:
определ€етс€ по распределению —тьюдента, которое содержит распределени€ стандартизованных отклонений:
 .
.
«амечание. ѕо мере увеличени€ объема выбор≠ки распределение —тьюдента приближаетс€ к нормальному распределению: при n =20 оно уже мало отличаетс€ от нормального распределе≠ни€. ѕри проведении малых выборочных обследований следует учесть, что чем меньше объем выборки n, тем больше раз≠личие между распределением —тьюдента и нормальным рас≠пределением. Ќапример, при пmin. = 4 это различие весьма существенно, что говорит об уменьшении точности результатов малой выборки.
–аспределение —тьюдента примен€етс€ дл€ решени€ следующих задач малой выборки:
1) оценка средней  и доли
и доли  по малой выборке;
по малой выборке;
2) интервальна€ оценка по малой выборке.






