1. Если главный вектор всех внешних сил системы равен нулю (
), то количество движения системы постоянно по величине и направлению. 
2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю (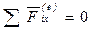
), то проекция количества движения системы на эту ось является постоянной величиной. 
Теорема о движении центра масс.
Теорема Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
, следовательно 
Момент количества движения системы.
Моментом количества движения системы материальных точек 
относительно некоторого центра 
называется векторная сумма моментов количества движения отдельных точек этой системы относительно того же центра 
Моментом количества движения системы материальных точек 
относительно какой-либо оси 
, проходящей через центр , называется проекция вектора количества движения 
на эту ось 
.
Момент количества движения твердого тела относительно оси вращения при вращательном движении твердого тела.
Вычислим момент количества движения твердого тела относительно оси вращения.
Момент количества движения твердого тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения. 
Теорема об изменении момента количества движения системы.
Теорема. Производная по времени от момента количества движения системы, взятого относительно какого-нибудь центра, равна векторной сумме моментов внешних сил, действующих на систему относительно того же центра.
(6.3)
Доказательство: Теорема об изменении момента количества движения для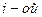 
точки имеет вид:
, 
Сложим все 
уравнений и получим:
или ,
что и требовалось доказать.
Теорема. Производная по времени от момента количества движения системы, взятого относительно какой-либо оси, равна векторной сумме моментов внешних сил, действующих на систему относительно той же оси.
Для доказательства достаточно спроектировать векторное уравнение (6.3) на эту ось. Для оси это будет выглядеть так:.
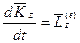(6.4)
Теорема об изменении момента количества движения системы относительно центра масс. (без доказательства)
Для осей движущихся поступательно вместе с центром масс системы, теорема об изменении момента количества движения системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.
