В теоретической механике различают свободную материальную точку, свободную систему и свободное твердое тело, а также несвободную материальную точку, несвободную систему, несвободное твердое тело.
Если на движение материальной точки, системы или твердого тела не наложены наперед заданные ограничения, то материальная точка, система или твердое тело называются свободными.
В противном случае материальная точка, система или твердое тело называются несвободными. Физические условия, ограничивающие свободу движения указанных материальных объектов, называются связями.
В статике встречаются простейшие связи, осуществляемые раз
личными твердыми или гибкими телами.
Сила, с которой связь действует на рассматриваемую точку, систему или твердое тело, называется реакцией связи.
Виды связей и их реакции.
Связью может быть нить, шнур, веревка, цепь, трос и т. д. В теоретической механике принимают, что такие связи являются невесомыми, гибкими и
нерастяжимыми. Реакции этих связей направлены соответственно: по нити, веревке и т. д. В отличие от стержня, здесь Рис. 4 известна не только линия действия реакции, но и ее направление. Реакции нити, веревки и других гибких связей будем обозначать буквой Т.
Однако существуют такие связи, линии действия которых
наперед нельзя указать. К числу таких связей относится, например, неподвижный цилиндрический шарнир.
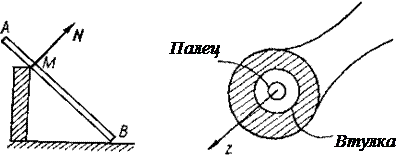
Он состоит из неподвижного цилиндрического болта (пальца), на который надевается втулка (рис.), имеющая цилиндрическое отверстие с диаметром, немного превышающим диаметр болта. Если тело скрепить с втулкой, то оно сможет только вращаться вокруг оси шарнира. В идеальном шарнире, в котором пренебрегают трением между поверхностями пальца и втулки, возникает только препятствие для перемещения втулки в направлении, перпендикулярном к поверхностям пальца и втулки. Поэтому реакция в идеальном шарнире направлена по нормали, т. е. по радиусу болта. В зависимости от действующих сил втулка может прижиматься к болту в любой точке. Поэтому направление реакции неподвижного цилиндрического шарнира наперед указать нельзя. Об этой реакции известно только то, что она расположена в плоскости, перпендикулярной к оси, шарнира. Схематически неподвижный шарнир изображают двумя стержнями, соединенными общим шарниром. При решении задач реакцию шарнира определяют аналитически, раскладывая ее по направлениям координатных осей. Величину проекций реакции определяют из уравнений равновесия. Аналогично поступают и в других случаях, когда направление реакции какой-то связи наперед указать нельзя.
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.
Система сходящихся сил либо приводится к равнодействующей, либо находится в равновесии.
Теорема. Равнодействующая системы сходящихся сил равна векторной сумме этих сил.

Действительно, пусть к абсолютно твердому телу приложена система сил F1, F2,..., Fn, линии действия которых пересекаются в некоторой точке О (рис.). Мы могли бы складывать последовательно эти силы по аксиоме о параллелограмме сил. Однако этот путь очень длинен. Пользуясь правилом геометрического сложения векторов, сразу построим многоугольник сил F1, F2,..., Fn, замыкающая сторона которого и будет равнодействующей силой R.
Изложенный способ определения равнодействующей является геометрическим. Однако равнодействующую силу R можно определить и аналитически, по проекциям на неподвижные оси декартовой системы координат, выбрав за начало координат точку О пересечения линий действия системы сходящихся сил.






