Ћекци€ 17
«онна€ теори€ твЄрдых тел
–ассматрива€ квантовую теорию электропроводности металлов не учитывалось, что положительные ионы кристаллической решЄтки создают в металле электрическое поле и как вообще по€вл€ютс€ электроны проводимости, которые в кристаллах металлов есть, а в кристаллах диэлектриков отсутствуют.
¬ зонной теории твЄрдое кристаллическое тело рассматриваетс€ как строго периодическа€ структура, в которой ионы создают электрическое поле. “очное решение уравнени€ ЎрЄдингера дл€ такой системы множества частиц невозможно, поэтому используют различные упрощающиеприближени€.
ћодель ронигаЦѕенни учитывает движение только внешних электронов в поле периодически расположенных ионных остовов, содержащих €дро атома и электроны внутренних подоболочек. ¬ этом случае удобнее использовать уравнение ЎрЄдингера дл€ электрона, движущегос€ в более слабом поле с потенциалом периодически расположенных ионных остовов. ќднако такой подход позвол€ет решать только одномерные задачи движени€ электронов.
—уществуют ещЄ два метода решени€ задачи, которые привод€т практически к одинаковым результатам.
ѕриближение сильной св€зи предполагает, что имеетс€ совокупность большого числа изолированных атомов, у каждого из которых электроны имеют свою систему дискретных энергетических уровней. —в€зь электронов со своими атомами так сильна, что лишь валентные электроны при сближении атомов на рассто€ни€, сравнимые с размерами атомов, переход€т от одного атома к другому.
ѕриближение слабой св€зи полагает, что энерги€ взаимодействи€ электронов с решЄткой много меньше их кинетической энергии (например, в металлах). ¬ этом случае считают, что электроны в кристалле движутс€ внутри потенциальной €мы, размером с кристалл. Ёто позвол€ет пользоватьс€ уравнением ЎрЄдингера дл€ свободных электронов (модель электронного фермиЦгаза) внутри трЄхмерной потенциальной €мы кубической формы, учитыва€, однако, что электроны движутс€ в периодическом поле кристаллической решЄтки.
ак в модели сильной св€зи, так и в модели слабой св€зи (модели почти свободных электронов) на шкале энергии электронов имеютс€ участки разрешЄнных и запрещЄнных значений энергии, причЄм число электронных состо€ний в каждой разрешЄнной энергетической зоне кратно удвоенному числу атомов кристалла.
Ёнергетические зоны в кристаллах в приближении
—ильной св€зи
¬ изолированном атоме имеютс€ дискретные энергетические уровни энергии En,l. —читаетс€, что они завис€т от главного п и орбитального l квантовых чисел. ¬ то же врем€ энергетические уровни вырождены по квантовым числам т и тS, т.е. уровни, соответствующие различным значени€м магнитного и спинового квантовых чисел, совпадают.
Ёнергетические уровни электронов в атомах, наход€щихс€ в возбуждЄнных состо€ни€х, имеют конечную ширину ∆En,l, св€занную с соотношением неопределЄнности
∆En,l .τп 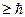
 ¬рем€ жизни атома в возбуждЄнном состо€нии
¬рем€ жизни атома в возбуждЄнном состо€нии  с, и тогда
с, и тогда  э¬. –ассто€ние между уровн€ми ~ 1 э¬.
э¬. –ассто€ние между уровн€ми ~ 1 э¬.
|
|
|
¬ газе соседние атомы ј и ¬ удалены друг от друга на рассто€ние L>>d (d Ц диаметр атома). ѕотенциальЦ ный барьер дл€ валентных электронов а и b в соседних атомах слишком широк, так, что веро€тность просачивани€ электронов сквозь него практически равна нулю. ѕоэтому все вещества в газообразном состо€нии ведут себ€ как диэлектрические среды до тех пор, пока внешние воздействи€ не вызовут их ионизацию.

¬ кристаллах рассто€ние между атомами столь мало (L~ d~ 10-10 м), что происходи перекрытие их электрических полей. ѕотенцииЦ альные кривые, разграничивающие соседние атомы, частично накладыЦ ваютс€ друг на друга и дают потенциальные кривые дл€ электронов типа а и b. ѕроисхоЦ дит понижение и сужение потенциЦ ального барьера дл€ валентных электронов атомов. «а счЄт туннельного эффекта электрон Ђуходитї от своего атома и переходит к соседнему.
ƒл€ упрощени€ вычислений можно считать, что потенциальный барьер пр€моугольный. “огда прозрачность барьера
 .
.
ƒл€ электрона в атоме толщина потенциального барьера d~ 10-10 м. “огда при  э¬ (10-18 ƒж) получаем D
э¬ (10-18 ƒж) получаем D  0,05.
0,05.
„исло ударов электрона о стенки барьера за единицу времени
 , где
, где
υ ~ 106 м/с Ц скорость движени€ электрона в атоме;
a ~ 10-10 м Ц ширина потенциальной Ђ€мыї, в которой находитс€
электрон.
¬рем€ жизни валентного электрона в атоме есть величина, обратна€ частоте:
 .
.
“.о. τ в этом случае на семь пор€дков меньше времени жизни валентного электрона в возбуждЄнном состо€нии изолированного атома. ѕри таких значени€х τ не имеет смысла говорить о принадлежности валентных электронов к определЄнным атомам. ќни станов€тс€ ЂобобществлЄннымиї и образуют квантовый электронный газ. Ёти электроны могут перемещатьс€ по всему кристаллу.
»з соотношени€ неопределЄнностей получаем оценку ширины энергетического уровн€ валентного электрона в кристалле
 2 э¬.
2 э¬.
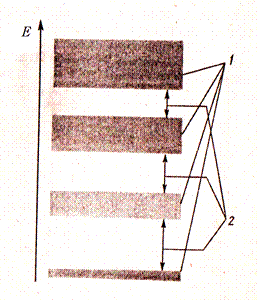 ”зкий энергетический уровень валентного электрона в изолированном атоме расшир€етс€ в кристалле в широкую полосу Ц зону разрешЄнных значений энергии электронов шириной пор€дка единиц электронЦвольт.
”зкий энергетический уровень валентного электрона в изолированном атоме расшир€етс€ в кристалле в широкую полосу Ц зону разрешЄнных значений энергии электронов шириной пор€дка единиц электронЦвольт.
–азрешЄнные энергетические зоны 1 отделены друг от друга зонами 2 запрещЄнных значений энергии электронов.
–азрешЄнна€ зона тем шире, чем больше энерги€ En,l электрона на соответствующем уровне в изолированном атоме.
¬озможные значени€ энергий электронов в пределах разрешЄнной энергетической зоны квантованы, а общее число их конечно.
¬ кристалле, состо€щем из N атомов, уровню энергии En,l изолированного атома соответствует зона, состо€ща€ из (2 l +1) N дискретных уровней, на каждом из которых может находитс€ не более двух электронов с антипараллельными спинами.
ƒл€ электронов внутренних оболочек атомов уменьшаетс€ прозрачность потенциального барьера и веро€тность туннельного перехода электрона от одного атома к другому оказываетс€ очень малой. Ќапример, дл€ электрона атома натри€ в основном состо€нии 1S среднее врем€ жизни  1020 лет. —ледовательно, электроны внутренних оболочек атомов в кристаллах прочно св€заны со Ђсвоимиї атомами и имеют энергетические уровни такие же узкие, как и в отдельном атоме.
1020 лет. —ледовательно, электроны внутренних оболочек атомов в кристаллах прочно св€заны со Ђсвоимиї атомами и имеют энергетические уровни такие же узкие, как и в отдельном атоме.
«онна€ структура в металлах, полупроводниках
» диэлектриках
—уществование энергетических зон позвол€ет объ€снить с единой точки зрени€ существование металлов, полупроводников и диэлектриков.
|
|
|
–азрешЄнную зону, полностью заполненную электронами и возникшую из того уровн€, на котором наход€тс€ валентные электроны в основном состо€нии атома, называют валентной зоной.
«она, заполненна€ электронами частично или пуста€ (при “ = 0 ), называетс€ зоной проводимости.
 ћеталлы.
ћеталлы.
а) ≈сли сама€ верхн€€ зона, содержаща€ электроны, заполнеЦ на лишь частично, то энергии теплового движени€ электронов (kT ~ 10-4 э¬) достаточно, чтобы электроны перешли на свободные уровни в этой зоне (стали свободными), обеспечива€ проЦ водимость металлов.
б) ≈сли валентна€ зона перекрываетс€ свободной зоной, то образуетс€ гибридна€ зона, котора€ заполнена валентными электронами лишь частично, что также обеспечивает проводимость металлического типа (например, у щелочноЦземельных металлов).
 ѕолупроводники.
ѕолупроводники.
≈сли уровни валентной зоны полностью зан€ты электронами, то дл€ того чтобы электрон попал в зону проводимости ему необходимо сообщить энергию, не меньшую, чем ширина запрещЄнной зоны ∆≈.
≈сли ∆≈ невелика (пор€дка нескольких дес€тых долей э¬) то энерги€ теплового движени€ оказываетс€ достаточной дл€ того, чтобы перевести часть электронов в верхнюю свободную зону проводимости. Ёти электроны будут находитьс€ в услови€х, аналогичных тем, в которых наход€тс€ валентные электроны в металле. ќдновременно станет возможным переход электронов валентной зоны на еЄ освободившиес€ верхние уровни. “акие вещества называютс€ собственными полупроводниками.
ƒиэлектрики.
≈сли ширина запрещЄнной зоны ∆≈ велика (условно более 2 э¬) то в этом случае кристалл называетс€ диэлетриком.
¬ твЄрдых диэлектриках электроны могут перемещатьс€ по кристаллу с тепловыми скорост€ми. ќднако это движение хаотично и не создаЄт направленного электронного Ђдрейфаї электрического тока. “епловое движение в этом случае не может забросить в свободную зону заметное число электронов.
—овременное представление о строении диэлектриков совершенно отличаетс€ от представлений о св€занных зар€дах, лежащих в основе классической теории диэлектриков.
Ёлектроны в кристаллах диэлектриков следует считать в некотором смысле более свободными, чем в металлах так как внешнее электрическое поле не может заставить их двигатьс€ в определЄнном направлении и создать электрический ток.
Ћекци€ 18






