ƒл€ перев≥рки теоретичноњ ≥ практичноњ п≥дготовки вступник≥в екзамен проводитьс€ у форм≥ тесту, складеного в≥дпов≥дно до ц≥Їњ програми. Ќа виконанн€ тесту в≥дведено 180 хвилин (3 години).
“ест складаЇтьс€ з двох частин:
1. „астина ј складаЇтьс€ з 70 тестових питань. ÷е завданн€ з вибором одн≥Їњ правильноњ в≥дпов≥д≥. «авданн€ формулюЇтьс€ у форм≥ питанн€ (задач≥) з к≥лькома (4-7) вар≥антами в≥дпов≥дей на нього (закрита форма тестового завданн€). —еред в≥дпов≥дей правильною Ї лише одна. ¬иконуючи завданн€, необх≥дно вказати правильний вар≥ант в≥дпов≥д≥.
2. „астина Ѕ включаЇ 3 практичних завданн€ (задач≥). ¬иконуючи завданн€, необх≥дно в≥дтворити ≥ записати повний х≥д розвТ€занн€.
IV. –»“≈–≤ѓ ќ÷≤Ќё¬јЌЌя
1. ѕравильна в≥дпов≥дь на питанн€ частини ј оц≥нюЇтьс€ в 1 бал, а неправильна Ц 0 бал≥в [ всього максимум за частину ј Ц 70 бал≥в ].
2. –озвТ€занн€ практичних завдань частини Ѕ оц≥нюЇтьс€ за диференц≥йованою шкалою [ всього максимум за частину Ѕ Ц 30 бал≥в ]: за кожну ≥з трьох задач частини Ѕ в≥д 0 до 10 бал≥в. «адач≥ вибираютьс€ випадково Ц одна ≥з номер≥в 1-10, друга ≥з номер≥в 11-20, трет€ ≥з номер≥в 21-30.
3. –озпод≥л бал≥в:
a. 0 бал≥в Ц завданн€ не розвТ€зане;
b. 2 бали - приведен≥ де€к≥ правильн≥ формули, €к≥ мають в≥дношенн€ до задач≥;
c. 4 бали Ц запропонована правильна ≥де€ розвТ€занн€, але допущен≥ помилки призвели до значного спотворенн€ в≥дпов≥д≥ (висновк≥в);
d. 6 бали Ц запропонована правильна ≥де€ розвТ€занн€, але допущен≥ помилки призвели до незначного спотворенн€ в≥дпов≥д≥ (висновк≥в); або не подано (подано на недостатньому р≥вн≥) обірунтуванн€ вибору способу розвТ€занн€;
e. 8 бал≥в Ц завданн€ розвТ€зане, подано обірунтуванн€ способу розвТ€занн€, але допущен≥ помилки техн≥чного характеру;
f. 10 бал≥в Ц завданн€ розвТ€зане повн≥стю (з обірунтуванн€м способу розвТ€занн€).
«агальна максимальна сума бал≥в: 100 бал≥в.
як працювати над тестом
Ќав≥ть €кщо ви впевненн≥ у правильност≥ в≥дпов≥д≥, уважно прочитайте вс≥ вар≥анти, щоб остаточно переконатис€ у правильност≥ свого вибору, €кщо вам здаютьс€ правильними два вар≥анти в≥дпов≥д≥, то вибирайте найб≥льш повний. ƒл€ в≥дпов≥д≥ на де€к≥ питанн€ потр≥бно буде виконати математичн≥ перетворенн€ (дл€ чернетки використовуйте пол€)
Ќеобх≥дно ретельно та охайно заповнити бланк в≥дпов≥дей дл€ частини ј, виданий разом ≥з тестовими завданн€ми.
| ’ |
ѕравильну в≥дпов≥дь необх≥дно позначити у бланку
–озвТ€зок задач частини Ѕ записуЇте безпосередньо п≥д умовами.
„астина ј.
- ристали можуть мати ос≥ поворотноњ симетр≥њ наступних пор€дк≥в
| ј) 1,2,3,4,5,6 | ¬) 1,2,3,4,6 |
| Ѕ) 2,3,4,5,6 | √) 2,3,4,6,7 |
- –еш≥ток Ѕраве ≥снуЇ
| ј) 7 | ¬) 15 |
| Ѕ) 14 | √) 230 |
- Ќа один вузол ќ÷ - гратки з пер≥одом гратки а припадаЇ обТЇм
ј) 
| ¬)  /4 /4
|
Ѕ)  /2 /2
| √)  /6 /6
|
- Ќа один вузол √÷ - гратки з пер≥одом гратки а припадаЇ обТЇм
ј) 
| ¬)  /4 /4
|
Ѕ)  /2 /2
| √)  /6 /6
|
- Ќайб≥льшу м≥жплощинну в≥дстань у прост≥й куб≥чн≥й гратц≥ мають площини с≥мейства
| ј) (1 0 0) | ¬) (1 1 1) |
| Ѕ) (1 1 0) | √) (3 1 1) |
- Ќайб≥льшу м≥жплощинну в≥дстань у ќ÷ - гратц≥ мають площини с≥мейства
| ј) (1 0 0) | ¬) (1 1 1) |
| Ѕ) (1 1 0) | √) (3 1 1) |
- Ќайб≥льшу м≥жплощинну в≥дстань у √÷ - гратц≥ мають площини с≥мейства
| ј) (1 0 0) | ¬) (1 1 1) |
| Ѕ) (1 1 0) | √) (3 1 1) |
- ≥льк≥сть найближчих сус≥д≥в у вузла простоњ куб≥чноњ гратки р≥вна
| ј) 6 | ¬) 12 |
| Ѕ) 8 | √) 4 |
- ≥льк≥сть найближчих сус≥д≥в у вузла ќ÷ - гратки р≥вна
| ј) 6 | ¬) 12 |
| Ѕ) 8 | √) 4 |
- ≥льк≥сть найближчих сус≥д≥в у вузла √÷ - гратки р≥вна
| ј) 6 | ¬) 12 |
| Ѕ) 8 | √) 4 |
- ≥льк≥сть найближчих сус≥д≥в у вузла гексагональноњ щ≥льнопакованоњ гратки
р≥вна
|
|
|
| ј) 6 | ¬) 12 |
| Ѕ) 8 | √) 4 |
- ≥льк≥сть найближчих сус≥д≥в у вузла алмазноњ гратки р≥вна
| ј) 6 | ¬) 12 |
| Ѕ) 8 | √) 4 |
- ѕараметр гратки, оберненоњ до простоњ куб≥чноњ з параметром а, р≥вний
ј) 
| ¬) 
|
Ѕ) 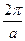
| √) 
|
- ѕараметр гратки, оберненоњ до ќ÷ -гратки, р≥вний
ј) 
| ¬) 
|
Ѕ) 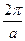
| √) 
|
- ѕараметр гратки, оберненоњ до √÷ -гратки, р≥вний
ј) 
| ¬) 
|
Ѕ) 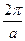
| √) 
|
- «вТ€зок м≥ж параметром гратки, м≥жплощинною в≥дстанню ≥ ≥ндексами ћ≥ллера
ј) 
| ¬) 
|
Ѕ) 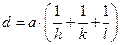
| √) 
|
- ѕроста куб≥чна гратка маЇ параметр гратки а. як≥ довжини хвил≥ можуть дати дифракц≥йну картину в≥д такоњ гратки?
ј) 
| ¬) 
|
Ѕ) 
| √) 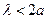
|
- ќ÷ - гратка маЇ параметр гратки а. як≥ довжини хвил≥ можуть дати дифракц≥йну картину в≥д такоњ гратки?
ј) 
| ¬) 
|
Ѕ) 
| √) 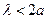
|
- √÷ - гратка маЇ параметр гратки а. як≥ довжини хвил≥ можуть дати дифракц≥йну картину в≥д такоњ гратки?
ј) 
| ¬) 
|
Ѕ) 
| √) 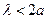
|
- Ѕазисн≥ вектори √÷ гратки:
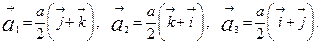 Ѕазисний вектор
Ѕазисний вектор  оберненоњ гратки
оберненоњ гратки
ј) 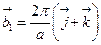
| ¬) 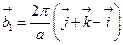
|
Ѕ) 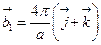
| √) 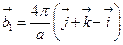
|
- Ѕазисн≥ вектори ќ÷ гратки:
 Ѕазисний вектор
Ѕазисний вектор  оберненоњ гратки
оберненоњ гратки
ј) 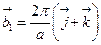
| ¬) 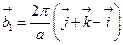
|
Ѕ) 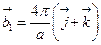
| √) 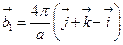
|
- ≤мов≥рн≥сть електрону рухатись без з≥ткнень прот€гом часу t р≥вна
ј) 
| ¬) 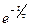
|
Ѕ) 
| √) 
|

|
- —ередн≥й квадрат часу до з≥ткненн€
ј) 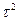
| ¬) 
|
Ѕ) 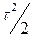
| √) 
|
- —ередн≥й куб часу до з≥ткненн€
ј) 
| ¬) 
|
Ѕ) 
| √) 
|
- ѕитомий оп≥р пров≥дника
ј) 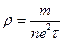
| ¬) 
|
Ѕ) 
| √) 
|
- ≈лектричне поле в метал≥ включили в момент t=0. √устина струму зм≥нюЇтьс€ з часом за законом:
ј) 
| ¬) 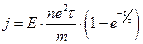
|
Ѕ) 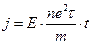
| √) 
|
- ‘ормула дл€ ефекту ’олла:
ј) 
| ¬) 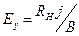
|
Ѕ) 
| √) 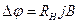
|
- «акон ¬≥демана-‘ранца дл€ теплопров≥дност≥
ј) 
| ¬) 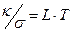
|
Ѕ) 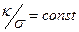
| √) 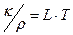
|
ј) 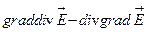
| ¬) 
|
Ѕ) 
| √) 
|
- Ќа кожну ком≥рку оберненого простору обТЇмом
 припадаЇ два квантових стани в≥льних електрон≥в ≥з протилежними сп≥нами. «найти зв≥дси енерг≥ю ‘ерм≥.
припадаЇ два квантових стани в≥льних електрон≥в ≥з протилежними сп≥нами. «найти зв≥дси енерг≥ю ‘ерм≥.
ј) 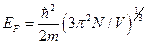
| ¬) 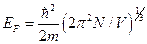
|
Ѕ) 
| √) 
|
- —ередн€ енерг≥€ в≥льних електрон≥в при
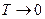
ј) 
| ¬) 
|
Ѕ) 
| √) 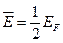
|
- “емпература ‘ерм≥ метал≥в маЇ пор€док
ј) 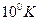
| ¬) 
|
Ѕ) 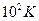
| √) 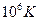
|
- ƒовжина хвил≥ де Ѕройл€ (за пор€дком величини), що в≥дпов≥даЇ енерг≥њ ‘ерм≥
ј) 
| ¬) 
|
Ѕ) 
| √) 
|
- –озпод≥л ‘ерм≥-ƒ≥рака
ј) 
| ¬) 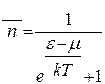
|
Ѕ) 
| √) 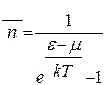
|
- ћол€рна теплоЇмн≥сть електронного газу
ј) 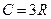
| ¬) 
|
Ѕ) 
| √) 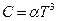
|
- —ередн€ енерг≥€ квантового гармон≥чного осцил€тора частотою

ј) 
| ¬) 
|
Ѕ) 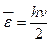
| √) 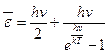
|
- ƒозволен≥ значенн€ енерг≥њ квантового гармон≥чного осцил€тора частотою
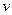
ј) 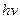
| ¬) 
|
Ѕ) 
| √) 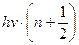
|
- «акон дисперс≥њ
 дл€ одноатомного ланцюжка з константою пружност≥
дл€ одноатомного ланцюжка з константою пружност≥ 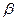 :
:
ј) 
| ¬) 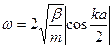
|
Ѕ) 
| √) 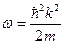
|
- “еплоЇмн≥сть д≥електрика при низьких температурах
ј) 
| ¬) 
|
Ѕ) 
|
√) 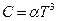 ƒ)
ƒ) 
|
- “еплоЇмн≥сть двовим≥рного д≥електрика при низьких температурах
ј) 
| ¬) 
|
Ѕ) 
| √) 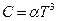 ƒ)
ƒ) 
|
- ѕотенц≥ал Ћенарда-ƒжонса
ј) 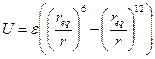
| ¬) 
|
Ѕ)  (де
(де  - р≥вноважна в≥дстань) - р≥вноважна в≥дстань)
| √) 
|
- ѕерша поправка до енерг≥њ в стац≥онарн≥й теор≥њ збурень (невироджений випадок)
ј) 
| ¬) 
|
Ѕ) 
| √) 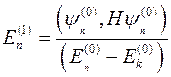
|
- —п≥вв≥дношенн€ Ѕора-√ейзенберга
ј) 
| ¬) 
|
Ѕ) 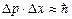
| √) 
|
- ѕроникн≥сть барТЇру висотою
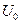 ≥ товщиною
≥ товщиною  дл€ частинки масою
дл€ частинки масою  ≥ енерг≥Їю ≈
≥ енерг≥Їю ≈
ј) 
| ¬) 
|
Ѕ) 
| √) 
|
|
|
|
- ѕров≥дн≥сть власних нап≥впров≥дник≥в з шириною забороненоњ зони
 залежить в≥д температури €к
залежить в≥д температури €к
ј) 
| ¬) 
|
Ѕ) 
| √) 
|
- який ≥з 4-х матер≥ал≥в не Ї нап≥впров≥дником
| ј)Si | ¬)GaAs |
| Ѕ)Ge | √)Bi |
- який ≥з перел≥чених матер≥ал≥в не стаЇ надпров≥дником при пониженн≥ температури.
| ј)Al | ¬)Ni |
| Ѕ)Nb | √)Pb |
- „им визначаЇтьс€ частота струму в нестац≥онарному ефект≥ ƒжозефсона
ј) 
| ¬) 
|
Ѕ) 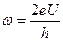
| √) 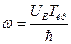
|
- ѕор€док величини енерг≥њ звТ€зку купер≥вськоњ пари в алюм≥н≥њ
| ј)10-19ƒж | ¬) 10-31ƒж |
| Ѕ) 10-23ƒж | √) 10-16ƒж |
- вант магн≥тного потоку
| ј) h/e | ¬) h/(2e) |
| Ѕ) 2h/e | √) 2e/h |
- ≤зотопний ефект критичноњ температури надпров≥дника
ј) 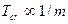
| ¬) 
|
Ѕ) 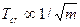
| √) 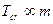
|
- „ому теплопров≥дн≥сть надпров≥дник≥в знижуЇтьс€ ≥з зниженн€м температури?
| ј) фонони пов≥льно рухаютьс€ | ¬) зменшуЇтьс€ частка Днормальних електрон≥вФ здатних до розс≥юванн€ ≥ перенесенн€ енерг≥њ |
| Ѕ) неправда-теплопров≥дн≥сть росте ≥з зниженн€м “ | √) зг≥дно з законом ¬≥демана-‘ранца |
- ќдиниц≥ вим≥рюванн€ напруженост≥ магн≥тного пол€
| ј) тесла | ¬) ¬ольт/метр |
| Ѕ) ампер/метр | √) гаус |
- ќдиниц≥ вим≥рюванн€ намагн≥ченост≥
| ј) тесла | ¬) ¬ольт/метр |
| Ѕ) ампер/метр | √) гаус |
- ќдиниц≥ вим≥рюванн€ ≥ндукц≥њ магн≥тного пол€
| ј) тесла | ¬) ¬ольт/метр |
| Ѕ) ампер/метр | √) ерстед |
- ’арактерн≥ значенн€ магн≥тноњ сприйн€тливост≥ д≥амагнетик≥в
| ј) 10-6 | ¬) 10-2 |
| Ѕ) -10-6 | √) -10-2 |
- ¬ибрати правильне р≥вн€нн€:
ј) 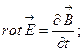
| ¬) 
|
Ѕ) 
| √) 
|
- «акон юр≥ дл€ парамагнетик≥в
ј) 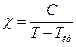
| ¬) 
|
Ѕ) 
| √) 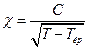
|
- «акон юр≥-¬ейса
ј) 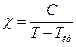
| ¬) 
|
Ѕ) 
| √) 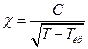
|
- Ќазвати антиферомагнетик
| ј)Fe | ¬)Ni |
| Ѕ)Cu | √)Cr |
- «вТ€зок м≥ж д≥амагн≥тною ≥ парамагн≥тною сприйн€тлив≥стю газу в≥льних електрон≥в
ј) 
| ¬) 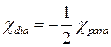
|
Ѕ) 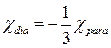
| √) 
|
- ¬становити узагальнен≥ ≥ндекси ћ≥ллера площин, що дають перш≥ 4 л≥н≥й дебаЇграми дл€ простоњ куб≥чноњ гратки
| ј)1 0 0 1 1 1 2 0 0 3 1 1 | ¬) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Ѕ)1 0 0 1 1 0 1 1 1 2 0 0 | √) 1 1 1 2 0 0 2 2 0 3 1 1 |
- ¬становити узагальнен≥ ≥ндекси ћ≥ллера площин, що дають перш≥ 4 л≥н≥й дебаЇграми дл€ ќ÷ -гратки
| ј)1 0 0 1 1 1 2 0 0 3 1 1 | ¬) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Ѕ) 1 0 0 1 1 0 1 1 1 2 0 0 | √) 1 1 1 2 0 0 2 2 0 3 1 1 |
- ¬становити узагальнен≥ ≥ндекси ћ≥ллера площин, що дають перш≥ 4 л≥н≥й дебаЇграми дл€ √÷ -гратки
| ј)1 0 0 1 1 1 2 0 0 3 1 1 | ¬) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Ѕ) 1 0 0 1 1 0 1 1 1 2 0 0 | √) 1 1 1 2 0 0 2 2 0 3 1 1 |
- «найти коеф≥ц≥Їнти упаковки (частка обТЇму, заповнена атомами-кул€ми) дл€ ѕ . ќкруглити до ц≥лих процент≥в.
| ј) 50 | ƒ) 74 |
| Ѕ) 52 | ≈) 82 |
| ¬) 62 | ∆) 100 |
| √) 68 |
- «найти коеф≥ц≥Їнти упаковки (частка обТЇму, заповнена атомами-кул€ми) дл€ ќ÷ . ќкруглити до ц≥лих процент≥в.
| ј) 50 | ƒ) 74 |
| Ѕ) 52 | ≈) 82 |
| ¬) 62 | ∆) 100 |
| √) 68 |
- «найти коеф≥ц≥Їнти упаковки (частка обТЇму, заповнена атомами-кул€ми) дл€ √÷ . ќкруглити до ц≥лих процент≥в.
| ј) 50 | ƒ) 74 |
| Ѕ) 52 | ≈) 82 |
| ¬) 62 | ∆) 100 |
| √) 68 |
- јлгоритм ћетропол≥са. «м≥на стану приймаЇтьс€, €кщо:
ј) 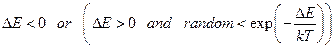
| ¬) 
|
Ѕ) 
| √) 
|
- јлгоритм √лаубера. «м≥на стану приймаЇтьс€, €кщо:
ј) 
| ¬) 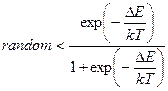
|
Ѕ) 
| √) 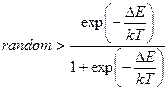
|
- јтом масою
 знаходитьс€ в потенц≥альному пол≥
знаходитьс€ в потенц≥альному пол≥  . «найти пер≥од його власних коливань.
. «найти пер≥од його власних коливань.
ј) 
| ¬) 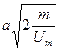
|
Ѕ) 
| √) 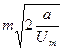
|
ƒ) 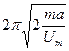
|
„астина Ѕ. «адач≥.
|
|
|
ѕ≥дчастина ≤
1. ¬ивести розпод≥л густини ≥мов≥рност≥ по часу до наступного з≥ткненн€ електрона у метал≥. «найти середн≥й час до наступного з≥ткненн€ електрона у метал≥. «найти середню енерг≥ю, що передаЇ електрон металу ≥онн≥й п≥дсистем≥ при з≥ткненн≥
2. «найти коеф≥ц≥Їнт теплопров≥дност≥ електронного газу в рамках класичноњ електронноњ теор≥њ. «найти число Ћоренца в закон≥ ¬≥демана-‘ранца.
3. «найти вираз дл€ диференц≥альноњ термо-е.р.с. дл€ металу в рамках класичноњ електронноњ теор≥њ.
4. –озвТ€зати к≥нетичне р≥вн€нн€ дл€ ≥мпульсу електрона у гармон≥йному електричному пол≥
5. «найти закон затуханн€ (зростанн€) струму при вимкненн≥ (ув≥мкненн≥) електричного пол€. «найти плазмову частоту €к частоту в≥льних коливань електронного газу
6. «найти ферм≥вський рад≥ус та енерг≥ю ‘ерм≥ у тривим≥рному та двовим≥рному кристалах
7. «найти вираз дл€ функц≥њ густини одноелектронних р≥вн≥в у метал≥ в рамках квантовоњ модел≥ в≥льних електрон≥в. «найти середнЇ значенн€ енерг≥њ в≥льних електрон≥в. «найти тиск газу в≥льних електрон≥в, €к≥ п≥дкор€ютьс€ статистиц≥ ‘ерм≥
8. «найти коеф≥ц≥Їнт упаковки дл€ ќ÷ , √÷ , ѕ ≥ √ўѕ граток
9. ƒовести, що в √÷ гратц≥ максимальна густина вузл≥в - у площинах {111}, а
в ќ÷ гратц≥ максимальна густина вузл≥в - у площинах {110}
10. ¬становити м≥ллер≥вськ≥ ≥ндекси площин, в≥дбиванн€ в≥д €ких даЇ перш≥ 5 л≥н≥й дебаЇграми дл€ ќ÷ гратки, дл€ √÷ гратки
ѕ≥дчастина ≤≤
11. «найти теплоЇмн≥сть твердого т≥ла в рамках модел≥ ≈йнштейна.
12. ƒовести (використовуючи модель ƒеба€), що теплоЇмн≥сть твердого т≥ла при низьких температурах пропорц≥йна кубу температури.
13. ƒовести (використовуючи модель ƒеба€), що теплоЇмн≥сть ƒ¬ќ¬»ћ≤–Ќќ√ќ твердого т≥ла при низьких температурах пропорц≥йна квадрату температури.
14. «найти вираз дл€ коеф≥ц≥Їнта теплового розширенн€, використовуючи модель ангармон≥йних коливань ≥з куб≥чним членом у енерг≥њ (U=beta/2*x^2-gamma/3*x^3)
15. «найти нормальн≥ моди коливань л≥н≥йноњ молекули ј-¬-ј (типу —ќ2) з масами атом≥в ћа, ћв ≥ жорстк≥стю пружних звТ€зк≥в к.
16. «найти закон дисперс≥њ пружних хвиль (залежн≥сть енерг≥њ в≥д хвильового вектора) у одноатомному ланцюжку. ¬≥дома маса атом≥в, середн€ в≥дстань м≥ж атомами ≥ жорстк≥сть пружного звТ€зку м≥ж сус≥дн≥ми атомами.
17. «найти закон дисперс≥њ поблизу границ≥ зони Ѕр≥ллюена в рамках одновим≥рноњ модел≥ слабкого звТ€зку при заданому слабкому пер≥одичному потенц≥ал≥ V(r).
18. ќписати модель сильного звТ€зку дл€ ќ÷ -гратки.
19. ¬ивести закон д≥ючих мас дл€ електрон≥в ≥ д≥рок у власному нап≥впров≥днику.
20. ¬ивести ≥ проанал≥зувати вираз дл€ оберненоњ ефективноњ маси електрона.
ѕ≥дчастина ≤≤≤.
21. ѕобудувати модель д≥амагнетика на основ≥ боровськоњ модел≥ атома. ќц≥нити д≥амагн≥тну сприйн€тлив≥сть твердого т≥ла.
22. ѕобудувати модель парамагнетика, вважаючи сп≥н кожного атома р≥вним одн≥й друг≥й, а проекц≥ю магн≥тного момента Ц плюс-м≥нус магнетону Ѕора.
23. ѕобудувати модель самоузгодженого пол€ ¬ейса. «вТ€зати параметр ¬ейса з точкою юр≥.
24. ѕобудувати модель ≤з≥нга в наближенн≥ самоузгодженого пол€. ¬иразити температуру фазового переходу спонтанного намагн≥чуванн€ через енерг≥ю обм≥нноњ взаЇмод≥њ.
25. «найти вираз дл€ обм≥нноњ взаЇмод≥њ дл€ випадку двоелектронноњ системи у вигл€д≥ ≥нтеграл≥в.
26. ќписати €к м≥н≥мум 10 властивостей надпров≥дник≥в.
27. «найти глибину проникненн€ магн≥тного пол€ в надпров≥дник у рамках теор≥њ Ћондон≥в.
28. «найти вираз критичноњ швидкост≥ дл€ надтекучого гел≥ю через закон дисперс≥њ елементарних збуджень у гел≥њ.
29. ƒовести властив≥сть квантуванн€ магн≥тного потоку пол€ надпров≥дника ≥з струмом на основ≥ теор≥њ √≥нзбурга-Ћандау.
|
|
|
30. ќписати нестац≥онарний ефект ƒжозефсона на основ≥ теор≥њ √≥нзбурга-Ћандау.
V. –≈ ќћ≈Ќƒќ¬јЌј Ћ≤“≈–ј“”–ј
ќсновна л≥тература.
1. „. иттель. ¬ведение в физику твердого тела. ћ.1978.
2. ј.јшкрофт, .ћермин. ‘изика твердого тела.“. 1,2. ћ.1979.
3. ƒж.«айман. ѕринципы теории твердого тела. ћ. 1974
4. ј.√усак, ¬.√риценко, “.«апорожець. —татистична ф≥зика - основн≥ положенн€ та модел≥. „еркаси. 1998.
5. ».»родов. «адачи по квантовой физике. ћ.1977.
ƒодаткова л≥тература.
6. .Ѕиндер, ƒ. ’еерман. ћоделирование методом ћонте- арло в статистической физике. ћ.1995.
7.ƒ. ’еерман. ћетоды компьютерного эксперимента в теоретической физике. ћ.1990.
8.„. иттель. вантова€ теори€ твердых тел. ћ.1967.
9. „. иттель. —татистическа€ термодинамика. ћ.1977.
10.ј. ћарадудин, «.ћонтролл, ƒж.¬ейсс, ƒинамика кристаллической решетки в гармоническом приближении. ћ.1965.
11. √усак ј.ћ., Ѕогатирьов ј.ќ., «апорожец “.¬. и др. (ѕод ред. √усака ј.ћ.) ћодели твердофазных реакций. »зд. „еркасского университета, 2004.
12. Gusak A. Diffusion, Reactions, Coarsening Ц some new ideas. Cherkasy National University Publ., Cherkasy Ц monograph (in English), 2004
13. Gusak, A.M., and F. Hodaj. УNucleation in a Concentration Gradient.Ф Chapter 10 in У Nucleation Theory and ApplicationsФ, ed.J.Schmelzer, Wiley VCH (2005): 375-417.
14. ј.ћ.√усак. “ермодинамика необратимых процессов Ц глава в энциклопедии ДЌеорганическое материаловедениеФ, под ред. √.√.√несина и ¬.¬.—корохода, »нститут проблем материаловедени€ ЌјЌ ”краины, с.с. 239-260 (2008)
√олова фаховоњ атестац≥йноњ ком≥с≥њ проф., д.ф.-м.н. ј.ћ.√усак







