Алгоритм розв’язку задачі (1) – (2) складається з двох етапів.
Етап I. Параметру  надають фіксоване значення, наприклад
надають фіксоване значення, наприклад
 .
.
Цим задача приводиться до задачі лінійного програмування.
Розв’язуючи отриману ЗЛП симплекс-методом, знаходять вершину, в якій  досягає максимум.
досягає максимум.
Етап II. Визначають інтервал зміни параметра  , для якого максимум
, для якого максимум  , досягається в одній і тій же вершині многогранника
, досягається в одній і тій же вершині многогранника  .
.
Знайдений інтервал виключається із відрізка  для частини відрізка, що залишилася, знову розв’язують ЗЛП симплекс-методом тобто переходимо до етапу I.
для частини відрізка, що залишилася, знову розв’язують ЗЛП симплекс-методом тобто переходимо до етапу I.
Розв’язок продовжується до тих пір поки весь відрізок  не буде розбито на частинні інтервали.
не буде розбито на частинні інтервали.
Задача. Знайти інтервали зміни параметра t на відрізку  , для яких
, для яких

досягає максимум в одній і тій же вершині області допустимих значень системи обмежень.


Розв’язання.
Етап I.
1. Покладемо
 .
.
Тоді функція  прийме вигляд
прийме вигляд
 . (7)
. (7)
Всі дані задачі заносимо в жорданову таблицю.
В рядок  цієї таблиці в кожен стовпчик записуємо число, яке рівне сумі чисел
цієї таблиці в кожен стовпчик записуємо число, яке рівне сумі чисел  і
і  .
.
Крім того, додамо до таблиці два рядки для запису функції  з довільним параметром
з довільним параметром  (табл. 1).
(табл. 1).
При цьому в передостанньому рядку записуємо коефіцієнти  , а в останньому –
, а в останньому –  .
.
Щоб отримати  , потрібно перемножити коефіцієнти останнього рядка на
, потрібно перемножити коефіцієнти останнього рядка на  і додати їх до коефіцієнтів передостаннього.
і додати їх до коефіцієнтів передостаннього.
Таблиця 1

| … | 
| ||
 = =
| 
| 
| ||
| … | … | |||
 = =
| 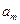
| |||

| 
| … | 
| |

| 
| … | 
| |

| … | 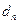
|
2. Знаходимо оптимальний план задачі звичайним симплекс-методом, здійснюючи перетворення і елементів останніх двох рядків.
Припустимо, що план, представлений в таблиці 2, є оптимальним.
Таблиця 2
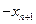
| 
| 
| 
| 
| 
| ||

| 
| ||||||

| 
| ||||||

| 
| ||||||

| 
| 
| |||||

| 
| ||||||

| 
| 
| 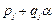
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
|
Тоді всі коефіцієнти рядка  – невід’ємні:
– невід’ємні:
 .
.
Оскільки оптимальний план знайдено, переходимо до виконання дій другого етапу.
Етап II.
1. Знаходимо значення параметра  , при яких план в табл. 2 буде залишатись оптимальним (максимум
, при яких план в табл. 2 буде залишатись оптимальним (максимум  досягається в тій самій вершині).
досягається в тій самій вершині).
Для цього необхідно, щоб всі коефіцієнти функції  були невід’ємні:
були невід’ємні:
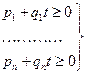 (8)
(8)
Із системи (8) видно, що у всіх випадках, крім  (при
(при  нерівність
нерівність  виконується при будь-яких значеннях
виконується при будь-яких значеннях  ; відповідно, на стовпчик, в якому знаходиться
; відповідно, на стовпчик, в якому знаходиться  , можна не звертати уваги), границею зміни параметра
, можна не звертати уваги), границею зміни параметра  служить відношення
служить відношення
 .
.
Тому передивляємось останні елементи  останнього рядка таблиці:
останнього рядка таблиці:
· якщо всі вони більші нуля, переходимо до пункту 2;
· якщо всі вони менші нуля – до пункту 3;
· якщо ж серед елементів  є і додатні, і від’ємні – до пункту 4.
є і додатні, і від’ємні – до пункту 4.
2. Нехай всі 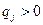 .
.
Серед відношень

вибираємо найбільше.
Верхньої межі для  в цьому випадку не існує.
в цьому випадку не існує.
Таким чином,
 (9)
(9)
В інтервалі  функція
функція  досягає максимум в тій самій вершині, що й при
досягає максимум в тій самій вершині, що й при  ; відповідно,
; відповідно,  .
.
3. Нехай всі  .
.
Серед відношень

вибираємо найменше.
Якщо взяти
 ,
,
то всі умови (8) будуть задоволені.
Нижньої межі для  в цьому випадку не існує, тому його можна зменшувати нескінченно.
в цьому випадку не існує, тому його можна зменшувати нескінченно.
Отже,
 (10)
(10)
Як і раніше,  .
.
4. Нехай серед елементів  є як додатні, так і від’ємні.
є як додатні, так і від’ємні.
Розділимо систему нерівностей (8) на дві підсистеми відповідно до знаків коефіцієнтів  .
.
Тоді із підсистеми нерівностей з
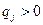
отримаємо
 ,
,
а з другої підсистеми з

будемо мати
 .
.
Відповідно, вся система нерівностей (8) буде задовольнятись, якщо  буде приймати значення:
буде приймати значення:
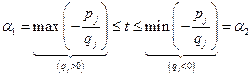 (11)
(11)
В цьому випадку виділений інтервал, в якому функція досягає максимум в тій самій вершині, що й при  , є відрізком
, є відрізком
 .
.
5. Зрівняємо отриманий інтервал  з заданим
з заданим  .
.
Незалежно від значення  лівою границею першого інтервалу буде
лівою границею першого інтервалу буде  , так як
, так як  більше
більше  бути не може.
бути не може.
Якщо
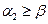 ,
,
то весь інтервал  попадає всередину інтервалу
попадає всередину інтервалу  , і задача розв’язана.
, і задача розв’язана.
Для будь-якого значення параметра 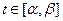 максимум функції
максимум функції  досягається в одній і тій самій вершині (рис. 4).
досягається в одній і тій самій вершині (рис. 4).

Рис. 4 Рис. 5
6.Якщо  , то в інтервалі
, то в інтервалі  максимум функції
максимум функції  буде в знайденій вершині (рис. 5).
буде в знайденій вершині (рис. 5).
Виключаємо цей інтервал із розгляду і розв’язуємо задачу для інтервалу, що залишився  .
.
Для цього  надаємо значення
надаємо значення  і замінюємо рядок
і замінюємо рядок  рядком
рядком  .
.
В результаті заміни отримаємо нову таблицю (табл. 3).
Таблиця 3
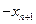
| 
| 
| 
| 
| 
| ||

| 
| ||||||

| 
| ||||||

| 
| ||||||

| 
| 
| |||||
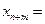
| 
| ||||||

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 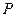
|

| 
| 
| 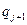
| 
| 
| 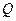
|
За розв’язуючий стовпчик в новій таблиці вибирається той, по якому визначено значення  (в цьому стовпчику на перетині з
(в цьому стовпчику на перетині з  – рядком знаходиться елемент, рівний нулю).
– рядком знаходиться елемент, рівний нулю).
Якщо нулі знаходяться в кількох стовпцях, то за розв’язуючий можна брати будь-який з них.
Розв’язуючий елемент знаходимо по найменшому симплексному відношенню і робимо один крок модифікованих жорданових виключень.
Отримаємо наступний по порядку оптимальний розв’язок, так як всі коефіцієнти в стрічці  при перетворенні не зміняться.
при перетворенні не зміняться.
Для знайденого розв’язку знову визначаємо інтервал зміни параметра  , для чого переходимо до пункту 1.
, для чого переходимо до пункту 1.
Якщо в розв’язуючому стовпчику не виявиться невід’ємних коефіцієнтів, то функція  при
при 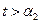 необмежена; задача на інтервалі
необмежена; задача на інтервалі  , що залишився розв’язку не має.
, що залишився розв’язку не має.
Зауваження. При відшуканні оптимального розв’язку для  (при виконанні пункту 2 етапу І алгоритму) може виявитися, що функція
(при виконанні пункту 2 етапу І алгоритму) може виявитися, що функція  зверху необмежена.
зверху необмежена.
В цьому випадку в розв’язуючому стовпчику  коефіцієнт
коефіцієнт  - стрічки від’ємний
- стрічки від’ємний  , а всі інші коефіцієнти стовпчика
, а всі інші коефіцієнти стовпчика  недодатні.
недодатні.
При значенні  на перетині стрічки
на перетині стрічки  і стовпчика
і стовпчика  буде елемент
буде елемент
 .
.
Нас цікавить значення цього елемента, так як вони визначають поведінку функції при
 .
.
Виберемо таке значення  , при якому коефіцієнт
, при якому коефіцієнт
 .
.
Звідси отримуємо, що
 .
.
Якщо значення елемента  , то для всіх
, то для всіх  коефіцієнт розв’язуючого стовпчика в стрічці
коефіцієнт розв’язуючого стовпчика в стрічці  буде від’ємним
буде від’ємним
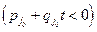 .
.
Отже, на всьому заданому відрізку  цільова функція
цільова функція  необмежена (задача розв’язку не має).
необмежена (задача розв’язку не має).
Якщо елемент  , то при
, то при  коефіцієнт, що знаходиться в розв’язуючому стовпчику та
коефіцієнт, що знаходиться в розв’язуючому стовпчику та  -стрічці, буде від’ємним.
-стрічці, буде від’ємним.
Значить і в цьому випадку цільова функція необмежена і задача розв’язку не має.
При значенні  коефіцієнт
коефіцієнт
 ,
,
а при подальшому збільшенні  він буде додатнім.
він буде додатнім.
До відрізку  застосовуємо послідовно весь алгоритм розв’язку задачі.
застосовуємо послідовно весь алгоритм розв’язку задачі.
Приклад 3. Знайти розв’язок задачі з прикладу 1 при зміні параметра  на відрізку [0,12].
на відрізку [0,12].
Розв’язок. Припускаємо  .
.
Тоді
 .
.
Заносимо умову задачі в таблицю 4 і розв’язуємо її симплекс-методом.
Опускаючи подробиці, наводимо оптимальний розв’язок (табл. 5.):
 .
.
Визначаємо значення параметра 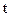 , при яких оптимальний розв’язок в тій самій вершині, що й при
, при яких оптимальний розв’язок в тій самій вершині, що й при  .
.
Так як в останньому рядку елемент
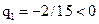 , а
, а  ,
,
то для визначення значень 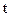 , при яких максимум буде досягатись в знайденій вершині, підставимо відповідні значення в відношення (11), отримаємо
, при яких максимум буде досягатись в знайденій вершині, підставимо відповідні значення в відношення (11), отримаємо

Таблиця 4. Таблиця 5

| 
| 
| 
| |||||

| -5 | 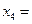
| 14/3 | 1/30 | 7/30 | |||
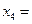
| -5 | -1 | -1 | 
| 25/3 | 1/6 | 1/6 | |

| -1 | 
| 3/10 | 1/10 | ||||

| 
| 4/3 | -2/15 | 1/15 | ||||

| -4 | -2 | 
| 2/5 | 4/5 | |||

| -4 | -2 | 
| 2/5 | 4/5 | |||
| -1 | 4/3 | -2/15 | 1/15 |
Тут  , а
, а  .
.
Отриманий інтервал менший заданого  , тому його виключаємо з подальшого розгляду і розв’язуємо задачу для інтервалу, що залишився
, тому його виключаємо з подальшого розгляду і розв’язуємо задачу для інтервалу, що залишився  .
.
Для цього даємо  значення
значення  і обчислюємо для нього рядок
і обчислюємо для нього рядок  .
.
Занесемо елементи  - рядка в табл. 6. Всі інші елементи таблиці залишаємо без змін.
- рядка в табл. 6. Всі інші елементи таблиці залишаємо без змін.
Таблиця 6 Таблиця 7

| 
| 
| 
| |||||
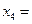
| 14/3 | 1/30 | 7/30 | 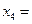
| 31/9 | |||

| 25/3 | 1/6 | 1/6 | 
| 20/9 | |||

| 3/10 | 1/10 | 
| 110/3 | ||||

| 4/3 | -2/15 | 1/15 | 
| 56/9 | |||

| 
| |||||||

| 2/5 | 4/5 | 
| 64/3 | -4/3 | 2/3 | ||
| 4/3 | -2/15 | 1/15 | 56/9 | 4/9 | 1/9 |
В першому стовпчику і  - рядку табл. 6. знаходиться нуль, тому цей стовпець беремо за розв’язуючий (при
- рядку табл. 6. знаходиться нуль, тому цей стовпець беремо за розв’язуючий (при 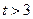 на місце нуля першим з’явиться від’ємне число і план перестане бути оптимальним).
на місце нуля першим з’явиться від’ємне число і план перестане бути оптимальним).
Знаходимо розв’язуючий елемент по найменшому симплексному відношенню і переходимо до нової таблиці (табл. 7).
План

в табл. 7 оптимальний, так як всі елементи  - рядка невід’ємні.
- рядка невід’ємні.
В останньому рядку всі елементи 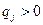 , відповідно, застосовуємо формулу (7) і визначаємо, що
, відповідно, застосовуємо формулу (7) і визначаємо, що
 ,
,
тобто  .
.
Так як значення  , то задача розв’язана.
, то задача розв’язана.
Отже, при

максимальне значення функції досягається у вершині  , при
, при

максимальне значення функції досягається у вершині  (рис. 3). При значенні
(рис. 3). При значенні  оптимум досягається у вершинах
оптимум досягається у вершинах 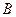 і
і  , а також в їх випуклій лінійній комбінації.
, а також в їх випуклій лінійній комбінації.






