–озгл€немо р≥шенн€ другоњ задач≥ динам≥ки в декартов≥й систем≥ координат. ќск≥льки в загальному випадку сила 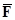 може залежати в≥д часу, в≥д координат точки та в≥д швидкост≥, то диференц≥альн≥ р≥вн€нн€ руху мають вигл€д:
може залежати в≥д часу, в≥д координат точки та в≥д швидкост≥, то диференц≥альн≥ р≥вн€нн€ руху мають вигл€д:
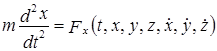

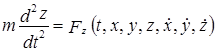
¬изначенн€ закону руху в цьому випадку зводитьс€ до ≥нтегруванн€ системи трьох диференц≥альних р≥вн€нь другого пор€дку, в €ких нев≥домими функц≥€ми с координати x, y, z точки, що рухаЇтьс€; а аргументом Ц час t.
ѕри ≥нтегруванн≥ кожного р≥вн€нн€ системи (2.13) з'€вл€ютьс€ дв≥ стал≥ ≥нтегруванн€, а дл€ випадку трьох основних диференц≥альних р≥вн€нь маЇмо ш≥сть сталих —1, —2, —3, —4, —5, —6.
ожна з координат x, y, z точки, що рухаЇтьс€, п≥сл€ ≥нтегруванн€ системи, залежить в≥д часу t та вс≥х шести пост≥йних ≥нтегруванн€:
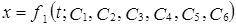 ;
;
 ;
;
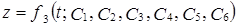 .
.
якщо сталим ≥нтегруванн€ надати р≥зн≥ числов≥ значенн€, то можна отримати сукупн≥сть р≥зних значень х, у, z.
“аким чином, надан≥ сили не визначають конкретного руху точки, а вид≥л€ють ц≥лий клас рух≥в, що характеризуютьс€ ш≥стьма дов≥льними сталими. ƒл€ того, щоб отримати р≥шенн€ конкретноњ задач≥, необх≥дно задати ще додатков≥ умови, що характеризують дану задачу. ¬ €кост≥ таких умов задають звичайно початков≥ умови руху.
¬ивченн€ будь-€кого руху починаЇтс€ з де€кого визначеного моменту часу, що називаЇтьс€ початковим моментом часу. ¬≥д цього моменту ми будемо в≥драховувати час руху, вважаючи, що в початковий момент t = 0. ѕочатковий стан точки будемо визначати њњ рад≥ус-вектором 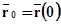 , та швидк≥стю
, та швидк≥стю 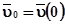 при t = 0.
при t = 0.
¬ декартових координатах необх≥дно задавати в≥дпов≥дн≥ проекц≥њ при t = 0:
x=x0 ; y=y0; z=z0;
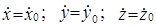 .
.
÷≥ в≥дношенн€ називаютьс€ початковими умовами руху.
« цих р≥вн€нь визначають стал≥ ≥нтегруванн€  в залежност≥ в≥д початкових координат точки та проекц≥й початковоњ швидкост≥. якщо п≥дставити отриман≥ значенн€ сталих ≥нтегруванн€, то отримаЇмо частинн≥ р≥шенн€ р≥вн€нь руху:
в залежност≥ в≥д початкових координат точки та проекц≥й початковоњ швидкост≥. якщо п≥дставити отриман≥ значенн€ сталих ≥нтегруванн€, то отримаЇмо частинн≥ р≥шенн€ р≥вн€нь руху:
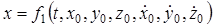 ,
,
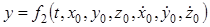 ,
,
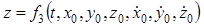 .
.
” випадку руху точки в площин≥, наприклад ’ќY, маЇмо два диференц≥альних р≥вн€нн€ руху. –≥шенн€ цих р≥вн€нь м≥стить вже чотири сталих ≥нтегруванн€, котр≥ визначаютьс€ з початкових умов: приt = 0,
x=x0 ; y=y0; 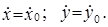
якщо точка виконуЇ пр€мол≥н≥йний рух, наприклад, в напр€мку ос≥ ќх, то маЇмо т≥льки одне диференц≥альне р≥вн€нн€, в р≥шенн€ €кого вход€ть т≥льки дв≥ стал≥ ≥нтегруванн€. ƒл€ њх визначенн€ необх≥дно задати так≥ початков≥ умови.
 ѕри t = 0; x=x0 ;.
ѕри t = 0; x=x0 ;.
Ќеобх≥дно зауважити, що введенн€ початковоњ швидкост≥ точки враховуЇ вплив на њњ рух тих сил, €к≥ д≥€ли на точку до початкового моменту часу.






