”„≈ЅЌќ≈ ѕќ—ќЅ»≈ ѕќ —ѕќ–“»¬Ќќ… ћ≈“–ќЋќ√»»
“ема 1. ќсновы теории измерений
“ема 2. »змерительные системы и их использование в физическом воспитании и спорте
“ема 3. “естирование общей физической подготовленности занимающихс€ физкультурой и спортом
“ема 4. ћатематическа€ статистика, ее основные пон€ти€ и приложение к физической культуре и спорту
“ема 5. ќпределение основных статистических показателей (ќ—ѕ) дл€ характеристики совокупностей
“ема 6. ќпределение доверительного интервала дл€ среднего значени€ генеральной совокупности по —тьюденту
“ема 7. —равнение групп методом —тьюдента
“ема 8. ‘ункциональна€ и коррел€ционна€ взаимосв€зи
“ема 9. –егрессионный анализ
“ема 10. ќпределение надежности тестов
“ема 11. ќпределение информативности и добротности теста
“ема 12. ќсновы теории оценок и норм
“ема 13. ќпределение норм в спорте
“ема 14. оличественна€ оценка качественных характеристик
“ема 15. онтроль за силовыми качествами
“ема 16. онтроль за уровнем развити€ гибкости и выносливости
“ема 17. онтроль за объемом и интенсивностью нагрузки
“ема 18. онтроль за эффективностью техники
“ема 19. ќсновы теории управл€емых систем
“ема 20. омплексна€ оценка физической подготовленности исследуемых
“≈ћј 1. ќ—Ќќ¬џ “≈ќ–»» »«ћ≈–≈Ќ»…
ѕ–≈ƒћ≈“ —ѕќ–“»¬Ќќ… ћ≈“–ќЋќ√»»
—лово "метрологи€" в переводе с древнегреческого означает "наука об измерени€х" (метрон Ч мера, логос Ч слово, наука).
ќсновной задачей общей метрологии €вл€етс€ обеспечение единства и точности измерений. —портивна€ метрологи€ как научна€ дисциплина представл€ет собой часть общей метрологии. ее основным задачам относ€тс€:
1. –азработка новых средств и методов измерений.
2. –егистраци€ изменений в состо€нии занимающихс€ под вли€нием различных физических нагрузок.
3. —бор массовых данных, формирование систем оценок и норм.
4. ќбработка полученных результатов измерений с целью организации эффективного контрол€ и управлени€ учебно-тренировочным процессом.
ќднако как учебна€ дисциплина спортивна€ метрологи€ выходит за рамки общей метрологии. “ак, в физическом воспитании и спорте помимо обеспечени€ измерени€ физических величин, таких как длина, масса и т.д., подлежат измерению педагогические, психологические, биологические и социальные показатели, которые по своему содержанию нельз€ назвать физическими. ћетодикой их измерений обща€ метрологи€ не занимаетс€ и, поэтому, были разработаны специальные измерени€, результаты которых всесторонне характеризуют подготовленность физкультурников и спортсменов.
»спользование методов математической статистики в спортивной метрологии дало возможность получить более точное представление об измер€емых объектах, сравнить их и оценить результаты измерений.
¬ практике физического воспитани€ и спорта провод€т измерени€ в процессе систематического контрол€ (фр. проверка чего-либо), в ходе которого регистрируютс€ различные показатели соревновательной и тренировочной де€тельности, а также состо€ние спортсменов. “акой контроль называют комплексным.
Ёто дает возможность установить причинно-следственные св€зи между нагрузками и результатами в соревновани€х. ј после сопоставлени€ и анализа разработать программу и план подготовки спортсменов.
“аким образом, предметом спортивной метрологии €вл€етс€ комплексный контроль в физическом воспитании и спорте и использование его результатов в планировании подготовки спортсменов и физкультурников.
—истематический контроль за спортсменами позвол€ет определить меру их стабильности и учитывать возможные погрешности измерений.
|
|
|
“ема: ќсновы теории измерений
÷ель: научитьс€ осуществл€ть корректную постановку задач измерени€,
выбирать единицы, средства и методы измерени€, определ€ть их точность.
“еоретические сведени€
»змерением (в широком смысле слова) называют установление соответстви€ между изучаемыми €влени€ми, с одной стороны, и числами, с другой.
„тобы результаты разных измерений можно было сравнивать друг с другом, они должны быть выражены в одних и тех же единицах. ¬ 1960 г. на ћеждународной генеральной конференции по мерам и весам была прин€та ћеждународна€ система единиц, получивша€ сокращенное название —».
—» в насто€щее врем€ включает семь независимых друг от друга основных единиц, из которых в качестве производных вывод€т единицы остальных физических величин. ѕроизводные единицы определ€ютс€ на основе формул, св€зывающих между собой физические величины.
Ќапример, единица длины (метр) и единица времени (секунда) Ч основные единицы, а единица скорости (метр за секунду [м/с]) Ч производна€. —овокупность выбранных основных и образованных с их помощью производных единиц дл€ одной или нескольких областей измерени€ называетс€ системой единиц (табл. 1).
“аблица 1
ќсновные единицы —»
| ≈диница |
| ¬еличина | –азмерность | Ќазвание | ќбозначение |
| русское | международное | |||
| ƒлина | L | ћетр | м | m |
| ћасса | M | илограмм | кг | kg |
| ¬рем€ | T | —екунда | с | S |
| —ила эл. тока | I | јмпер | ј | A |
| “емпература | q | ельвин | K | |
| ол-во вещ-ва | N | ћоль | моль | mol |
| —ила света | G | анделла | д | cd |
ƒл€ образовани€ кратных и дольных единиц должны использоватьс€ специальные приставки (табл. 2).
“аблица 2
ћножители и приставки
| ћножители | ѕриставка |
| 1 000 000=106 | ћега | ћ |
| 1 000=103 | ило | к |
| 100=102 | √екто | √ |
| 10=101 | ƒека | ƒ |
| 0,1=10-1 | деци | d |
| 0,01=10-2 | санти | с |
| 0,001=10-3 | милли | m |
| 0,000 001=10-6 | микро | m |
¬се производные величины имеют свои размерности.
–азмерностью называетс€ выражение, св€зывающее производную величину с основными величинами системы при коэффициенте пропорциональности, равном единице. Ќапример, размерность скорости равна 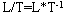 , а размерность ускорени€ равна
, а размерность ускорени€ равна 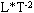
Ќикакое измерение не может быть выполнено абсолютно точно. –езультат измерени€ неизбежно содержит погрешность, величина которой тем меньше, чем точнее метод измерени€ и измерительный прибор.
ќсновна€ погрешность Ч это погрешность метода измерени€ или измерительного прибора, котора€ имеет место в нормальных услови€х их применени€.
ƒополнительна€ погрешность Ч это погрешность измерительного прибора, вызванна€ отклонением условий его работы от нормальных.
¬еличина D ј=ј-ј0, равна€ разности между показанием измерительного прибора (ј) и истинным значением измер€емой величины (ј0), называетс€ абсолютной погрешностью измерени€. ќна измер€етс€ в тех же единицах, что и сама измер€ема€ величина.
ќтносительна€ погрешность Ч это отношение абсолютной погрешности к значению измер€емой величины:

¬ тех случа€х, когда оцениваетс€ не погрешность измерени€, а погрешность измерительного прибора, за максимальное значение измер€емой величины принимают предельное значение шкалы прибора. ¬ таком понимании наибольшее допустимое значение D ѕа, выраженное в процентах, определ€ет в нормальных услови€х работы класс точности измерительного прибора.
—истематической называетс€ погрешность, величина которой не мен€етс€ от измерени€ к измерению. ¬ силу этой своей особенности систематическа€ погрешность часто может быть предсказана заранее или в крайнем случае обнаружена и устранена по окончании процесса измерени€.
“арированием (от нем. tarieren) называетс€ проверка показаний измерительных приборов путем сравнени€ с показани€ми образцовых значений мер (эталонов*) во всем диапазоне возможных значений измер€емой величины.
алибровкой называетс€ определение погрешностей или поправка дл€ совокупности мер (например, набора динамометров). » при тарировании, и при калибровке к входу измерительной системы вместо спортсмена подключаетс€ источник эталонного сигнала известной величины. Ќапример, тариру€ установку дл€ измерени€ усилий, на тензометрической платформе поочередно помещают грузы весом 10, 20, 30 и т.д. килограммов.
–андомизацией (от англ. random Ч случайный) называетс€ превращение систематической погрешности в случайную. Ётот прием направлен на устранение неизвестных систематических погрешностей. ѕо методу рандомизации измерение изучаемой величины производитс€ несколько раз. ѕри этом измерени€ организуют так, чтобы посто€нный фактор, вли€ющий на их результат, действовал в каждом случае по-разному. —кажем, при исследовании физической работоспособности можно рекомендовать измер€ть ее многократно, вс€кий раз мен€€ способ задани€ нагрузки. ѕо окончании всех измерений их результаты усредн€ютс€ по правилам математической статистики.
—лучайные погрешности возникают под действием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удаетс€.
—тандарт Ч нормативно-технический документ, устанавливающий комплекс норм, правил, требований к объекту стандартизации и утвержденный компетентным органом Ч √осударственным комитетом по стандартизации. ¬ спортивной метрологии объектом стандартизации €вл€ютс€ спортивные измерени€.
|
|
|
Ўкала наименований (номинальна€ шкала)
Ёто сама€ проста€ из всех шкал. ¬ ней числа выполн€ют роль €рлыков и служат дл€ обнаружени€ и различени€ изучаемых объектов (например, нумераци€ игроков футбольной команды). „исла, составл€ющие шкалу наименований, разрешаетс€ мен€ть местами. ¬ этой шкале нет отношений типа "больше Ч меньше", поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. ѕри использовании шкалы наименований могут проводитс€ только некоторые математические операции. Ќапример, ее числа нельз€ складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречаетс€ то или иное число.
Ўкала пор€дка
≈сть виды спорта, где результат спортсмена определ€етс€ только местом, зан€тым на соревновани€х (например, единоборства). ѕосле таких соревнований €сно, кто из спортсменов сильнее, а кто слабее. Ќо насколько сильнее или слабее, сказать нельз€. ≈сли три спортсмена зан€ли соответственно первое, второе и третье места, то каковы их различи€ в спортивном мастерстве, остаетс€ не€сным: второй спортсмен может быть почти равен первому, а может быть существенно слабее его и быть почти одинаковым с третьим. ћеста, занимаемые в шкале пор€дка, называютс€ рангами, а сама шкала называетс€ ранговой или неметрической. ¬ такой шкале составл€ющие ее числа упор€дочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельз€. ¬ отличие от шкалы наименований шкала пор€дка позвол€ет не только установить факт равенства или неравенства измер€емых объектов, но и определить характер неравенства в виде суждений: "больше Ч меньше", "лучше Ч хуже" и т.п.
— помощью шкал пор€дка можно измер€ть качественные, не имеющие строгой количественной меры, показатели. ќсобенно широко эти шкалы используютс€ в гуманитарных науках: педагогике, психологии, социологии. рангам шкалы пор€дка можно примен€ть большее число математических операций, чем к числам шкалы наименований.
|
|
|
Ўкала интервалов
Ёто така€ шкала, в которой числа не только упор€дочены по рангам, но и разделены определенными интервалами. ќсобенность, отличающа€ ее от описываемой дальше шкалы отношений, состоит в том, что нулева€ точка выбираетс€ произвольно. ѕримерами могут быть календарное врем€ (начало летоисчислени€ в разных календар€х устанавливалось по случайным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечь€ может приниматьс€ равным либо нулю, либо 180о), температура, потенциальна€ энерги€ подн€того груза, потенциал электрического пол€ и др.
–езультаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычислени€ отношений. ƒанные шкалы интервалов дают ответ на вопрос "на сколько больше?", но не позвол€ют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Ќапример, если температура повысилась с 10о до 20о по ÷ельсию, то нельз€ сказать, что стало в два раза теплее.
Ўкала отношений
Ёта шкала отличаетс€ от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Ѕлагодар€ этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый дл€ обработки результатов наблюдений.
¬ спорте по шкале отношений измер€ют рассто€ние, силу, скорость и дес€тки других переменных. ѕо шкале отношений измер€ют и те величины, которые образуютс€ как разности чисел, отсчитанных по шкале интервалов. “ак, календарное врем€ отсчитываетс€ по шкале интервалов, а интервалы времени Ч по шкале отношений.
ѕри использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводитс€ к экспериментальному определению отношени€ этой величины к другой подобной, прин€той за единицу. »змер€€ длину прыжка, мы узнаем во сколько раз эта длина больше длины другого тела, прин€того за единицу длины (метровой линейки в частном случае); взвешива€ штангу, определ€ем отношение ее массы к массе другого тела Ч единичной гири "килограмма" и т.п. ≈сли ограничитьс€ только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерению: измерить какую-либо величину Ч значит найти опытным путем ее отношение к соответствующей единице измерени€.
¬ таблице 3 приведены сводные сведени€ о шкалах измерени€.
“аблица 3
Ўкалы измерений.
| Ўкала | ќсновные операции | ƒопустимые математические процедуры | ѕримеры |
| Ќаименований | ”становление равенства | „исло случаев ћода оррел€ци€ случайных событий (тетра- и полихорические коэффициенты коррел€ции) | Ќумераци€ спортсменов в команде –езультаты жеребьевки |
| ѕор€дка | ”становление соотношений "больше" или "меньше" | ћедиана –ангова€ коррел€ци€ –анговые критерии ѕроверка гипотез непараметрической статистикой | ћесто, зан€тое на соревновани€х –езультаты ранжировани€ спортсменов группой экспертов |
| »нтервалов | ”становление равенства интервалов | ¬се методы статистики кроме определени€ отношений | алендарные даты (врем€) —уставной угол “емпература тела |
| ќтношений | ”становление равенства отношений | ¬се методы статистики | ƒлина, сила, масса, скорость и т.п. |
’од работы
|
|
|
«јƒј„ј 1.
ќпределить в единицах —»:
а) мощность (N) электрического тока, если его напр€жение U=1к¬, сила I=500 mA;
б) среднюю скорость (V) объекта, если за врем€ t=500 мс им пройдено рассто€ние S=10 см;
в) силу тока (I), протекающего в проводнике с сопротивлением 20 кќм, если к нему приложено напр€жение 100 м¬.
–ешение:
| N=U*I; N = |
| V=S/t; V = |
| I=U/R; I = |
¬ывод:
«јƒј„ј 2.
Ќайти точное значение становой силы, если показание станового динамометра равно Fизм=140 к√, абсолютна€ погрешность составл€ет
D F= ± 3 к√.
–ешение:

|

|
¬ывод:
«јƒј„ј 3.
ќпределить, что измерено точнее пальпаторным методом: пульс поко€ за 1 мин (р1=72 уд.) или за 10 с (р2=11 уд.), если абсолютна€ погрешность измерени€ 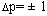 уд.
уд.
–ешение:

|
| e 1= |
| e2= |
¬ывод:
«јƒј„ј 4.
ќпределить точное значение показател€ становой силы у исследуемого, если максимальное значение шкалы станового динамометра Fmax=450 к√, класс точности прибора “ѕ=1,5%, а показанный результат Fизм=210 к√.
–ешение:

или



¬ывод:
«јƒј„ј 5.
–андомизировать показани€ своей частоты сердечных сокращений в покое, измерив ее трижды за 15 с.
–1=; р2=; р3=.
–ешение:

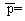
¬ывод:
онтрольные вопросы
1. ѕредмет и задачи спортивной метрологии.
2. ѕон€тие об измерении и единицах измерени€.
3. Ўкалы измерений.
4. ќсновные, дополнительные, производные единицы —».
5. –азмерность производных величин.
6. ѕон€тие о точности измерений и погрешност€х.
7. ¬иды погрешностей (абсолютна€, относительна€, систематическа€ и случайна€).
8. ѕон€тие о классе точности прибора, тарировке, калибровке и рандомизации.






