Термодинамические параметры состояния

ИНСТИТУТ ЭНЕРГЕТИКИ И АВТОМАТИКИ

Кафедра теплотехнических

И энергетических систем

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА

Магнитогорск

ВВЕДЕНИЕ...........................................................................................................................
Тема1. Предмет и метод термодинамики.....................................................................
Термодинамическая система.............................................................................
Термодинамические параметры состояния.....................................................
Уравнение состояния.........................................................................................
Термодинамический процесс..........................................................................
Теплоемкость газов...........................................................................................
Тема 2. Смеси идеальных газов....................................................................................
Аналитическое выражение первого закона термодинамики............................
Тема 3. Внутренняя энергия...........................................................................................
Работа расширения..........................................................................................
Теплота................................................................................................................
Энтальпия..............................................................................................................
Энтропия..............................................................................................................
Тема 4. Общая формулировка второго закона..............................................................
Прямой цикл Карно..............................................................................................
Обратный цикл Карно.........................................................................................
Изменение энтропии в неравновесных процессах...........................................
Тема 5. Термодинамические процессы идеальных газов в закрытых системах.........
Эксергия................................................................................................................
Тема 6. Термодинамические процессы реальных газов................................................
Уравнение состояния реальных газов...............................................................
Тема 7. Уравнение первого закона термодинамики для потока...................................
Истечение из суживающегося сопла..................................................................
Основные закономерности течения газа в соплах и диффузорах...................
Расчет процесса истечения с помощью h-s диаграммы....................................
Дросселирование газов и паров..........................................................................
Тема 8. Термодинамическая Эффективность циклов теплосиловых установок.........
Циклы поршневых двигателей внутреннего сгорания....................................
Циклы газотурбинных установок.......................................................................
Циклы паротурбинных установок....................................................................
Циклы Карно и Ренкина насыщенного пара. Регенерация теплоты...............
Цикл Ренкина на перегретом паре......................................................................
Термический КПД цикла....................................................................................
Теплофикация.......................................................................................................

Тема 9. Теоретический процесс многоступенчатого компрессора

. Контрольные вопросы для проведения промежуточной аттестации (экзамена) по итогам освоения дисциплины:

Сущность и формулировки первого закона термодинамики.
Аналитическое выражение первого закона термодинамики.
Показать на P – V диаграмме полезную работу и работу расширения (сжатия) для произвольного термодинамического процесса.
Внутренняя энергия и энтальпия как функции состояния, их связь с теплоемкостью.
Что называется полной теплоемкостью.
Удельная теплоемкость – массовая, объемная и мольная, их обозначение и размерность.
Какая теплоемкость больше – изобарная или изохорная и почему.
Основные термодинамические процессы, их изображение на P–V и T–S диаграммах.
Соотношение параметров для основных термодинамических процессов.
Расчет адиабатного процесса с помощью функций  ₀ и  _0.
Обратимые и необратимые процессы, основные причины необратимости.
Изобразить на T – S диаграмме обратимый и необратимый адиабатный процесс расширения и сжатия.
Сущность и формулировки второго закона термодинамики.
Аналитическое выражение второго закона термодинамики для обратимых и необратимых процессов.
Энтропия как функция состояния, физический смысл энтропии.
Что называется термодинамическим циклом.
Прямые и обратные термодинамические циклы.
Как оценить эффективность прямого и обратного цикла.
Принципиальная схема теплового двигателя и холодильной установки.
Прямой цикл Карно, его термический КПД, изображение на диаграммах состояния.
Реальные газы, уравнение состояния Ван – дер – Ваальса.
Фазовая P – T диаграмма для нормального и аномального вещества.
Показать на T–S диаграмме затраченную на парообразование теплоту.
Водяной пар – насыщенный (сухой и влажный) и перегретый – определения.
Диаграммы состояния водяного пара P – V, T – S, h – S.
Критическая и тройная точки.
Термодинамические прцессы водяного пара на диаграммах состояния.

28.Уравнение первого закона термодинамики для потока рабочего тела.

29.Как рассчитать скорость истечения и расход газа через сопло.

30.Как определить профиль канала.

31.Какое сопло необходимо для получения сверхзвуковой скорости.

32.Какой процесс называется дросселированием.

33.Изобразить процесс дросселирования на h – s диаграмме.

34.Как изменяются параметры рабочего тела в процессе дросселирования.

35.Какой из трех процессов сжатия в компрессоре (изотермический, адиабатный, политропный) является наиболее выгодным и почему.

36. Многоступенчатое сжатие, его приемущества по сравнению с одноступенчатым компрессором.

37. Циклы двигателей внутреннего сгорания, их сравнение.

38. Циклы газотурбинных установок, их сравнение.

39. Методы повышения эффективности газотурбинных установок.

40.Цикл Карно для водяного пара.

41. Принципиальная схема паротурбинной установки.

42. Цикл Ренкина с насыщенным паром, его термический КПД.

43. Цикл Ренкина с перегретым паром, его термический КПД.

44. Действительный цикл Ренкина, определение абсолютного внутреннего КПД.

45. Влияние начальных и конечных параметров пара на термический КПД.

46. Схема и цикл паротурбинной установки с промежуточным перегревом пара.

47. Написать формулу термического КПД цикла с промежуточным перегревом.

48. Какой цикл называется регенеративным.

49. Схема и цикл паротурбинной установки с регенеративными отборами.

50. Написать формулу термического КПД регенеративного цикла.

51. Термодинамические основы теплофикации.

52. Коэффициент использования теплоты (КИТ).

53. Циклы атомных станций, перспективы использования атомной энергии.

54. Бинарные циклы (паро – паровые и паро – газовые).

55. Расчет термического КПД бинарных установок.

56. Безмашинное (прямое) преобразование тепловой энергии в электрическую.

57. Схема, цикл и термический КПД установки с МГД – генераторами.

58. Холодильные установки – газовые и парокомпрессионные.

59.Что называется тепловым насосом, как оценить его эффективность.

60.Первый и второй законы термодинамики для химических систем

ТЕМА 1

Предмет и метод термодинамики

Термодинамика изучает законы превращения энергии в различных процессах, происходящих в макроскопических системах и сопровождающихся тепловыми эффектами. Макроскопической системой называется любой материальный объект, состоящий из большого числа частиц. Размеры макроскопических систем несоизмеримо больше размеров молекул и атомов.

В зависимости от задач исследования рассматривают техническую или химическую термодинамику, термодинамику биологических систем и т. д. Техническая термодинамика изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих в этих превращениях.. На ее основе осуществляют расчет и проектирование всех тепловых двигателей, а также всевозможного технологического оборудования.

Рассматривая только макроскопические системы, термодинамика изучает закономерности тепловой формы движения материи, обусловленные наличием огромного числа непрерывно движущихся и взаимодействующих между собой микроструктурных частиц (молекул, атомов, ионов).

Физические свойства макроскопических систем изучаются статистическими термодинамическим методами. Статистический метод основан на использовании теории вероятностей и определенных моделей строения этих систем и представляет собой содержание статистической физики. Термодинамический метод не требует привлечения модельных представлений о структуре вещества и является феноменологическим (т. е. рассматривает «феномены» — явления в целом).

При этом все основные выводы термодинамики можно получить методом дедукции, используя только два основных эмпирических закона термодинамики.

В дальнейшем исходя из термодинамического метода мы будем для наглядности использовать молекулярно-кинетические представления о структуре вещества.

Термодинамическая система

Термодинамическая система представляет собой совокупность материальных тел, находящихся в механическом и тепловом взаимодействиях друг с другом и с окружающими систему внешними телами («внешней средой»).

Выбор системы произволен и диктуется условиями решаемой задачи. Тела, не входящие в систему, называют окружающей средой. Систему отделяют от окружающей среды контрольной поверхностью (оболочкой). Так, например, для простейшей системы — газа, заключенного в цилиндре под поршнем, внешней средой является окружающий воздух, а контрольными поверхностями служат стенки цилиндра и поршень.

Механическое и тепловое взаимодействия термодинамической системы осуществляются через контрольные поверхности. При механическом взаимодействии самой системой или над системой совершается работа. (В общем случае на систему могут действовать также электрические, магнитные и другие силы, под воздействием которых система будет совершать работу. Эти виды работ также могут быть учтены в рамках термодинамики, но нами в дальнейшем рассматриваться не будут). В нашем примере механическая работа производится при перемещении поршня и сопровождается изменением объема. Тепловое взаимодействие заключается в переходе теплоты между отдельными телами системы и между системой и окружающей средой. В рассматриваемом примере теплота может подводиться к газу через стенки цилиндра.

В самом общем случае система может обмениваться со средой и веществом (массообменное взаимодействие). Такая система называется открытой. Потоки газа или пара в турбинах и трубопроводах — примеры открытых систем. Если вещество не проходит через границы системы, то она называется закрытой. В дальнейшем, если это специально не оговаривается, мы будем рассматривать закрытые системы.

Термодинамическую систему, которая не может обмениваться теплотой с окружающей средой, называют теплоизолированной или адиабатной. Примером адиабатной системы является газ, находящийся в сосуде, стенки которого покрыты идеальной тепловой изоляцией, исключающей теплообмен между заключенным в сосуде газом и окружающими телами. Такую изоляционную оболочку называют адиабатной. Система, не обменивающаяся с внешней средой ни энергией, ни веществом, называется изолированной (или замкнутой).

Простейшей термодинамической системой является рабочее тело, осуществляющее взаимное превращение теплоты и работы. В двигателе внутреннего сгорания, например, рабочим телом является приготовленная в карбюраторе горючая смесь, состоящая из воздуха и паров бензина.

Термодинамические параметры состояния

Свойства каждой системы характеризуются рядом величин, которые принято называть термодинамическими параметрами. Рассмотрим некоторые из них, используя при этом известные из курса физики молекулярно-кинетические представления об идеальном газе как о совокупности молекул, которые имеют исчезающе малые размеры, находятся в беспорядочном тепловом движении и взаимодействуют друг с другом лишь при соударениях.

Давление обусловлено взаимодействием молекул рабочего тела с поверхностью и численно равно силе, действующей на единицу площади поверхности тела по нормали к последней. В соответствии с молекулярно-кинетической теорией давление газа определяется соотношением

, (1.1)

где F- сила; f- поверхность; n — число молекул в единице объема;

т — масса молекулы; с² — средняя квадратическая скорость поступательного движения молекул.

В Международной системе единиц (СИ) давление выражается в паскалях (1 Па=1 Н/м²). Поскольку эта единица мала, удобнее использовать 1 кПа = 1000 Па и 1 МПа=10⁶ Па.

Давление измеряется при помощи манометров, барометров и вакуумметров.

Жидкостные и пружинные манометры измеряют избыточное давление, представляющее собой разность между полным или абсолютным давлением р измеряемой среды и атмосферным давлением p атм, т.е.

Приборы для измерения давлений ниже атмосферного называются вакуумметрами; их показания дают значение разрежения (или вакуума):

, т. е. избыток атмосферного давления над абсолютным.

Следует отметить, что параметром состояния является абсолютное давление. Именно оно входит в термодинамические уравнения.

Температурой называется физическая величина, характеризующая степень нагретости тела. Понятие о температуре вытекает из следующего утверждения: если две системы находятся в тепловом контакте, то в случае неравенства их температур они будут обмениваться теплотой друг с другом, если же их температуры равны, то теплообмена не будет.

С точки зрения молекулярно-кинетических представлений температура есть мера интенсивности теплового движения молекул. Ее численное значение связано с величиной средней кинетической энергии молекул вещества:

В системе СИ единицей температуры является кельвин (К); на практике широко применяется градус Цельсия (°С). Соотношение между абсолютной Т и стоградусной I температурами имеет вид

.

В промышленных и лабораторных условиях температуру измеряют с помощью жидкостных термометров, пирометров, термопар и других приборов.

Удельный объем v — это объем единицы массы вещества. Если однородное тело массой М занимает объем v, то по определению

v = V/М.

В системе СИ единица удельного объема 1 м³/кг. Между удельным объемом вещества и его плотность существует очевидное соотношение:

Для сравнения величин, характеризующих системы в одинаковых состояниях, вводится понятие «нормальные физические условия»:

p =760 мм рт.ст.= 101,325 кПа; T =273,15 K.

В разных отраслях техники и разных странах вводят свои, несколько отличные от приведенных «нормальные условия», например, «технические» (p = 735,6 мм рт.ст.= 98 кПа, t =15˚C) или нормальные условия для оценки производительности компрессоров (p =101,325 кПа, t =20˚С) и т. д.

Если все термодинамические параметры постоянны во времени и одинаковы во всех точках системы, то такое состояние системы называется равновесным.

Если между различными точками в системе существуют разности температур, давлений и других параметров, то она является неравновесной. В такой системе под действием градиентов параметров возникают потоки теплоты, вещества и другие, стремящиеся вернуть ее в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в состояние равновесия и никогда самопроизвольно выйти из него не может. В классической термодинамике рассматриваются только равновесные системы.

Уравнение состояния

Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которая называется уравнением состояния. Опыт показывает, что удельный объем, температура и давление простейших систем, которыми являются газы, пары или жидкости, связаны термическим уравнением состояния вида .

Уравнению состояния можно придать другую форму:

Эти уравнения показывают, что из трех основных параметров, определяющих состояние системы, независимыми являются два любых.

Для решения задач методами термодинамики совершенно необходимо знать уравнение состояния. Однако оно не может быть получено в рамках термодинамики и должно быть найдено либо экспериментально, либо методами статистической физики. Конкретный вид уравнения состояния зависит от индивидуальных свойств вещества.

Уравнение состояния идеальных газов

Из уравнений (1.1) и (1.2) следует, что .

Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следовательно, , получим: .

Постоянную величину Nk, отнесенную к 1 кг газа, обозначают буквой R и называют газовой постоянной. Поэтому

, или . (1.3)

Полученное соотношение представляет собой уравнение Клапейрона.

Умножив (1.3) на М, получим уравнение состояния для произвольной массы газа М:

. (1.4)

Уравнению Клапейрона можно придать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молекулярной массе μ. Положив в (1.4) М= μ и V=V μ, получим для одного моля уравнение Клапейрона — Менделеева:

Здесь — объем киломоля газа, а — универсальная газовая постоянная.

В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех идеальных газов, при нормальных физических условиях равен 22,4136 м³, поэтому

Газовая постоянная 1 кг газа составляет .

Уравнение состояния реальных газов

В реальных газах в отличие от идеальных существенны силы межмолекулярных взаимодействий (силы притяжения, когда молекулы находятся на значительном расстоянии, и силы отталкивания при достаточном сближении их друг с другом) и нельзя пренебречь собственным объемом молекул.

Наличие межмолекулярных сил отталкивания приводит к тому, что молекулы могут сближаться между собой только до некоторого минимального расстояния. Поэтому можно считать, что свободный для движения молекул объем будет равен , где b — тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а следовательно, и давление увеличивается по сравнению с идеальным газом в отношении , т. е.

Силы притяжения действуют в том же направлении, что и внешнее давление, и приводят к возникновению молекулярного (или внутреннего) давления. Сила молекулярного притяжения каких-либо двух малых частей газа пропорциональна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекулярное давление обратно пропорционально квадрату удельного объема газа: рмол = а/ v ², где а — коэффициент пропорциональности, зависящий от природы газа.

Отсюда получаем уравнение Ван-дер-Ваальса (1873 г.):

или

При больших удельных объемах и сравнительно невысоких давлениях реального газа уравнение Ван-дер-Ваальса практически вырождается в уравнение состояния идеального газа Клапейрона, ибо величина a / v ²

(по сравнению с p) и b (по сравнению с v) становятся пренебрежимо малыми.

Уравнение Ван-дер-Ваальса с качественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всегда согласуются с экспериментальными данными. В ряде случаев эти отклонения объясняются склонностью молекул реального газа к ассоциации в отдельные группы, состоящие из двух, трех и более молекул. Ассоциация происходит вследствие несимметричности внешнего электрического поля молекул. Образовавшиеся комплексы ведут себя как самостоятельные нестабильные частицы. При столкновениях они распадаются, затем вновь объединяются уже с другими молекулами и т. д. По мере повышения температуры концентрация комплексов с большим числом молекул быстро уменьшается, а доля одиночных молекул растет. Большую склонность к ассоциации проявляют полярные молекулы водяного пара.

Термодинамический процесс

Изменение состояния термодинамической системы во времени называется термодинамическим процессом. Так, при перемещении поршня в цилиндре объём, а с ним давление и температура находящегося внутри газа будут изменяться, будет совершаться процесс расширения или сжатия газа.

Как уже отмечалось, система, выведенная из состояния равновесия, и предоставленная при постоянных параметрах окружающей среды самой себе, через некоторое время вновь придет в равновесное состояние, соответствующее этим параметрам. Такое самопроизвольное (без внешнего воздействия) возвращение системы в состояние равновесия

называется релаксацией, а промежуток времени, в течение которого система возвращается в состояние равновесия, называется временем релаксации. Для разных процессов он различно: если для установления равновесного давления в газе требуется всегда, то для выравнивания температуры в объеме того же газа нужны десяти; минут, а в объеме нагреваемого твердой тела — иногда несколько часов.

Термодинамический процесс называется равновесным, если все параметры системы при его протекании меняются достаточно медленно по сравнению с соответствующим процессом релаксации. В этом случае система фактически все время находится в состоянии равновесия с окружающей средой, чем и определяется название процесса.

Чтобы процесс был равновесным, скорость изменения параметров системы должна удовлетворять соотношению

где А — параметр, наиболее быстро изменяющийся в рассматриваемом процессе; с _рел — скорость изменения этого параметра в релаксационном процессе; τ рел — время релаксации.

Рассмотрим, например, процесс сжатия газа в цилиндре. Если время смещения поршня от одного положения до другого существенно превышает время релаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объему цилиндра.

Это выравнивание обеспечивается непрерывным столкновением молекул, в результате чего подводимая от поршня к газу энергия достаточно быстро и равномерно распределяется между ними. Если последующие смещения поршня будут происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным. Таким образом, равновесный процесс состоит из непрерывного ряда последовательных состояний равновесия, поэтому в каждой его точке состояние термодинамической системы можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процессами. Они являются удобной идеализацией реальных процессов, позволяющей во многих случаях существенно упростить решение задачи. Такая идеализация вполне обоснована, так как условие (1.8) выполняется на практике достаточно часто. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа и цилиндре будет равновесным, если скорость перемещения поршня много меньше скорости звука.

Процессы, не удовлетворяющие условию , протекают с нарушением равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа температура имеет различные значения.

Теплоемкость газов

Отношение количества теплоты , полученного телом при бесконечно малом изменении его состояния, к связанному с этим изменению температуры тела , называется теплоемкостью тела в данном процессе:

Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:

удельную массовую теплоемкость c, отнесенную к 1 кг газа,

Дж/(кг·К);

удельную объемную теплоемкость c´, отнесенную к количеству газа, содержащегося в 1 м³ объема при нормальных физических условиях, Дж/(м³·К);

удельную мольную теплоемкость 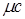, отнесенную к одному киломолю, Дж/(кмоль·К).

Зависимость между удельными теплоемкостями устанавливается очевидными соотношениями: ;

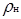Здесь — плотность газа при нормальных условиях.

Изменение температуры тела при одном и том же количестве сообщаемой теплоты зависит от характера происходящего при этом процесса, поэтому теплоемкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 К различного количества теплоты. Численно величина с изменяется в пределах от +∞ до -∞.

В термодинамических расчетах большое значение имеют:

теплоемкость при постоянном давлении

равная отношению количества теплоты , сообщенной телу в процессе при постоянном давлении, к изменению температуры тела dT

теплоемкость при постоянном объеме

, (1.5)

равная отношению количества теплоты, подведенной к телу в процессе при постоянном объеме, к изменению температуры тела.

В соответствии с первым законом термодинамики для закрытых систем, в которых протекают равновесные процессы , и

Для изохорного процесса (v =const) это уравнение принимает вид , и, учитывая (1.5), получаем, что

т. е. теплоемкость тела при постоянном объеме равна частной производной от его внутренней энергии по температуре и характеризует темп роста внутренней энергии в изохорном процессе с увеличением температуры.

Для идеального газа

Для изобарного процесса из уравнения (2.16) и (2.14) получаем

или

Это уравнение показывает связь между теплоемкостями с_р и сv. Для идеального газа оно значительно упрощается. Действительно, внутренняя энергия идеального газа определяется только его температурой и не зависит от объема, поэтому и, кроме того, из уравнения состояния следует , откуда

Это соотношение называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов.

В процессе v =const теплота, сообщаемая газу, идет лишь на изменение его внутренней энергии, тогда как в процессе р = const теплота расходуется и на увеличение внутренней энергии и на совершение работы против внешних сил. Поэтому с_р больше сv на величину этой работы.

Для реальных газов , поскольку при их расширении (при p =const) совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты.

Обычно теплоемкости определяются экспериментально, но для многих веществ их можно рассчитать методами статистической физики.

Результаты классической теории теплоемкости достаточно хорошо согласуются с экспериментальными данными в области комнатных температур (табл. 2.1), однако основной вывод о независимости от температуры эксперимент не подтверждает. Расхождения, особенно существенные в области низких и достаточно высоких температур, связаны с квантовым поведением молекул и находят объяснения в рамках квантовой теории теплоемкости.

Теплоемкость некоторых газов при t= 0°С в идеально-газовом состоянии

Газ	Число степеней свободы	Мольная теплоемкость, кДж/кмольК	k = с_р /сv
Гелий Не		12,60	1,660
Аргон Аг		12,48	1,660
Кислород 0₂		20,96	1,397
Водород Н2		20,30	1,410
Азот М₂		20,80	1,400
Метан СН₄		26,42	1,315
Аммиак ЫН₃		26,67	1,313
Диоксид угле- рода СО2		27,55	1,302

Эта теория устанавливает, прежде всего, несправедливость теоремы о равномерном распределении энергии по степени свободы в области низких и высоких температур. С уменьшением температуры газа происходит «вымораживание» числа степеней свободы молекулы. Так, для двухатомной молекулы происходит «вымораживание» вращательных степеней свободы и она вместо пяти имеет три степени свободы, а следовательно, и меньшую внутреннюю энергию и теплоемкость. С увеличением температуры у многоатомных молекул происходит возбуждение внутренних степеней свободы за счет возникновения колебательного движения атомов молекулы (молекула становится осциллятором). Это приводит к увеличению внутренней энергии, а следовательно, и теплоемкости с ростом температуры.

Теплоемкость реального газа зависит от давления, правда, очень слабо.

Поскольку теплоемкость реального газа зависит от температуры, в термодинамике различают истинную и среднюю теплоемкости.

Средней теплоемкостью с _ср данного процесса в интервале температур от t1 до t2 называется отношение количества теплоты, сообщаемой газу, к разности конечной и начальной температур:

Выражение

определяет теплоемкость при данной температуре или так называемую истинную теплоемкость. Из * следует, что

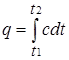
поэтому

Для практических расчетов теплоемкости всех веществ сводят в таблицы, причем с целью сокращения объема таблиц средние теплоемкости приводят в них для интервала температур от 0 до t.

ЛЕКЦИЯ 2

Смеси идеальных газов

Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газовую постоянную, молекулярную массу и теплоемкость смеси.

Закон Дальтона. В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и паровых котлов, влажный воздух в сушильных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в нее компонентов:

Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси. Состав газовой смеси может быть задан массовыми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

Очевидно, что и .

Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .

Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .

Приведенным называется объем, который занимал бы компонент газа, если бы его давление и температура равнялись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состояния i -го компонента:

; (2.1)

Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает полный объем смеси, а второе уравнение — к приведенному состоянию, когда давление и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона ,откуда . Объемные доли также часто задаются в процентах. Для воздуха , .

Иногда бывает удобнее задать состав смеси мольными долями. Мольной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей второго компонента и т. д. Число молей смеси , а мольная доля компонента будет равна .

В соответствии с законом Авогадро объемы моля любого газа при одинаковых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компонента, т. е. а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.

Газовая постоянная смеси газов. Просуммировавуравнения (2.1) для всех компонентов смеси, получим 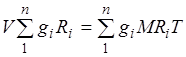. Учитывая , можно записать

, (2.3)

где

. (2.4)

Из уравнения (2.3) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона. Поскольку то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид

(2.5)

Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси : (2.6)

Сравнивая правые части соотношений (2.5) и (2.6), найдем

Изопределения массовых долей следует, что

Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:

. (2.7)

Соотношение между объемными и массовыми долями. Учитывая (2.7), получаем .

Поскольку , то

Разделив числитель и знаменатель этой формулы на массу смеси М, получим

Аналитическое выражение первого закона термодинамики

Первый закон термодинамики представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к тепловым явлениям. В соответствии с уравнением Эйнштейна надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон сохранения энергии можно рассматривать независимо.

Закон сохранения и превращения энергии является фундаментальным законом природы, который получен на основе обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утверждает, что энергия не исчезает и не возникает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.

В числе первых ученых, утверждавших принцип сохранения материи и энергии, был наш соотечественник М. В. Ломоносов (1711 — 1765 гг.).

Пусть некоторому рабочему телу с объемом V и массой М, имеющему температуру Т и давление р, сообщается извне бесконечно малое количество теплоты . В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.

Повышение температуры тела свидетельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциальной энергии частиц. В результате внутренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него давление, то при расширении оно производит механическую работу против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии

(2.8)

т. е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.

Полученное уравнение является математическим выражением первого закона термодинамики. Каждый из трех членов этого соотношения может быть положительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.

1. — теплообмен системы с окружающей средой отсутствует, т. е. теплота к системе не подводится и от нее не отводится. Процесс без теплообмена называется адиабатным. Для него уравнение (2.8) принимает вид:

Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабатном сжатии рабочего тела затрачиваемая извне работа целиком идет на увеличение внутренней энергии системы.

2. — при этом объем тела не изменяется, dV =0. Такой процесс называется изохорным, для него

т. е. количество теплоты, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.

3. dU=0 – внутренняя энергия системы не изменяется и

т.е. сообщаемая системе теплота превращается в эквивалентную ей внешнюю работу.

Для системы, содержащей 1 кг рабочего тела

. (2.9)

Проинтегрировав уравнения (2.8) и (2.9) для некоторого процесса, получим выражение первого закона термодинамики в интегральной форме:

; .

ЛЕКЦИЯ 3

Внутренняя энергия

Внутренняя энергия системы включает в себя:

кинетическую энергию поступательного, вращательного и колебательного движения частиц;

потенциальную энергию взаимодействия частиц;

энергию электронных оболочек атомов;

внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в дальнейшем под внутренней энергией будем понимать энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул является функцией температуры, значение потенциальной энергии зависит от среднего расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. Поэтому внутренняя энергия U есть функция состояния тела.

Для сложной системы она определяется суммой энергий отдельных частей, т. е. обладает свойством аддитивности. Величина и=U/М, называемая удельной внутренней энергией (Дж/кг), представляет собой внутреннюю энергию единицы массы вещества.

В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она может быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

; ; .

Ее изменение в термодинамическом процессе не зависит от характера процесса и определяется только начальным и конечным состояниями тела:

;

— значение внутренней энергии в начальном состоянии, а — в конечном. Математически это означает, что бесконечно малое изменение внутренней энергии du есть полный дифференциал и; если выразить внутреннюю энергию в виде функции удельного объема и температуры, то

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от объема газа или давления , а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

Для задач технической термодинамики важно не абсолютное значение внутренней энергии, а ее изменение в различных термодинамических процессах. Поэтому начало отсчета внутренней энергии может быть выбрано произвольно. Например, в соответствии с международным соглашением для воды за нуль принимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при 0 °С вне зависимости от давления.

Работа расширения

Работа в термодинамике, так же как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.

Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ действует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки: .

Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности: , следовательно

. (3.1)

При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, равна

Из (3.1) следует, что и dV всегда имеют одинаковые знаки:

если dV>0, то и >0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;

если же dV<0, то и <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ является джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим

l = L/M; .

Величина, представляющая собой удельную работу, совершаемую системой, содержащей 1 кг газа, равна

. (3.2)

Поскольку в общем случае р — величина переменная, то интегрирование возможно лишь тогда, когда известен закон изменения давления р = р(v).

Формулы (3.1) — (3.2) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко используют р,v – диаграмму, в которой осью абсцисс служит удельный объем, а осью ординат — давление. Поскольку состояние термодинамической системы определяется двумя параметрами, то на р,v – диаграмме оно изображается точкой. На рисунке точка 1 соответствует начальному состоянию системы, точка 2 — конечному, а линия 12 — процессу расширения рабочего тела от v1 до v2. При бесконечно малом изменении объема площадь заштрихованной вертикальной полоски равна ; следовательно, работа процесса 12 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами.

Таким образом, работа изменения объема эквивалентна площади под кривой процесса в диаграмме р, v (рисунок 3.1).

Рисунок 3.1 - Графическое изображение работы в р, v – координатах

Каждому пути перехода системы из состояния / в состояние 2 (например, 12, 1а2 или 1b2) соответствует своя работа расширения.Следовательно, работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояний системы. С другой стороны, зависит от пути интегрирования и, следовательно, элементарная работа не является полным дифференциалом.

Работа всегда связана с перемещением макроскопических тел в пространстве, например перемещением поршня, деформацией оболочки, поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от одного тела к другому и является мерой переданной энергии. Поскольку величина пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные продукты сгорания того или иного топлива.

Теплота

Помимо макрофизической формы передачи энергии — работы существует также и микрофизическая, т. е. осуществляемая на молекулярном уровне форма обмена энергией между системой и окружающей средой. В этом случае энергия может быть передана системе без совершения работы. Мерой количества энергии, переданной микрофизическим путем, служит теплота.

Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвекцией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности температур между телами.

Как будет показано ниже, элементарное количество теплоты , так же как и L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.

Внутренняя энергия — это свойство самой системы, она характеризует состояние системы. Теплота и работа — это энергетические характеристики процессов механического и теплового взаимодействий системы с окружающей средой. Они характеризуют те количества энергии, которые переданы системе или отданы ею через ее границы в определенном процессе.

Энтальпия

В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:

; ; ,

а величина dh является полным дифференциалом.

Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.

Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G.

Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил: . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: . Получаем, что , т.е. энтальпию можно трактовать как энергию расширенной системы.

Уравнение в случае, когда единственным видом