“еори€
олебани€ Ц это движени€ или процессы, которые характеризуютс€ определенной повтор€емостью во времени.
олебани€, которые совершаютс€ за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему, называютс€ свободными (собственными) колебани€ми.
олебани€, при которых колеблюща€с€ величина измен€етс€ со временем по закону синуса или косинуса, называютс€ гармоническими.
”равнени€ гармонических колебаний 
где ј - амплитуда колебаний (максимально значение колеблющейс€ величины), ω- кругова€ (циклическа€) частота,  - начальна€ фаза в момент времени t = 0,
- начальна€ фаза в момент времени t = 0,  - фаза колебаний в момент времени t; s Ц сме-щение колеблющейс€ величины
- фаза колебаний в момент времени t; s Ц сме-щение колеблющейс€ величины
ѕериод гармонического колебани € Ц промежуток времени “, в течение которого фаза колебани€ получает приращение 2 π  или
или 
„астота колебаний Ц число полных колебаний, совершаемых в единицу времени.
 или
или 
—корость колеблющейс€ точки - 
”скорение колеблющейс€ точки - 

—ила, действующа€ на колеблющуюс€ материальную точку
инетическа€ энерги€ 
ѕотенциальна€ энерги€ 
ѕолна€ энерги€ 
¬ынужденными колебани€ми называютс€ незатухающие колебани€ системы, которые вызываютс€ действием на нее внешних сил F(t), периодически измен€ющихс€ с течением времени. —ила F(t), вызывающа€ вынужденные колебани€, называютс€ вынужденной силой.
¬ынужденными €вл€ютс€ колебани€ силы тока в сети переменного тока, колебани€ гребных винтов, лопаток и валов турбин под действием периодически измен€ющихс€ внешних сил. ≈сли сила F(t) измен€етс€ по закону  , где F0 -амплитуда возмущающей силы, а
, где F0 -амплитуда возмущающей силы, а  -ее циклическа€ частота, то в системе, на которую действует така€ сила, могут установитьс€ вынужденные колебани€, которые €вл€ютс€ также гармоническими, происход€т с циклической частотой, равной частоте
-ее циклическа€ частота, то в системе, на которую действует така€ сила, могут установитьс€ вынужденные колебани€, которые €вл€ютс€ также гармоническими, происход€т с циклической частотой, равной частоте  вынуждающей силы, и описываютс€ уравнением
вынуждающей силы, и описываютс€ уравнением  , где ј Ц амплитуда вынужденных колебаний физической величины (например, смещени€),
, где ј Ц амплитуда вынужденных колебаний физической величины (например, смещени€),  - разность фаз между вынужденными колебани€ми x и силой F(t).
- разность фаз между вынужденными колебани€ми x и силой F(t).
јмплитуда ј установившихс€ вынужденных колебаний определ€етс€ по формуле:
 ,
,
где F0 -амплитуда вынужденной силы, m Ц масса колеблющейс€ системы,  - циклическа€ частота свободных незатухающих колебаний системы,
- циклическа€ частота свободных незатухающих колебаний системы,  - циклическа€ частота внешней силы,
- циклическа€ частота внешней силы,  - коэффициент затухани€. ѕри посто€нных F0, m и
- коэффициент затухани€. ѕри посто€нных F0, m и  амплитуда вынужденных колебаний зависит от соотношени€ частот вынужденной силы (
амплитуда вынужденных колебаний зависит от соотношени€ частот вынужденной силы ( ) и свободных незатухающих колебаний (
) и свободных незатухающих колебаний ( ). √рафик зависимости амплитуды ј от
). √рафик зависимости амплитуды ј от  при различных коэффициентах затухани€, приведены на рис.
при различных коэффициентах затухани€, приведены на рис.
јнализ формулы дл€ амплитуды ј вынужденных колебаний:
а) если циклическа€ частота вынуждающей силы равна нулю ( =0), то
=0), то  ; при этом колебани€ не совершаютс€ и отклонение системы из положени€ равновеси€ называетс€ систематическим отклонением;
; при этом колебани€ не совершаютс€ и отклонение системы из положени€ равновеси€ называетс€ систематическим отклонением;
б) при отсутствии затухани€ ( =0) амплитуда вынужденных колебаний растет с увеличением
=0) амплитуда вынужденных колебаний растет с увеличением  , и при
, и при  =
=  , когда знаменатель в формуле дл€ ј становитс€ равным нулю, амплитуда колебаний стремитс€ к бесконечности; при дальнейшем росте частоты ј уменьшаетс€
, когда знаменатель в формуле дл€ ј становитс€ равным нулю, амплитуда колебаний стремитс€ к бесконечности; при дальнейшем росте частоты ј уменьшаетс€  ;
;
|
|
|
в) если затухание существует  , то амплитуда вынужденных колебаний достигает наибольшего значени€ при частоте
, то амплитуда вынужденных колебаний достигает наибольшего значени€ при частоте  вынуждающей силы, не совпадающей с частотой свободных незатухающих колебаний
вынуждающей силы, не совпадающей с частотой свободных незатухающих колебаний  :
:

явление возрастани€ амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к значению  называетс€ резонансом. —оответственно величина
называетс€ резонансом. —оответственно величина  называетс€ резонансной циклической частотой, а кривые зависимости ј от
называетс€ резонансной циклической частотой, а кривые зависимости ј от  - резонансными кривыми.
- резонансными кривыми.
явление резонанса используетс€ в акустике дл€ анализа звуков, их усилени€ и т.д. ѕод действием периодически измен€ющихс€ нагрузок в машинах и различных сооружени€х могут возникнуть €влени€ резонанса, которые иногда бывают опасны дл€ эксплуатации машин.
 рис.1
рис.1
II ћа€тники

ѕружинный ма€тник Ц груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебани€ под действием упругой силы
ѕружинный ма€тник совершает гармонические колебани€ с циклической частотой

где k Ц коэффициент упругости (жесткость) пружины
ѕериод колебаний

ћатематический ма€тник Ц идеализированна€ система, состо€ща€ из материальной точки массой m, подвешенной на нераст€жимой невесомой нити, и колеблющейс€ под действием силы т€жести.
ѕриближением математического ма€тника €вл€етс€ небольшой т€желый шарик, подвешенный на тонкой длинной нити.
ѕериод малых колебаний математического ма€тника

(l - длина ма€тника)
‘изический ма€тник Ц твердое тело, совершающее под действием силы т€жести колебани€ вокруг неподвижной горизонтальной оси подвеса, не проход€щей через центр масс тела.
III ¬олны
—реда называетс€ упругой, если между ее частицами существуют силы взаимодействи€, преп€тствую-щие какой-либо деформации этой среды.
≈сли какое-либо тело совершает колебани€ в упругой среде, то оно воздействует на частицы среды, прилегающие к телу, и заставл€ет их совершать вынужденные колебани€. —реда вблизи колеблющегос€ тела деформируетс€ и в ней возникают упругие силы. Ёти силы действуют на все более удаленные от тела частицы среды, вывод€ их из положени€ равновеси€. ѕостепенно все частицы среды вовлекаютс€ в колебательное движение.
¬олнами называютс€ вс€кие возмущени€ состо€ни€ вещества или пол€, распростран€ющиес€ в пространстве с течением времени. Ќапример, звуковые волны в газах или в жидкост€х представл€ют собой колебани€ давлени€, распростран€ющихс€ в этих средах.
”пругими волнами называютс€ механические возмущени€ (деформации), которые распростран€ютс€ в упругой среде. “ела, вызывающие эти возмущени€ в среде, называютс€ источниками волн (колеблющиес€ камертоны, струны музыкальных инструментов и т.д.). ”пругие волны называютс€ звуковыми или акустическими, если соответствующие им механические деформации среды имеют малые амплитуды.
ќтличие упругих волн в среде от любого другого упор€доченного движени€ ее частиц состоит в том, что распространение волн не св€зано с переносом вещества среды из одного места в другое на большие рассто€ни€.
¬олновой поверхностью (фронтом волны) называетс€ совокупность точек среды, колеблющихс€ в одинаковых фазах. Ќа волновой поверхности фазы колебаний различных точек в рассматриваемый момент времени имеют одно и то же значение.
 Ћучом называетс€ лини€, касательна€ к которой в каждой точке совпадает с направлением распространени€ волны. ¬ однородной изотропной среде луч €вл€етс€ пр€мой, перпендикул€рной к фронту волны, и совпадает с направлением переноса энергии волны.
Ћучом называетс€ лини€, касательна€ к которой в каждой точке совпадает с направлением распространени€ волны. ¬ однородной изотропной среде луч €вл€етс€ пр€мой, перпендикул€рной к фронту волны, и совпадает с направлением переноса энергии волны.
|
|
|
¬ плоской волне волновыми поверхност€ми €вл€ютс€ плоскости, перпендикул€рные к направлению распространени€ волны. Ћучами €вл€ютс€ параллельные пр€мые, совпадающие с направлением скорости распространени€ волны. “акие волны могут быть получены на поверхности воды с помощью колебаний плоского стержн€. Ќа рисунке 2 показаны фронты плоской волны и лучи.
рис. 2
 ¬олна называетс€ поперечной, если частицы среды колеблютс€ в направлени€х, перпендикул€рных к направлению распространени€ волны. Ќапример, поперечна€ волна распростран€етс€ вдоль нат€нутого резинового шара, один конец которого закреплен, а другой приведен в колебательное движение.
¬олна называетс€ поперечной, если частицы среды колеблютс€ в направлени€х, перпендикул€рных к направлению распространени€ волны. Ќапример, поперечна€ волна распростран€етс€ вдоль нат€нутого резинового шара, один конец которого закреплен, а другой приведен в колебательное движение.
рис.3
¬олна называетс€ продольной, если колебани€ частиц среды происходит в направлении распространени€ волны.
ѕродольна€ волна возникает в длинной спиральной пружине, если один конец подвергаетс€ периодически внешнему воздействию (см. рис. 4). ”пруга€ волна представл€ет собой распростран€ющиес€ вдоль пружины последовательные сжати€ и раст€жени€ ее, периодически, через врем€ T/2, смен€ющие друг друга (T Ц период внешнего воздействи€ на пружину).
 ¬ газах и жидкост€х, которые не обладают упругостью формы, распространение поперечных волн невозможно. ¬ твердых телах возможно распространение как продольных, так и поперечных волн, св€занных с наличием упругости формы (например, волны, распростран€ющиес€ вдоль струн музыкальных инструментов).
¬ газах и жидкост€х, которые не обладают упругостью формы, распространение поперечных волн невозможно. ¬ твердых телах возможно распространение как продольных, так и поперечных волн, св€занных с наличием упругости формы (например, волны, распростран€ющиес€ вдоль струн музыкальных инструментов).
—коростью распространени€ волны (фазовой скоростью) называетс€ физическа€ величина, численно равна€ рассто€нию, которое за единицу времени проходит люба€ точка волновой поверхности. ¬ектор скорости  направлен по нормали к волновой поверхности в стороны распространени€ волны и в однородной изотопной среде совпадает с направлением луча.
направлен по нормали к волновой поверхности в стороны распространени€ волны и в однородной изотопной среде совпадает с направлением луча.
—корость распространени€ энергии волн любой физической природы конечна и не может превысить скорость света в вакууме. Ёто вытекает из основных утверждений специальной теории относительности. Ќа фазовую скорость эти ограничени€ не распростран€ютс€.
—корость распространени€ упругих звуковых волн в газах зависит от термодинамической температуры газа. ƒл€ идеальных газов скорость звука
 ,
,
где R Ц универсальна€ газова€ посто€нна€, T Ц термодинамическа€ температура,  - мол€рна€ масса,
- мол€рна€ масса,  - посто€нна€ дл€ данного газа величина, завис€ща€ от строени€ молекулы газа. Ќапример, дл€ воздуха
- посто€нна€ дл€ данного газа величина, завис€ща€ от строени€ молекулы газа. Ќапример, дл€ воздуха  =1,4 и
=1,4 и 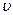 =20
=20  . ѕри T= 273 :
. ѕри T= 273 : 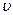 =330 м/с, при T= 293 :
=330 м/с, при T= 293 : 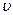 =343 м/с.
=343 м/с.
—корость упругих волн в жидкост€х и продольных волн в твердых телах превышает скорость звука в газах и зависит от сжимаемости (упругости) и плотности среды:
 ,
,
где K Ц модуль объемной упругости,  - плотность среды.
- плотность среды.
Ќапример, дл€ воды 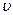 =1430 м/с, дл€ меди
=1430 м/с, дл€ меди 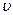 =3910 м/с, дл€ алюмини€
=3910 м/с, дл€ алюмини€ 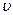 =4880 м/с.
=4880 м/с.
‘ронт волны распростран€етс€ от источника волн за врем€ на некоторое рассто€ние  , где
, где 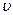 - скорость распространени€ волны. Ёто означает, что колебани€ частиц среды, отсто€щих на
- скорость распространени€ волны. Ёто означает, что колебани€ частиц среды, отсто€щих на  от источника, происход€т с запаздыванием по времени на
от источника, происход€т с запаздыванием по времени на  , а по фазе на
, а по фазе на  , причем
, причем  , поскольку за период “ колебани€ в источнике фаза измен€етс€ на
, поскольку за период “ колебани€ в источнике фаза измен€етс€ на  .
.
«апаздывание по времени  и по фазе
и по фазе  колебаний точек среды, удаленных на рассто€ние x от источника,
колебаний точек среды, удаленных на рассто€ние x от источника,
 ,
,  ,
,
где величина  - длина волны. ≈сли
- длина волны. ≈сли  , то
, то  . ƒлиной волны
. ƒлиной волны  называетс€ рассто€ние между двум€ ближайшими точками, колеблющимис€ в одинаковой фазе, т.е. со сдвигом фаз
называетс€ рассто€ние между двум€ ближайшими точками, колеблющимис€ в одинаковой фазе, т.е. со сдвигом фаз  . ћожно также сказать, что длиной волны называетс€ рассто€ние, на которое распростран€етс€ фронт волны за врем€ T, равное периоду колебаний в источнике волны (см. рис.5)
. ћожно также сказать, что длиной волны называетс€ рассто€ние, на которое распростран€етс€ фронт волны за врем€ T, равное периоду колебаний в источнике волны (см. рис.5)

—в€зь длины волны с частотой колебаний источника волн:
 ,
,
где 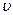 - скорость распространени€ волн,
- скорость распространени€ волн,  - частота колебаний в источнике,
- частота колебаний в источнике,  - циклическа€ частота. „астота колебаний зависит от свойств источника волн, скорость распространени€ волн и, вследствие этого, длина волны зависит от свойств среды.
- циклическа€ частота. „астота колебаний зависит от свойств источника волн, скорость распространени€ волн и, вследствие этого, длина волны зависит от свойств среды.
рис. 5
’од работы
1. ѕеречертите таблицу дл€ записи результатов измерений и вычислений.
|
|
|
| є опыта | ‘изическа€ величина | ||||
| l, см | N | t, c | T, c | ν, √ц | |
 2. ”крепите кусочек резины с вис€щим на нем ма€тником в лапке штатива, как показано на рисунке.
2. ”крепите кусочек резины с вис€щим на нем ма€тником в лапке штатива, как показано на рисунке.
ѕри этом длина ма€тника должна быть равна 5 см, как указано в таблице дл€ первого опыта. ƒлину l ма€тника измер€йте так, как показано на рисунке, т.е. от точки подвеса до середины шарика.
3. ƒл€ проведени€ первого опыта отклоните шарик от положени€ равновеси€ на небольшую амплитуду (1 - 2 см) и отпустите. »змерьте промежуток времени t, за который ма€тник совершит 30 полных колебаний. –езультаты измерений запишите в таблицу.
4. ѕроведите остальные четыре опыта так же, как и первый. ѕри этом длину l ма€тника каждый раз устанавливайте в соответствии с ее значением, указанным в таблице дл€ данного опыта.
5. ƒл€ каждого из п€ти опытов вычислите и запишите в таблицу значени€ периода T колебаний ма€тника.
6. ƒл€ каждого из п€ти опытов рассчитайте значени€ частоты ν колебаний ма€тника по формуле:  или
или  . ѕолученные результаты внесите в таблицу.
. ѕолученные результаты внесите в таблицу.
7. —делайте выводы о том, как завис€т период и частота свободных колебаний ма€тника от его длины.
«апишите эти выводы.
8. ќтветьте на вопросы. ”величили или уменьшили длину ма€тника, если:
а) период его колебаний сначала был 0,3 с, а после изменени€ длины стал 0,1 с;
б) частота его колебаний вначале была равна 5 √ц, а потом уменьшилась до 3 √ц?






