ћатематическа€ модель совместного анализа, выражающа€ фундаментальную зависимое между характеристиками и полезностью товара.
¬ажность характеристики /, определ€ют через диапазон полезностей atj по всем уровь этой характеристики:
/,. = {max (ctjj) Ч min (a^)} дл€ каждого /.
¬ажность характеристики нормируют дл€ уточнени€ ее важности относительно других рактеристик Wji
“ак что
=1.
—уществует несколько методов использовани€ базовой модели. ѕростейший и самый попу≠л€рный Ч регрессионный анализ с фиктивными (dummy) переменными (см. главу 17). ¬ этом случае вычисленные переменные состо€т из фиктивных переменных дл€ атрибутивных уров≠ней. ≈сли характеристика имеет ki уровней, ее кодируют через (&, Ч 1)-ю фиктивную перемен≠ную (см. главу 14). ≈сли получены метрические данные, то рейтинги, выраженные в интер≠вальной шкале, образуют зависимую переменную. ≈сли получены неметрические данные, то значени€ рангов можно преобразовать в 0 или 1, выполнив попарные сравнени€ между торго≠выми марками. ¬ этом случае вычисленные переменные представл€ют различи€ в атрибутив≠ных уровн€х сравниваемых торговых марок. другим процедурам, подход€щим дл€ анализа неметрических данных, относ€тс€ LINMAP, MONANOVAn LOGIT [29].
роме того, исследователь должен решить, на каком уровне проводить анализ Ч каждого респондента или агрегатном. Ќа индивидуальном уровне данные, полученные от каждого респондента, анализируют отдельно. ≈сли анализ выполн€ют на агрегатном уровне, то надо разработать процедуру дл€ группировани€ респондентов. ќбщий подход состоит в том, что≠бы сначала определить функции полезности индивидуального уровн€. «атем респондентов объедин€ют в кластеры, исход€ из сходства полезностей. ѕосле этого выполн€ют агрегатный анализ дл€ каждого кластера [30]. Ќеобходимо определить соответствующую модель дл€ вы≠числени€ параметров [31].
ћаркетологи проанализировали данные табл. 21.4 с помощью обычного регрессионного анализа на основании метода наименьших квадратов с фиктивными переменными. «ависима€ переменна€ представл€ла собой рейтинги предпочтений. Ќезависимыми переменными, или предикторами, €вл€лись шесть фиктивных переменных, по две дл€ каждой переменной. ѕре≠образованные данные приведены в табл. 21.5.
“аблица 21.5. ƒанные о кроссовках, закодированные дл€ регрессионнного анализа с фиктивными переменными
| ’арактеристики –ейтинги предпочтений ѕодошва | ¬ерх | ÷ена | ||||
| Y | X! | ’2 | ’з | ’4 | ’5 | ’е |
ѕоскольку данные принадлежали одному респонденту, анализ выполн€ли на индивиду≠альном уровне. ‘ункции полезности, определенные дл€ каждой характеристики, а также отно≠сительна€ важность характеристик приведены в табл. 21.6 [32].
|
|
|
| “аблица 21. 6. ’арактеристика | –езультаты совл Ќомер | лестного анализа ”ровень ќписание ѕолезность | важность | |
| ѕодошва | –езина | 0,778 | ||
| ѕолиуретан | - 0,556 | |||
| ѕластик | - 0,222 | 0,286 | ||
| ¬ерх | ожа | 0,445 | ||
| ѕарусина | 0,111 | |||
| Ќайлон | - 0,556 | 0,214 | ||
| ÷ена | 1,111 | |||
| 0,111 | ||||
| -1,222 | 0,500 |
ћодель дл€ вычислени€ полезности можно представить в следующем виде: U = №0 + b jXj + b^2 + bJC3 + bJC4 + bsX5 + b^6
где
Xj, X2 Ч фиктивные переменные, представл€ющие характеристику "подошва";
’3, ’4 Ч фиктивные переменные, представл€ющие характеристику "верх"; ’5, ’6 Ч фиктивные переменные, представл€ющие характеристику "цена". ƒл€ характеристики "подошва" атрибутивные уровни можно закодировать так:
| ’т | ’2 | |
| ”ровень 1 | ||
| ”ровень 2 | ||
| ”ровень 3 |
”ровни других характеристик кодируют аналогично. ћаркетологи получили следующ результаты параметров:
/>Д = 4,222,
ј; =1,000,
№2=- 0,333, £,= 1,000, 6, Ђ0,667,
£5=2,333,
V- 1,333,
ѕри условии кодировки фиктивными переменными, в которой уровень 3 €вл€етс€ баз вым, коэффициенты можно св€зать с полезност€ми. ¬ главе 17 мы объ€сн€ли, что коэффиц ент фиктивной переменной представл€ет разность полезности дл€ этого уровн€ и полезное дл€ базового уровн€. ƒл€ характеристики "подошва" получим:
„тобы найти значени€ полезностей, введем дополнительное ограничение. ѕолезность bi ражают в интервальной шкале, поэтому начало отсчета произвольное. —ледовательно, дополн: тельно накладываемое ограничение имеет вид
ail + a!2 + a!3 = ќ
Ёти уравнени€ дл€ первой характеристики, "подошвы", следующие:
a;/- Ob =1,000,
ai2~ ai3 = Ч 0,333,
ail + a!2 + a!3 = ∞'
–ешив эти уравнени€, получим:
аД = 0,778, а12 = - 0,556, а/5 = - 0,222.
ѕолезности дл€ других характеристик, приведенных в табл. 21.6, оценим аналогично. ƒл€ характеристики "верх" имеем:
Ђ27 ~ ^23 = №3>
ƒл€ третьей характеристики "цены" получим:
а31 + а32 + а33 = 0.
¬еса относительной важности вычислили, исход€ из значений полезностей, следующим образом: —умма значений полезностей = [0,778 - (-0, 556)] + [0,445 - (-0,556)] + [l,l 1 1 - (-1, 222)] = 4,668
[0.778- (-0,556)] _ 1,334 _02,, 4,668 4,668
ќтносительна€ важность характеристики "подошва"
[0,445-(-0.556)] 1,001 _ ќтносительна€ важность характеристики верх = ~ 4 668
ќтносительна€ важность характеристики "цена" :
4,668 4,668
ќценка полезностей и весов относительной важности составл€ет основу дл€ интерпретации результатов.
»нтерпретаци€ результатов
ƒл€ интерпретации результатов целесообразно построить графики функций полезности. ѕо значени€м функций полезности дл€ каждой характеристики, приведенной в табл. 21.6, по≠строены графики функций полезности, показанные на рис. 21.10.
»з данных табл. 21.6 и графиков на рис. 21.10 видно, что этот респондент предпочитае кроссовки с резиновой подошвой, затем с пластиковой, а полиуретанова€ подошва пользует≠с€ у него наименьшей попул€рностью. „то касаетс€ верха кроссовок, то здесь респондент больше всего предпочитает кожу, следом идет парусина и нейлон. ак и следовало ожидать, самое высокое значение полезности получено дл€ цены кроссовок, равной $30, а самое низ≠кое дл€ цены Ч $90. «начени€ полезности, приведенные в табл. 21.6, выражены только в ин≠тервальной шкале, начало отсчета произвольное. — точки зрени€ относительной важности характеристик на первом месте стоит цена, на втором Ч подошва, к ней тесно примыкает верх. ѕоскольку из всех характеристик дл€ данного респондента наибольшее и значител превышающее значени€ других характеристик имеет цена, этого респондента можно назвать чувствительным к цене.
|
|
|
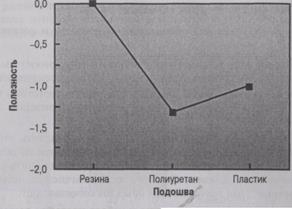

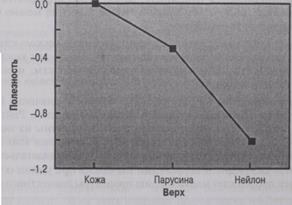 –ис. 21.10. √рафики функций полезности
–ис. 21.10. √рафики функций полезности






