ѕусть имеетс€ выборка объема n со значени€ми признака х1 х2, х3,..., хk. ѕостроим статистическое распределение.
“аблица 4
| xi | x1 | x2 | x3 | Е | xk |
| ni | n1 | n2 | n3 | Е | nk |
ƒл€ того чтобы охарактеризовать наиболее существенные свойства этого распределени€, так же как и в теории веро€тностей, используют средние показатели или, как их называют, выборочные числовые характеристики. –ассмотрим некоторые из них.
1. ¬ыборочна€ средн€€ 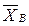 . ѕри наличии повтор€ющихс€ значений признака
. ѕри наличии повтор€ющихс€ значений признака
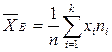 , (3)
, (3)
где п Ч объем выборки, хi ni вз€ты из табл. 4. ¬ыборочна€ средн€€ 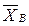 измен€етс€ при переходе от одной выборки к другой, поэтому в силу случайного отбора €вл€етс€ случайной величиной.
измен€етс€ при переходе от одной выборки к другой, поэтому в силу случайного отбора €вл€етс€ случайной величиной.
≈сли дано распределение непрерывной случайной величины, то вместо х i берут середину интервала (xi, Е, xi+1), т.е.  .
.
ƒл€ упрощени€ вычислени€ выборочных характеристик удобно перейти от данных значений признака x 1|, х2, х3,...,хk к условным значени€м и1, и2,. и3,..., uk Чпо формуле
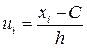 , (4)
, (4)
т. е. ввести вспомогательную величину 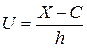 , где — Цновое начало отсчета, обычно это значение признака с наибольшей частотой, h Ц масштаб.
, где — Цновое начало отсчета, обычно это значение признака с наибольшей частотой, h Ц масштаб.
ћожно показать, что при переходе к условным значени€м признака по формуле зависимость, св€зывающа€ 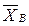 и
и 
 , имеет вид
, имеет вид
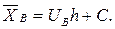 (5)
(5)
ƒействительно,
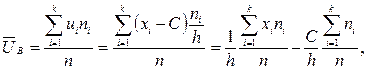
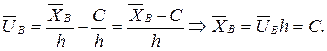
ѕример. ƒано статистическое распределение:
“аблица 5
| хi | ||||||
| ni |
Ќайти 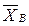 .
.
–ешение. ѕерейдем к условным значени€м признака, прин€в за C значение с наибольшей частотой, т. е. —=5. ƒалее находим h = xi - xi-1 = 2.
»меем

—оставл€ем распределение условных значений признака.
“аблица 6
| ui | Ц2 | Ц1 | ||||
| ni |
Ќаходим
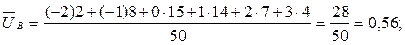

ќсобенно выгодно примен€ть формулу (4), если значени€ признака велики.
2. ¬ыборочна€ и исправленна€ дисперси€. ќдна числова€ характеристика 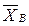 не дает полного представлени€ о статистическом распределении. ¬ агрономической и зоотехнической практике, как и в других сферах производства, при анализе результатов существенным дл€ выводов €вл€етс€ характеристика рассе€ни€ значений признака относительно выборочной средней. ќтклонение отдельных значений от выборочной средней бывает значительным и с этим нельз€ не считатьс€.
не дает полного представлени€ о статистическом распределении. ¬ агрономической и зоотехнической практике, как и в других сферах производства, при анализе результатов существенным дл€ выводов €вл€етс€ характеристика рассе€ни€ значений признака относительно выборочной средней. ќтклонение отдельных значений от выборочной средней бывает значительным и с этим нельз€ не считатьс€.
—оставим таблицу отклонений  , указыва€ соответствующие частоты.
, указыва€ соответствующие частоты.
“аблица 7
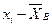
| 
| 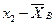
| 
| Е | 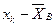
|
| ni | n1 | n2 | n3 | Е | nk |
Ќайдем среднее значение отклонений  . »меем
. »меем

—ледовательно, среднее значение отклонени€  равно нулю, и поэтому непригодно дл€ характеристики рассе€ни€ признака. ƒл€ того чтобы освободитьс€ от знака отклонени€ и при этом сделать вли€ние больших отклонений Ђболее ощутимымиї, их возвод€т в квадрат и наход€т среднее значение. ѕолученную характеристику называют выборочной дисперсией и обозначают
равно нулю, и поэтому непригодно дл€ характеристики рассе€ни€ признака. ƒл€ того чтобы освободитьс€ от знака отклонени€ и при этом сделать вли€ние больших отклонений Ђболее ощутимымиї, их возвод€т в квадрат и наход€т среднее значение. ѕолученную характеристику называют выборочной дисперсией и обозначают 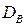 .
.
»так,
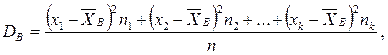
или
 (5)
(5)
ќпределение. ¬ыборочной дисперсией называетс€ среднее арифметическое значение квадратов отклонений признака от выборочной средней.
|
|
|
ѕример. ”рожайность двух сортов ј и ¬ пшеницы, возделываемых на трех участках с одинаковыми услови€ми роста и развити€, характеризуетс€ следующими таблицами:
сорт ј сорт ¬
| X, ц | Y, ц | 19 ' | ||||||
| ѕлощадь, га | ѕлощадь, га | 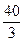
|
Ќайти дисперсии значений признака обоих сортов.
–ешение. ¬ычислим XB, YB, DX, DY. Ќаходим



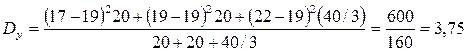
ак видим, дисперси€ Dy как мера рассе€ни€ или разброса урожайности сорта ¬ относительно среднего значени€ YB в случае примерно одинаковых площадей больше, чем Dy, а это €вление нежелательное. »з двух сортов лучшим €вл€етс€ тот, урожайность которого более устойчива. ѕо данным опыта сорт ј предпочтительнее сорта ¬.
ƒл€ вычислени€ выборочной дисперсии используют следующую формулу:
 (6)
(6)
т. е. дисперси€ равна разности между средним значением квадрата и квадратом выборочной средней.
ƒействительно,

ƒл€ облегчени€ вычислени€ дисперсии используют следующие свойства:
1∞. ƒисперси€ не изменитс€, если все значени€ признака увеличить (уменьшить) на посто€нное число.
2∞. ѕри умножении значений признака на посто€нное число h ≠ 0 дисперси€ умножаетс€ на h2.
¬ыборочна€ дисперси€, как это показано в более подробных курсах (например, [4]), имеет систематическую ошибку, привод€щую к уменьшению дисперсии. „тобы это устранить, ввод€т поправку, умножа€ DB, на  . ¬ результате получают исправленную дисперсию
. ¬ результате получают исправленную дисперсию
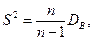 (7)
(7)
или
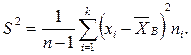 (8)
(8)
Ќа практике часто вместо этой формулы используют другую, ей равносильную, а именно:
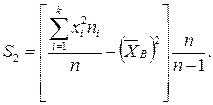 (9)
(9)
ѕри малых выборках S ощутимо отличаетс€ от DB, например, при n = 2 имеем S 2=2 DB. — возрастанием n исправленна€ дисперси€ S 2Ѓ DB. ”же при n = 30 дисперсии S 2и DB различаютс€ на 3%.






