¬ариант є 1
”гол α задан в градусах, минутах и секундах. Ќайти его величину в радианах (с максимально возможной точностью).
¬ариант є 2
”гол α задан в радианах. Ќайти его величину в градусах, минутах и секундах.
¬ариант є 3
ƒлина отрезка задана в дюймах (1 дюйм=2,54 см). ѕеревести значение длины в метрическую систему, т.е. выразить ее в метрах, сантиметрах и миллиметрах. “ак, например, 21 дюйм = 0 м 53 см 3,4 мм.
¬ариант є 4
«аданы моменты начала и конца некоторого промежутка времени в часах, минутах и секундах (в пределах одних суток). Ќайти продолжительность этого промежутка в тех же единицах измерени€.
¬ариант є 5
убическое уравнение. «аданы три корн€ кубического уравнени€: x1, x2, x3. Ќайти коэффициенты этого уравнени€.
¬ариант є 6
вадратное уравнение. Ќайти корни квадратного уравнени€, заданного своими коэффициентами, с положительным дискриминантом. ѕодстановкой в уравнение убедитьс€ в погрешности вычислений.
¬ариант є 7
омплексное число. «аданы действительна€ и мнима€ части комплексного числа z=x+ iy. ѕреобразовать его в тригонометрическую форму и напечатать в виде выражени€: z=r(cosφ+i sinφ).
ƒл€ справки:
 ;
;  .
.
¬ариант є 8
ƒвижение без топлива? ¬ладелец автомобил€ приобрел новый карбюратор, который экономит 50 % топлива, новую систему зажигани€, котора€ экономит 30 % топлива, и поршневые кольца, эконом€щие 20 % топлива. ¬ерно ли, что его автомобиль теперь сможет обходитьс€ совсем без топлива? Ќайти фактическую экономию дл€ произвольно заданных сэкономленных процентов.
¬ариант є 9
«адача жест€нщика. »з круга радиуса r вырезан пр€моугольник, больша€ сторона которого равна a. Ќайти максимальный радиус круга, который можно вырезать из этого пр€моугольника?
¬ариант є 10
ѕриближение sin x. ‘ункци€ y= sin x на отрезке  хорошо аппроксимируетс€ разложением:
хорошо аппроксимируетс€ разложением: 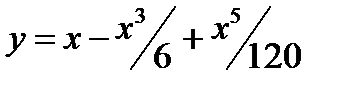 . ƒл€ заданного значени€ аргумента x вычислить y по этой формуле и сравнить с точным значением, вычисленным с помощью стандартной функции sin.
. ƒл€ заданного значени€ аргумента x вычислить y по этой формуле и сравнить с точным значением, вычисленным с помощью стандартной функции sin.
¬ариант є 11
ѕереправа. ѕловцу надо под пр€мым углом к фарватеру преодолеть реку шириной b м. ≈го скорость в сто€чей воде  ; скорость течени€ реки -
; скорость течени€ реки -  . ѕод каким углом к фарватеру он должен плыть, чтобы его Ђне снеслої? —колько времени займет переправа? ак изменитс€ решение, если посередине реки скорость пловца упадет с
. ѕод каким углом к фарватеру он должен плыть, чтобы его Ђне снеслої? —колько времени займет переправа? ак изменитс€ решение, если посередине реки скорость пловца упадет с  до
до  ?
?
¬ариант є 12
¬ершина параболы. Ќайти координаты вершины параболы 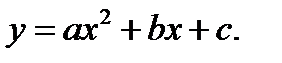
¬ариант є 13
“реугольник задаетс€ координатами своих вершин на плоскости:  ,
,  ,
,  . Ќайти площадь треугольника ABC.
. Ќайти площадь треугольника ABC.
¬ариант є 14
“реугольник задаетс€ координатами своих вершин на плоскости: 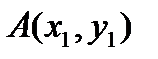 ,
,  ,
,  . Ќайти сумму длин медиан треугольника ABC.
. Ќайти сумму длин медиан треугольника ABC.
¬ариант є 15
“реугольник задаетс€ координатами своих вершин на плоскости:  ,
,  ,
,  . Ќайти точку пересечени€ биссектрис треугольника ABC (центр вписанной с него окружности).
. Ќайти точку пересечени€ биссектрис треугольника ABC (центр вписанной с него окружности).
¬ариант є 16
“реугольник задаетс€ координатами своих вершин на плоскости:  ,
,  ,
,  . Ќайти внутренние углы треугольника ABC (в градусах).
. Ќайти внутренние углы треугольника ABC (в градусах).
|
|
|
¬ариант є 17
“реугольник задаетс€ координатами своих вершин на плоскости:  ,
,  ,
,  . Ќайти длину и основание высоты, опущенной из вершины A на сторону BC.
. Ќайти длину и основание высоты, опущенной из вершины A на сторону BC.
¬ариант є 18
“реугольник задаетс€ координатами своих вершин на плоскости: 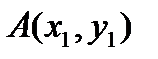 ,
,  ,
,  . Ќайти точку D, симметричную точке A относительно стороны BC.
. Ќайти точку D, симметричную точке A относительно стороны BC.
¬ариант є 19
¬ равнобедренном пр€моугольном треугольнике известна высота h, опущенна€ на гипотенузу. Ќайти стороны треугольника.
¬ариант є 20
Ђ осойї квадрат. ” квадрата ABCD на плоскости известны координаты двух противоположных вершин Ц точек A и C. Ќайти координаты точек B и D.
ѕримечание. –асположение квадрата произвольно, его стороны не об€зательно параллельны координатным ос€м.
¬ариант є 21
“реугольник ABC задан длинами своих сторон. Ќайти длину высоты, опущенной из вершины A.
¬ариант є 22
«аданы уравнени€ двух пересекающихс€ пр€мых на плоскости:  ,
,  . Ќайти (в градусах, минутах и секундах) угол между ними, использу€ формулу:
. Ќайти (в градусах, минутах и секундах) угол между ними, использу€ формулу:  .
.
¬ариант є 23
“рехмерные вектора заданы своими координатами, например,  ,
,  . Ќайти угол в градусах между векторами A и B, использу€ формулу:
. Ќайти угол в градусах между векторами A и B, использу€ формулу:  .
.
¬ариант є 24
“рехмерные вектора заданы своими координатами, например,  ,
,  ,
,  . Ќайти объем пирамиды, построенной на векторах A, B, C, как на сторонах.
. Ќайти объем пирамиды, построенной на векторах A, B, C, как на сторонах.
¬ариант є 25
“рехмерные вектора заданы своими координатами, например,  ,
,  ,
,  . Ќайти длину диагонали параллелепипеда, построенного на векторах A, B, C, как на сторонах.
. Ќайти длину диагонали параллелепипеда, построенного на векторах A, B, C, как на сторонах.
¬ариант є 26
ќпределить периметр правильного n-угольника, описанного около окружности радиуса r.
¬ариант є 27
»звестна длина окружности. Ќайти площадь круга, ограниченного этой окружностью.






