Кулоновские силы являются консервативными.
Каждый точечный заряд создает в пространстве силовое поле, которое можно изобразить с помощью направленных силовых линий, которые всегда начинаются на положительных зарядах и заканчиваются на отрицательных.
Это силовое поле действует с некоторой силой на каждый точечный заряд, помещенный в данную точку поля. Эта сила направлена по касательной к силовой линии поля. Точечный заряд, помещенный в поле, приобретает потенциальную энергию. Само поле обладает возможностью применить силу и совершить работу по перемещению помещенного в него точечного заряда. Электрическое поле имеет силовую и энергетическую характеристики.
Силовая характеристика электрического поля является векторной величиной и называется напряженностью. Вектор напряженности электрического поля определяется как сила, действующая на единицу электрического заряда, помещенного в данную точку поля:
Вектор напряженности, как и вектор силы, направлен по касательной к силовой линии поля.
Энергетическая характеристика электрического поля является скалярной величиной (числом) и называется потенциалом. Потенциал электрического поля определяется как потенциальная энергия (
) единицы электрического заряда, помещенного в данную точку поля:
В этом разделе для обозначения потенциальной энергии используется буква , так как буквой 
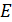обозначается напряженность поля.
Потенциал электрического поля измеряется в вольтах (В), а напряженность поля – в вольтах, деленных на метр.
Электрическое поле, созданное заряженными телами, является потенциальным. Здесь действует та же связь между консервативной силой и потенциальной энергией:
Разделив все члены уравнений на заряд 
, получим новые важные формулы:
Формула связи между напряженностью и потенциалом электрического поля в интегральном виде
Вектор напряженности электрического поля направлен в сторону уменьшения потенциала.
Электрическое поле, созданное зарядами, заставляет положительный заряд двигаться от большего потенциала к меньшему.
Разность потенциалов между двумя точками поля равна работе электрического поля по переносу единицы электрического заряда из первой точки поля во вторую.
Формула для расчета работы поля по перемещению точечного заряда
Работа электрического поля, созданного зарядами, по любой замкнутой траектории равна нулю (
). Циркуляция вектора напряженности этого электрического поля также равна нулю:
Электрическое поле, созданное зарядами, имеет потенциальный характер.
Если известны вектор напряженности и потенциал в каждой точке поля, то можно вычислить силу, действующую на любой точечный заряд
и потенциальную энергию точечного заряда
Можно получить формулу для вычисления модуля вектора напряженности электрического поля точечного заряда, применив закона Кулона, который справедлив именно для точечных зарядов, и формулу определения напряженности.
Формулу для вычисления потенциала электрического поля точечного заряда можно получить из формулы связи между напряженностью и потенциалом.
В обеих последних формулах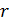 
– это расстояние от точечного заряда, создающего поле до заданной точки, в которой вычисляются модуль напряженности и потенциал.
Электрическое поле в любой точке пространства создается всеми имеющимися точечными зарядами, каждым из них независимо от других зарядов. Для вычисления вектора напряженности и потенциала используют принцип суперпозиции (суммирования):
Потенциальная энергия взаимодействия точечных зарядов вычисляется по формуле
Потенциальная энергия притяжения отрицательна (
), а потенциальная энергия отталкивания – положительна (
).
Электрический ток
Электрический ток – это направленное движение электрического заряда.
За направление тока принято направление движения положительного заряда.
Для характеристики тока используется физическая величина «сила тока», которая обозначается буквой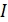 
и определяется как производная от заряда по времени
Cила тока измеряется в амперах (А). 
Магнитное взаимодействие
Электрический ток (в том числе и каждый движущийся заряд) создает в пространстве магнитное поле, которое действует на другой электрический ток (другой движущийся заряд) и наоборот.
Но магнитное поле имеет другую конфигурацию. Магнитное поле имеет вихревой характер. Его силовые линии не имеют ни начала, ни конца. Силовые линии магнитного поля замкнутые. Линии тока, создавшие магнитное поле, проходят внутри силовых линий магнитного поля перпендикулярно им. Направление магнитных силовых линий соответствует правилу правой руки.
ток
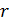
Силовая линия магнитного поля
Чем больше расстояние 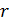от тока, тем магнитное поле слабее.
Магнитное поле имеет силовую характеристику, которую называют вектором магнитной индукции. Вектор магнитной индукции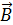 
направлен по касательной к силовой линии магнитного поля.
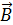
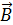
Циркуляция вектора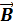 
по любому замкнутому контуру не равна нулю. Она пропорциональна силе тока, создавшего магнитное поле.
Отличие циркуляции силового вектора от нуля является признаком вихревого характера поля.
Магнитное поле действует только на проводник с электрическим током или на движущийся электрический заряд. Чем больше модуль вектора магнитной индукции, тем больше сила действия магнитного поля.
Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера.
Сила, с которой магнитное поле действует на движущийся электрический заряд, называется силой Лоренца.
Обе эти силы являются векторными произведениями. Их направление соответствует правилу правого буравчика.
Сила Ампера вычисляется по формуле
Модуль силы Ампера вычисляется по формуле
Максимальная сила со стороны магнитного поля действует на проводник с током, расположенный перпендикулярно магнитному полю.
Эта формула используется для определения величины магнитной индукции.
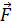
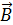
Магнитная индукция измеряется в теслах (Тл).
Сила Лоренца вычисляется по формуле
Сила Лоренца всегда направлена перпендикулярно к вектору скорости 
движущегося заряда , и сообщает электрическому заряду нормальное ускорение.
Модуль силы Лоренца равен
Максимальная сила Лоренца действует на заряд тогда, когда его скорость перпендикулярна вектору 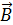. В этом случае заряд будет двигаться по окружности с радиусом 
.
Произведение массы заряда на нормальное ускорение и будет равно этой максимальной силе:
При этом период 
обращения заряда по окружности (время одного полного оборота) будет равен
Законы Ома
C торонние силы. Эдс.
Электрическое поле, созданное зарядами, способно вызвать направленное движение положительного заряда от большего потенциала к меньшему и не может создать электрический ток в замкнутой цепи.
Для создания и поддержания разности потенциалов нужны сторонние силы. Это любые силы неэлектрической природы, вызывающие перемещение зарядов. Сторонние силы, действуют внутри источника тока.
|
|
|
|
Эти сторонние силы перемещают положительный заряд от меньшего потенциала (
) к большему (). – вектор напряженности поля сторонних сил.
Условное обозначение источника тока на электрических схемах выглядит так.
Вектор напряженности сторонних сил направлен от минуса к плюсу источника тока.
Работа сторонних сил по переносу единицы электрического заряда называется эдс:
Эдс, как потенциал, измеряется в вольтах.
Закон Ома в локальной форме (для каждой точки проводника).
Электрический ток может идти в проводящих средах (проводниках), где есть «свободные» носители заряда. У каждого проводника имеется в каждом его малом объеме удельное сопротивление 
.
Пусть электрический ток идет по проводнику через поперечное сечение площади 
.
Вектор , направленный вдоль тока, называется вектором плотности тока.
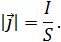
Вектор плотности тока прямо пропорционален величине суммарного вектора напряженностей электрического поля и поля сторонних сил и обратно пропорционален удельному сопротивлению – закон Ома в локальной форме.
Закон Ома для неоднородного участка.
Это участок электрической цепи, содержащий проводники и источники тока.
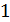
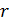
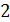
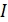
Проинтегрируем закон Ома в локальной форме по всему этому участку.
Рассмотрим каждый интеграл по отдельности.
Эта величина называется напряжением. Напряжение на участке цепи 1-2 равно произведению силы тока на сопротивление 
этого участка.
Напряжение, как потенциал, измеряется в вольтах. Сопротивление проводника измеряется в Омах. 
Первый интеграл справа – это разность потенциалов между точками 1 и 2.
Второй интеграл справа – это эдс.
Мы получили закон Ома для неоднородного участка цепи.
Напряжение на участке цепи 1-2 равно сумме разности потенциалов на концах участка и эдс на этом участке. Все величины в этом уравнении алгебраические. Их знаки определяются по направлению тока.
Напряжение – это полная работа по перемещению единицы заряда по участку цепи, равная сумме работ электрического поля и поля сторонних сил по перемещению единицы заряда.
Закон Ома для замкнутой цепи.
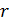
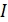
Пусть замкнутая цепь состоит и источника тока с эдс и внутренним сопротивлением 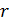и нагрузки с сопротивлением . Замкнутая цепь не имеет ни начала, ни конца, следовательно,
Сопротивление всей цепи равно сумме сопротивлений источника тока (внутренний участок) и сопротивления нагрузки (внешний участок).
Закон Ома для замкнутой цепи:
Напряжение на внешнем участке (нагрузке):
Это напряжение равно разности потенциалов на внешнем участке
Источник тока и нагрузка находятся между теми же двумя точками, делящими замкнутую цепь на внутренний участок и внешний участок. Следовательно, разность потенциалов на внутреннем участке по модулю равна напряжению на внешнем участке.
Напряжение на внутреннем участке (источнике тока):
