Движение и покой относительны. О движении какого-нибудь физического тела можно говорить лишь по отношению к другому телу – наблюдателю, с которым связывают систему отсчета –прямоугольную систему координат 
.
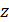
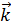
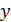
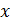
В этой системе отсчета вдоль каждой из осей 
отложены соответственно единичные векторы (орты) , и 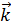. Каждая точка имеет координаты .
Если материальная точка находится в точке , то из начала координат в точку проводится радиус – вектор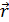 
.
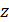
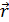
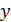
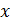
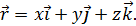
Координаты радиуса – вектора совпадают с координатами точки .
Модуль радиуса – вектора измеряется в метрах (м).
Пусть материальная точка переместилась из положения 1 в положение 2 по нарисованной траектории. Радиус – вектор изменился.
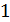
траектория
где вектор
называется перемещением.
Если промежуток времени 
между первым и вторым положениями тела стремится к нулю (
), то есть превращается в дифференциал 
, то и вектор перемещения превращается в дифференциал 
, который совпадает с бесконечно малым кусочком траектории 
:
Быстроту и направление перемещения показывает вектор скорости, который определяется как производная от радиуса – вектора по времени:
Вектор скорости совпадает по направлению с векторами 
, и поэтому вектор скорости всегда направлен по касательной к траектории.
Согласно последней формуле любое криволинейное движение можно представить в виде суммы трех прямолинейных движений по осям 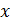, 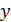и .
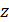Вектор скорости имеет модуль
и три проекции 
, 
и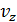 
. Модуль и проекции вектора скорости измеряются в метрах в секунду (м/с).
Путь 
, пройденный телом за некоторый промежуток времени
можно вычислить путем интегрирования
Средняя скорость тела на этом промежутке вычисляется по формуле
Вектор скорости может со временем изменяться по величине и по направлению. В этом случае движение происходит с ускорением.
Вектор ускорения определяется как производная от вектора скорости по времени:
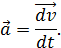
Модуль и проекции вектора ускорения измеряются в 
.
Если вектор ускорения направлен параллельно вектору скорости, то тело движется прямолинейно.
Если вектор ускорения направлен в сторону вектора скорости, то скорость по модулю возрастает.
Если вектор ускорения направлен в противоположную сторону, то скорость по модулю уменьшается.
В этом случае ускорение является тангенциальным. Тангенциальное ускорение 
отвечает только за модуль скорости и определяется по формуле
Если вектор ускорения направлен под углом к вектору скорости, то тело движется криволинейно.
Если вектор ускорения направлен перпендикулярно к вектору скорости, то тело движется равномерно по кривой траектории. В этом случае ускорение является нормальным.
Нормальное ускорение отвечает только за направление скорости и определяется по формуле
где 
– радиус кривизны траектории.
Если вектор ускорения составляет с вектором скорости острый или тупой угол, то у тела имеются и тангенциальное, и нормальное ускорения.
