Порядок работы с картой Карно

Лекция №11

Упрощение логических выражений методом карт Карно

План

1. Куб Карно.

2. Принцип минимизации.

3. Порядок работы с картой Карно.

 

Куб Карно

Куб Карно́ — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом

Принцип минимизации

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Аналогично для КНФ:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2 ^N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N –мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

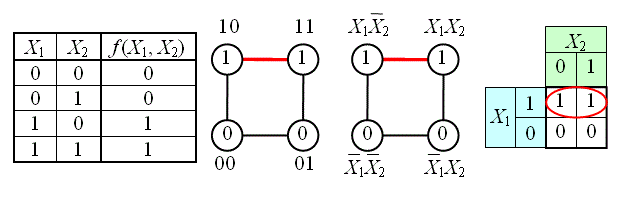
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Таблица не верна. Верной будет: 1 1 0 0 1 1 0 0. Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2 ^K термов, принадлежащие одной K –мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом, появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями пяти, семи (обязательно простое число) и т.д., используя не визуализируемые многомерные булевы кубы.

 

Порядок работы с картой Карно

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2 ^N наборах входных переменных X ₁... X_N. Карта Карно также содержит 2 ^N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X ₁... X_N. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

В данном разделе в качестве примера используется функция четырёх переменных, заданная таблицей истинности, изображённой на рис. 2а. Карта Карно для той же функции изображена на рис. 2б.

 

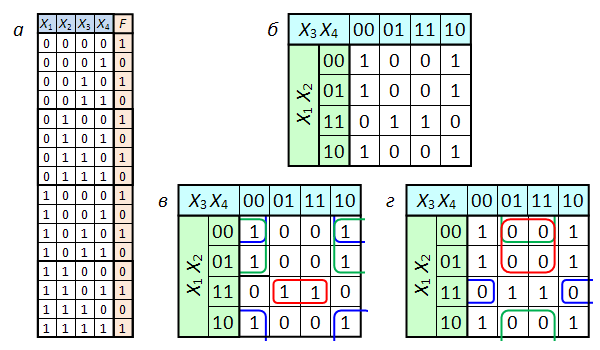
Рис. 2. Пример работы с картой Карно

Принципы склейки

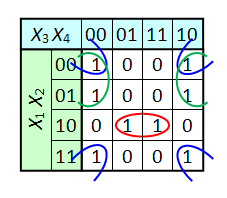
· Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить ДНФ) или по нулям (если требуется КНФ).

· Склеивать можно только прямоугольные области с числом единиц (нулей) 2 ⁿ, где n — целое число. Для карт Карно с числом переменных более четырёх могут получаться более сложные области, о чём будет сказано в следующих разделах.

· Область, которая подвергается склейке должна содержать только единицы (нули).

· Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N =4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат, как показано на рис. 2в.

· Все единицы (нули) должны попасть в какую-либо область.

· С точки зрения минимальности ДНФ (КНФ) число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм. Терм размером 2 ⁿ ячеек содержит N – n переменных).

· Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:

· В отличие от СДНФ (СКНФ), ДНФ (КНФ) не единственны. Возможно несколько эквивалентных друг другу ДНФ (КНФ), которые соответствуют разным способам покрытия карты Карно прямоугольными областями.

 

Описание

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути, Карта Карно — это таблица истинности, составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.е. вся Карта Карно сворачивается в фигуру тор (бублик) (рис.4.1).

Рис. 4.1. Метод скручивания карты Карно

На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала ( целое число = 0… ) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули;

2. Область должна располагаться симметрично оси (ей) (оси располагаются через каждые четыре клетки);

3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну;

4. Область должна быть как можно больше, а количество областей как можно меньше;

5. Области могут пересекаться;

6. Возможно несколько вариантов покрытия.

Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
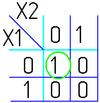
Например (для Карт на 2 переменные):

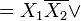
Для КНФ всё то же самое, только рассматриваем клетки с нулями, неменяющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:

В формате КНФ:

Так же из ДНФ в КНФ и обратно можно перейти использовав Законы де Моргана.

 

Примеры:

Пример 1.

Упростить полученную СДНФ, используя склеивание, а так же применить карту Карно для получения ДНФ.

, применено свойство и склеивание по «z» и по «y».

Дизъюнкции в скобках получены по парам наборов переменных (0,0,0), (0,0,1) и (0,0,0), (0,1,0). Наборы в каждой паре отличаются только в одной позиции и называются соседними. После упрощения остаются совпадающие в паре переменные. Карты Карно представляют собой таблицу истинности, в которой соседние наборы переменных расположены рядом (метод скользящей единицы при этом нарушается).

Для нашей функции имеем

yz x

Карты Карно позволяют получить ДНФ минимальную по числу переменных или их отрицаний. Для этого необходимо заключить в круги рядом стоящие значения функции равные 1, причём

1) Каждый руг может содержать только 2^K (к = 0, 1, 2,…) единиц, например16, 8, 4, 2, 1.

2) Круги должны быть наибольшего размера.

3) Число кругов наименьшее, покрывающее все единицы.

4) Так как наборы (0,0) и (1,0) соседние. То края карты соединяются друг с другом.

5) По каждому из кругов составляется простая конъюнкция, входящая в ДНФ. При этом оставляются только те переменные, которые сохраняют свое значение во всем круге и как обычно, если х_i = 1, то пишем х_i, если х_i = 0, то .

Построим круги для нашего примера.

yz x
		1 1		1 2

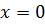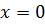Имеем две конъюнкции. Для первого круга и сохраняют свое значение, получаем . Во втором круге не меняется и , получаем . Окончательно .

 

Пример 2

У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу, если ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родственников единицей, несогласие - нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:

 

Перерисуем таблицу истинности в 2-х мерный вид:

Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:

Заполним её значениями из таблицы истинности:

Минимизируем в соответствии с правилами:

 

1. 1. Все области содержат 2^n клеток;

2. 2. Так как Карта Карно на четыре переменные, оси располагаются на границах Карты и их не видно (подробнее смотри пример Карты на 5 переменных);

3. 3. Так как Карта Карно на четыре переменные, все области симметрично осей — смежные между собой (подробнее смотри пример Карты на 5 переменных);

4. 4. Области S3, S4, S5, S6 максимально большие;

5. 5. Все области пересекаются (необязательное условие);

6. 6. В данном случае рациональный вариант только один.

Теперь по полученной минимальной ДНФ можно построить логическую схему:

Из-за отсутствия в наличии шести - входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы (D7, D8).

Составим мин. КНФ:

 

 

 

Заключение.

Для минимизации логических функций возможно использовать разные методы:

• карта Карно (Вейча)
• Квайна
• Квайна- Мак-Класки
• Петрика

Отличие метода карт Карно от карт Вейча заключается в способе обозначения строк и столбцов карт. У карт Карно строки и столбцы обозначаются с помощью кода Грея. Однако, принципиальной разницы между ними нет.

Метод минимизационных карт Карно (или карт Вейча) хорошо работает при числе аргументов 3,4 и даже 5 и обеспечивает простоту получения результата. Этот метод основан на зрительном анализе таблиц (карт) и не может быть применен для обработки вычислительной техникой.

 

 

Домашнее задание:

1. Минимизировать нижеприведённые функции, представленные картами Карно.

Не заполненные клетки соответствуют нулю. Переменные, обозначенные буквами, соответствуют прямому значению, а не обозначенные - инверсному.

 

 

Контрольные вопросы:

1. Определение куба Карно.

2. Кем и в каком году были изобретены карты Карно?

3. Основной метод минимизации логических функций?

4. Принципы склейки карты Карно.

5. В какую фигуру сворачивается карта Карно?