“ема: ќсновные параметры состо€ни€.
“ермические и калорические параметры состо€ни€
термическим параметрам состо€ни€ относ€тс€ давление P, удельный объем v,температура “.
калорическим параметрам состо€ни€ относ€тс€ следующие основные термодинамические величины: энтропи€ S, внутренн€€ энерги€ U и энтальпи€ H = U + PV
“ермодинамические параметры состо€ни€
—войства каждой системы характе≠ризуютс€ р€дом величин, которые при≠н€то называть термодинамиче≠скими параметрами. –ассмот≠рим некоторые из них, использу€ при этом известные из курса физики молекул€рно-кинетические представлени€ об идеальном газе как о совокупности моле≠кул, которые имеют исчезающе малые размеры, наход€тс€ в беспор€дочном тепловом движении и взаимодействуют друг с другом лишь при соударени€х.
ƒавление Ч физическа€ величина, численно равна€ отношению нормальной составл€ющей силы к площади, на которую действует эта сила.
≈диницей давлени€ в —» €вл€етс€ ѕаскаль Ч давление, вызываемое силой в 1 Ќ, равномерно распределенной по поверхности площадью 1 м2 (1ѕа=1 Ќ/м2).
¬ табл. 1.1 приведены соотношени€ между ранее примен€вшимис€ единицами измерени€ давлени€ и единицами давлени€ в —».
| “аблица 1.1 | ||||||
| ≈диница | ѕа | бар | кгс/см2 | мм рт.ст. | мм вод.ст. | |
| 1 ѕа | 10-5 | 1,02Ј10-5 | 7,5024Ј10-3 | 1,02Ј10-1 | ||
| 1 бар | 105 | 1,02 | 7,5024Ј102 | 1,02Ј104 | ||
| 1 кгс/см2 | 9,8067Ј104 | 0,98067 | 104 | |||
| 1 мм рт.ст. | 1,33Ј10-3 | 1,36Ј10-3 | 13,6 | |||
| 1 мм вод.ст. | 9,8067 | 9,8067Ј10-5 | 10-4 | 7,35Ј10-2 |
–азличают атмосферное, или барометрическое давление Pб, абсолютное давление –а, манометрическое –м, или избыточное –изб давление, разрежение, или вакуум.
ƒавление, создаваемое атмосферным воздухом, называетс€ барометрическим, или атмосферным.
јбсолютным давлением, называетс€ давление отсчитываемое от нул€ (абсолютного вакуума).
»збыточным, или манометрическим, давлением называетс€ давление сверх атмосферного, то есть избыточное давление Ч это разность между абсолютным и барометрическим давлени€ми: Pизб = Pa - Pб.
–азрежением, или вакуумом, называетс€ разность между атмосферным давлением и абсолютным давлением той среды, где измер€етс€ давление. ≈сли абсолютное давление газа или пара в сосуде ниже барометрического, то есть Pа < Pб, то разность Pв = Pa Ц Pб называетс€ разрежением, или вакуумом.
¬акуум показывает, насколько давление газа (пара) меньше давлени€ окружающей среды. ƒавление атмосферного воздуха измер€етс€ барометрами, избыточное давление Ч мано≠метрами, а давление разрежени€ Ч вакуумметрами.
¬ термодинамических уравнени€х всегда используют значени€ абсолютного давлени€ ввиду того, что оно €вл€етс€ параметром, характеризующим состо€ние термодинамической системы.
јтмосферное давление Ч величина переменна€, поэтому в технике примен€етс€ нормальное атмосферное давление, –б = 0,10132 ћ ѕ а (760 мм рт. ст.).
ƒавление обусловлено взаимо≠действием молекул рабочего тела с по≠верхностью и численно равно силе, дей≠ствующей на единицу площади повер≠хности тела по нормали к последней. ¬ соответствии с молекул€рно-кинетической теорией давление газа определ€етс€ соотношением
|
|
|
 , (1.1)
, (1.1)
где n Ч число молекул в единице объема;
т Ч масса молекулы; с2 Ч сред≠н€€ квадратическа€ скорость поступательного движени€ молекул.
¬ ћеждународной системе единиц (—») давление выражаетс€ в паскал€х (1 ѕа=1 Ќ/м2). ѕоскольку эта едини≠ца мала, удобнее использовать 1 кѕа = 1000 ѕа и 1 ћѕа=106 ѕа.
ƒавление измер€етс€ при помощи манометров, барометров и вакуумметров.


 ∆идкостные и пружинные манометры измер€ют избыточное давление, пред≠ставл€ющее собой разность между пол≠ным или абсолютным давлением р изме≠р€емой среды и атмосферным давлением p атм, т.е.
∆идкостные и пружинные манометры измер€ют избыточное давление, пред≠ставл€ющее собой разность между пол≠ным или абсолютным давлением р изме≠р€емой среды и атмосферным давлением p атм, т.е. 
ѕриборы дл€ измерени€ давлений ниже атмосферного называютс€ вакуум≠метрами; их показани€ дают значение разрежени€ (или вакуума):
 , т. е. избыток атмосферного давлени€ над абсолютным.
, т. е. избыток атмосферного давлени€ над абсолютным.
—ледует отметить, что параметром состо€ни€ €вл€етс€ абсолютное давле≠ние. »менно оно входит в термодинами≠ческие уравнени€.
“емпература тела есть мера его нагретости. “емпература определ€ет направление передачи теплоты. ≈сли два тела ј и ¬ имеют соответственно температуру “1 и “2 и “1>“2, то теплота переходит от тела ј к телу ¬. ѕри этом температура тела ј уменьшаетс€, а тела ¬ - увеличиваетс€.
— точки зрени€ молекул€рно-кинетической теории температура есть мера интенсивности теплового движени€ молекул.
¬ термодинамике рассматривают температуру как среднестатистическую величину, котора€ характеризует систему, состо€щую из очень большого числа молекул (частиц), наход€щихс€ в хаотическом (тепловом) движении. ѕоэтому к единичным молекулам пон€тие температуры не применимо. ѕри температуре абсолютного нул€ тепловое движение молекул отсутствует. Ёта предельна€ минимальна€ температура называетс€ абсолютным нулем и €вл€етс€ началом дл€ отсчета температур. ѕон€тно, что не может быть “< 0, то есть абсолютна€ температура всегда положительна.
“емпература, отсчитываема€ от абсолютного нул€, называетс€ абсолютной, а шкала температур называетс€ шкалой ельвина.
ѕрактически измер€ть кинетическую энергию молекул газа непосредственно невозможно. ѕоэтому дл€ измерени€ температуры используют различные косвенные методы. “емпература измер€етс€ при помощи различных термометрических устройств Ц (термометров).
»спользование термометров основано на том факте, что два соприкасающихс€ тела с разными температурами через некоторое врем€ приход€т к состо€нию теплового равновеси€ и принимают одинаковую температуру.
„исленный отсчет температуры производитс€ по шкале температур. «а основную единицу измерени€ температуры принимают градус, имеющий разную величину в различных температурных шкалах. Ўкала температур устанавливаетс€ путем делени€ разности показаний термометра в двух произвольно выбранных посто€нных температурных точках, называемых реперными или опорными, на некоторое число равных частей Ч градусов.
¬виду того, что выбор посто€нных температурных точек и цены делени€ шкалы €вл€етс€ произвольным, имеетс€ р€д различных шкал температуры.
¬ насто€щее врем€ кроме абсолютной температуры примен€ютс€ другие температурные шкалы, такие, например, как: ÷ельси€, ‘аренгейта, –еомюра, –анкина.
ѕо шкале ÷ельси€ ( ) прин€ты следующие посто€нные температурные точки: ќ∞C Ч температура та€ни€ льда, 100∞C Ч температура кипени€ воды при нормальном атмосферном давлении.
) прин€ты следующие посто€нные температурные точки: ќ∞C Ч температура та€ни€ льда, 100∞C Ч температура кипени€ воды при нормальном атмосферном давлении.
|
|
|
¬ 1724 г. ‘аренгейт предложил термометр, в качестве реперных точек которого прин€ты: +212∞F Ч температура кипени€ воды при нормальном атмосферном давлении; +32∞F - температура та€ни€ льда. –азность температур кипени€ воды и та€ни€ льда по шкале ‘аренгейта равна 212∞Ч 32∞ = 180 ∞F, а по шкале ÷ельси€ Ч 100∞C. —ледовательно, 1∞F соответствует 5/9 ∞C, а 1∞C Ч 1,8∞F.
Ўкала –еомюра ( ) имеет следующие реперные точки: ќ∞R Ч температура та€ни€ льда, 80∞R Ч температура кипени€ воды при нормальном атмосферном давлении.
) имеет следующие реперные точки: ќ∞R Ч температура та€ни€ льда, 80∞R Ч температура кипени€ воды при нормальном атмосферном давлении.
Ўкала –анкина ( ) Ч это шкала ‘аренгейта, отсчитанна€ от абсолютного нул€. ¬ этой шкале температура та€ни€ льда
) Ч это шкала ‘аренгейта, отсчитанна€ от абсолютного нул€. ¬ этой шкале температура та€ни€ льда  (T0=273,15 ) соответствует 491,67∞Ra, а температура кипени€ воды при нормальном атмосферном давлении (T0=373,15 ) соответствует 671,67∞Ra.
(T0=273,15 ) соответствует 491,67∞Ra, а температура кипени€ воды при нормальном атмосферном давлении (T0=373,15 ) соответствует 671,67∞Ra.
–ешением ћеждународного комитета мер и весов прин€ты две шкалы: термодинамическа€ температурна€ шкала, котора€ прин€та основной, и ћеждународна€ практическа€ температурна€ шкала (ћѕ“Ў-68), выбранна€ таким образом, чтобы температура, измеренна€ по этой шкале, была близка к термодинамической. ¬ основу построени€ термодинамической шкалы положен тот факт, что в циклах арно, располагающихс€ между двум€ адиабатами, разность температур изотерм считаетс€ посто€нной, если в механическую работу превращаютс€ одинаковые количества теплоты. Ќаиболее универсальной шкалой температур €вл€етс€ абсолютна€ термодинамическа€ шкала температур Ч шкала ельвина.
¬ шкале ельвина используетс€ единственна€ экспериментальна€ реперна€ точка Ч тройна€ точка химически чистой воды (в термодинамическом равновесии наход€тс€ три агрегатных состо€ни€; лед, жидка€ вода и пар). Ётому состо€нию соответствует температура 273,15 (0,01∞—). ¬торой посто€нной точкой €вл€етс€ абсолютный нуль температур (0 ). ельвин Ч единица измерени€ температуры по термодинамической температурной шкале, равна€ 1/273,15 части интервала от абсолютного нул€ температуры до температуры тройной точки воды.
ѕрактическим осуществлением термодинамической шкалы температур €вл€етс€ ћеждународна€ практическа€ температурна€ шкала. ¬ этой шкале используетс€ одиннадцать реперных точек. ¬ табл. 1.2 приведены значени€ основных реперных точек.
| “аблица 1.2 | ||
| –авновесное состо€ние | ћѕЎ“-68 | |
| T68 | t68 | |
| “очка кипени€ кислорода | 90,188 | -182,962 0C |
| “ройна€ точка воды | 273,16 | +0,01 0C |
| “очка кипени€ воды | 373,15 | +100,0 0C |
| “очка плавлени€ цинка | 692,73 | +419,58 0C |
| “очка плавлени€ серебра | 1235,08 | +961,93 0C |
| “очка плавлени€ золота | 1337,58 | +1064,43 0C |
| “емпературы кипени€ и плавлени€ даны при давлении 101325 ѕа |
“емпературой называетс€ фи≠зическа€ величина, характеризующа€ степень нагретости тела. ѕон€тие о тем≠пературе вытекает из следующего утвер≠ждени€: если две системы наход€тс€ в тепловом контакте, то в случае нера≠венства их температур они будут обмени≠ватьс€ теплотой друг с другом, если же их температуры равны, то теплообмена не будет.
— точки зрени€ молекул€рно-кинетических представлений температура есть мера интенсивности теплового движени€ молекул. ≈е численное значение св€зано с величиной средней кинетической энер≠гии молекул вещества:
 , (1.2)
, (1.2)
где k Ч посто€нна€ Ѕольцмана, равна€ 1,380662Х10ˉ23 ƒж/ . “емпература T, определенна€ таким образом, называет≠с€ абсолютной.
¬ системе —» единицей температуры €вл€етс€ кельвин ( ); на практике широ≠ко примен€етс€ градус ÷ельси€ (∞—). —о≠отношение между абсолютной “ и стогра≠дусной I температурами имеет вид
 .
.
¬ промышленных и лабораторных ус≠лови€х температуру измер€ют с по≠мощью жидкостных термометров, пиро≠метров, термопар и других приборов.
”дельный объем вещества ν Ч это объем, занимаемый единицей массы данного вещества.
ѕлотность вещества ρЧ величина, обратна€ удельному объему и определ€юща€ количество вещества, заключенное в единице объема.
|
|
|
≈диница плотности в —» Ч кг/м3, в системе —√— Ч г/см3. ѕлотность и удельный объем завис€т от температуры и давлени€, то есть от термодинамического состо€ни€ вещества. ќбычно в справочниках привод€тс€ их значени€ при нормальных физических услови€х. «а нормальные физические услови€ принимают давление, равное 101,325 кѕа (760 мм рт. ст.), и температуру, равную 0 ∞—.
оличество вещества. ≈диницей количества вещества в —» €вл€етс€ моль. роме мол€ примен€ют кратные и дольные части от мол€ (кмоль, ћмоль и др.). оличество вещества Ч это физическа€ величина, определ€ема€ числом структурных элементов (атомов, молекул, ионов, электронов). ћоль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержитс€ атомов в углероде-12 массой 0,012 кг.
ћол€рной массой вещества называют отношение массы вещества к его количеству:

|
где μ Ч мол€рна€ масса. ≈сли  выразить в кг,
выразить в кг,  Ч в мол€х, μ Ч выразитс€ в кг/моль.
Ч в мол€х, μ Ч выразитс€ в кг/моль.
”дельный объем v Ч это объем единицы массы вещества. ≈сли однородное тело массой ћ занимает объем v, то по определению
v = V/ћ.
¬ системе —» единица удельного объема 1 м3/кг. ћежду удельным объемом вещества и его плотность существует очевидное соотношение:

ƒл€ сравнени€ величин, характери≠зующих системы в одинаковых состо€ни≠€х, вводитс€ пон€тие Ђнормальные физи≠ческие услови€ї:
p =760 мм рт.ст.= 101,325 кѕа; T =273,15 K.
¬ разных отрасл€х техники и разных странах ввод€т свои, несколько отличные от приведенных Ђнормальные услови€ї, например, Ђтехническиеї (p = 735,6 мм рт.ст.= 98 кѕа, t =15˚C) или нормальные услови€ дл€ оценки производительности компрессоров (p =101,325 кѕа, t =20˚—) и т. д.
≈сли все термодинамические пара≠метры посто€нны во времени и одинако≠вы во всех точках системы, то такое состо€ние системы называетс€ равно≠весным.
≈сли между различными точками в системе существуют разности темпера≠тур, давлений и других параметров, то она €вл€етс€ неравновесной. ¬ такой системе под действием гради≠ентов параметров возникают потоки теп≠лоты, вещества и другие, стрем€щиес€ вернуть ее в состо€ние равновеси€. ќпыт показывает, что изолированна€ система с течением времени всегда приходит в со≠сто€ние равновеси€ и никогда самопро≠извольно выйти из него не может. ¬ классической термодинамике рассмат≠риваютс€ только равновесные системы.
”равнение состо€ни€
ƒл€ равновесной термодинамической системы существует функциональна€ св€зь между параметрами состо€ни€, ко≠тора€ называетс€ уравнением со≠сто€ни€. ќпыт показывает, что удель≠ный объем, температура и давление про≠стейших систем, которыми €вл€ютс€ газы, пары или жидкости, св€заны термическим уравнением состо≠€ни€ вида  .
.
”равнению состо€ни€ можно придать другую форму: 


Ёти уравнени€ показывают, что из трех основных параметров, определ€ю≠щих состо€ние системы, независимыми €вл€ютс€ два любых.
ƒл€ решени€ задач методами термо≠динамики совершенно необходимо знать уравнение состо€ни€. ќднако оно не мо≠жет быть получено в рамках термодина≠мики и должно быть найдено либо экспе≠риментально, либо методами статистиче≠ской физики. онкретный вид уравнени€ состо€ни€ зависит от индивидуальных свойств вещества.
”равнение состо€ни€ идеальных га≠зов
»з уравнений (1.1) и (1.2) следует, что  .
.
–ассмотрим 1 кг газа. ”читыва€, что в нем содержитс€ N молекул и, следова≠тельно,  , получим:
, получим: 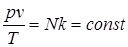 .
.
ѕосто€нную величину Nk, отнесен≠ную к 1 кг газа, обозначают буквой R и называют газовой посто€н≠ной. ѕоэтому
 , или
, или  . (1.3)
. (1.3)
ѕолученное соотношение представл€ет собой уравнение лапейрона.
”множив (1.3) на ћ, получим урав≠нение состо€ни€ дл€ произвольной массы газа ћ: 
|
|
|
 . (1.4)
. (1.4)
”равнению лапейрона можно при≠дать универсальную форму, если отнести газовую посто€нную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молеку≠л€рной массе μ. ѕоложив в (1.4) ћ= μ и V=V μ, получим дл€ одного мол€ урав≠нение лапейрона Ч ћенделеева:
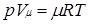 .
.
«десь  Ч объем киломол€ газа, а
Ч объем киломол€ газа, а  Ч универсальна€ газова€ посто€нна€.
Ч универсальна€ газова€ посто€нна€.
¬ соответствии с законом јвогадро (1811г.) объем 1 кмол€, одинаковый в одних и тех же услови€х дл€ всех иде≠альных газов, при нормальных физических услови€х равен 22,4136 м3, поэтому

√азова€ посто€нна€ 1 кг газа составл€ет  .
.
”равнение состо€ни€ реальных га≠зов
¬ реальных газах в отличие от иде≠альных существенны силы межмолеку≠л€рных взаимодействий (силы прит€же≠ни€, когда молекулы наход€тс€ на значи≠тельном рассто€нии, и силы отталкивани€ при достаточном сближении их друг с другом) и нельз€ пренебречь собствен≠ным объемом молекул.
Ќаличие межмолекул€рных сил от≠талкивани€ приводит к тому, что молеку≠лы могут сближатьс€ между собой толь≠ко до некоторого минимального рассто€≠ни€. ѕоэтому можно считать, что свобод≠ный дл€ движени€ молекул объем будет равен  , где b Ч тот наименьший объем, до которого можно сжать газ. ¬ соответствии с этим длина свободного пробега молекул уменьшаетс€ и число ударов о стенку в единицу времени, а следовательно, и давление увеличива≠етс€ по сравнению с идеальным газом в отношении
, где b Ч тот наименьший объем, до которого можно сжать газ. ¬ соответствии с этим длина свободного пробега молекул уменьшаетс€ и число ударов о стенку в единицу времени, а следовательно, и давление увеличива≠етс€ по сравнению с идеальным газом в отношении 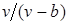 , т. е.
, т. е.
 .
.
—илы прит€жени€ действуют в том же направлении, что и внешнее давле≠ние, и привод€т к возникновению молеку≠л€рного (или внутреннего) давлени€. —ила молекул€рного прит€жени€ каких-либо двух малых частей газа пропорцио≠нальна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекул€рное давле≠ние обратно пропорционально квадрату удельного объема газа: рмол = а/ v 2, где а Ч коэффициент пропорциональности, завис€щий от природы газа.
ќтсюда получаем уравнение ¬ан-дер-¬аальса (1873 г.):
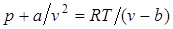 ,
,

 или
или
 .
.
ѕри больших удельных объемах и сравнительно невысоких давлени€х ре≠ального газа уравнение ¬ан-дер-¬аальса практически вырождаетс€ в уравнение состо€ни€ идеального газа лапейрона, ибо величина a / v 2
(по сравнению с p) и b (по сравнению с v) станов€тс€ прене≠брежимо малыми.
”равнение ¬ан-дер-¬аальса с ка≠чественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всег≠да согласуютс€ с экспериментальными данными. ¬ р€де случаев эти отклонени€ объ€сн€ютс€ склонностью молекул ре≠ального газа к ассоциации в отдельные группы, состо€щие из двух, трех и более молекул. јссоциаци€ происходит вслед≠ствие несимметричности внешнего элек≠трического пол€ молекул. ќбразовавши≠ес€ комплексы ведут себ€ как самосто€≠тельные нестабильные частицы. ѕри столкновени€х они распадаютс€, затем вновь объедин€ютс€ уже с другими мо≠лекулами и т. д. ѕо мере повышени€ тем≠пературы концентраци€ комплексов с большим числом молекул быстро уменьшаетс€, а дол€ одиночных молекул растет. Ѕольшую склонность к ассоциа≠ции про€вл€ют пол€рные молекулы во≠д€ного пара.
“ермодинамический процесс
»зменение состо€ни€ термодинами≠ческой системы во времени называетс€ термодинамическим процессом. “ак, при перемещении поршн€ в цилиндре объЄм, а с ним давление и температура наход€щегос€ внутри газа будут измен€тьс€, будет совершатьс€ процесс расширени€ или сжати€ газа.
ак уже отмечалось, система, выве≠денна€ из состо€ни€ равновеси€, и пре≠доставленна€ при посто€нных парамет≠рах окружающей среды самой себе, че≠рез некоторое врем€ вновь придет в рав≠новесное состо€ние, соответствующее этим параметрам. “акое самопроизволь≠ное (без внешнего воздействи€) возвра≠щение системы в состо€ние равновеси€
называетс€ релаксацией, а промежуток времени, в течение которого система возвращаетс€ в состо€ние равновеси€, называетс€ временем релаксации. ƒл€ разных процессов он различно: если дл€ установлени€ равновесного давлени€ в газе требуетс€ всегда, то дл€ выравнивани€ температуры в объеме того же газа нужны дес€ти; минут, а в объеме нагреваемого твердой тела Ч иногда несколько часов.
“ермодинамический процесс называетс€ равновесным, если все пара≠метры системы при его протекании мен€≠ютс€ достаточно медленно по сравнению с соответствующим процессом релакса≠ции. ¬ этом случае система фактически все врем€ находитс€ в состо€нии равно≠веси€ с окружающей средой, чем и опре≠дел€етс€ название процесса.
„тобы процесс был равновесным, скорость изменени€ параметров систе≠мы  должна удовлетвор€ть соотно≠шению
должна удовлетвор€ть соотно≠шению

где ј Ч параметр, наиболее быстро из≠мен€ющийс€ в рассматриваемом процес≠се; с рел Ч скорость изменени€ этого па≠раметра в релаксационном процессе; τ рел Ч врем€ релаксации.
|
|
|
–ассмотрим, например, процесс сжа≠ти€ газа в цилиндре. ≈сли врем€ смеще≠ни€ поршн€ от одного положени€ до дру≠гого существенно превышает врем€ ре≠лаксации, то в процессе перемещени€ поршн€ давление и температура успеют выровн€тьс€ по всему объему цилиндра.
Ёто выравнивание обеспечиваетс€ непре≠рывным столкновением молекул, в ре≠зультате чего подводима€ от поршн€ к газу энерги€ достаточно быстро и рав≠номерно распредел€етс€ между ними. ≈сли последующие смещени€ поршн€ бу≠дут происходить аналогичным образом, то состо€ние системы в каждый момент времени будет практически равновесным. “аким образом, равновесный процесс состоит из непрерывного р€да последо≠вательных состо€ний равновеси€, поэто≠му в каждой его точке состо€ние термо≠динамической системы можно описать уравнением состо€ни€ данного рабочего тела. »менно поэтому классическа€ термодинамика в своих исследовани€х оперирует только равновесными процес≠сами. ќни €вл€ютс€ удобной идеализа≠цией реальных процессов, позвол€ющей во многих случа€х существенно уп≠ростить решение задачи. “ака€ идеали≠заци€ вполне обоснована, так как условие (1.8) выполн€етс€ на практике до≠статочно часто. ѕоскольку механические возмущени€ распростран€ютс€ в газах со скоростью звука, процесс сжати€ газа и цилиндре будет равновесным, если ско≠рость перемещени€ поршн€ много мень≠ше скорости звука.
ѕроцессы, не удовлетвор€ющие усло≠вию  , протекают с нарушени≠ем равновеси€, т. е. €вл€ютс€ неравновесными. ≈сли, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреватьс€ через его стенки, релаксиру€ к состо€нию равновеси€, соответ≠ствующему новым параметрам окружаю≠щей среды. ¬ процессе релаксации газ не находитс€ в равновесии с окружаю≠щей средой и его нельз€ характеризовать уравнением состо€ни€ хот€ бы потому, что в разных точках объема газа темпе≠ратура имеет различные значени€.
, протекают с нарушени≠ем равновеси€, т. е. €вл€ютс€ неравновесными. ≈сли, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреватьс€ через его стенки, релаксиру€ к состо€нию равновеси€, соответ≠ствующему новым параметрам окружаю≠щей среды. ¬ процессе релаксации газ не находитс€ в равновесии с окружаю≠щей средой и его нельз€ характеризовать уравнением состо€ни€ хот€ бы потому, что в разных точках объема газа темпе≠ратура имеет различные значени€.
«аконы идеальных газов
«акон Ѕойл€-ћариота
Ѕойль в 1662 году и ћариот в 1676 году обнаружили, что при 
 .
.
«акон √ей-Ћюссака
√ей-Ћюссак в 1802 году опытным путЄм установил, что при  , v / T = const.
, v / T = const.
«акон јвогадро
¬ 1811 году јвогадро выдвинул гипотезу: одинаковые объЄмы различных газов при одинаковых физических услови€х содержат одинаковые количества молекул. Ёта гипотеза, став после еЄ доказательства законом, приводит к одному важному следствию, согласно которому при одинаковых физических услови€х дл€ любых газов произведение молекул€рной массы газа на его удельный объЄм есть величина посто€нна€, т. е.  .
.
Ќапомним, что молекул€рной массой называетс€ количество вещества в граммах, численно равное его молекул€рной массе. Ќапример, молекул€рна€ масса углерода равна 12 граммам, а кислорода - 32 граммам.
ѕроизведение  представл€ет собой объЄм одного мол€ газа, который при нормальных физических услови€х равен 22,4 м3.
представл€ет собой объЄм одного мол€ газа, который при нормальных физических услови€х равен 22,4 м3.
ќтметим, что нормальным физическим услови€м соответствуют 760 мм рт. ст. и 00—, а нормальным техническим услови€м - 735 мм рт. ст. и 100—.
”равнение состо€ни€
—опоставление законов Ѕойл€-ћариота и √ей-Ћюссака привод€т к обобщЄнному закону Ѕойл€-√ей-Ћюссака:
 , ,
|
где R - характеристическа€ посто€нна€ идеального газа (при нормальных физических услови€х 
 , где
, где  - плотность при нормальных физических услови€х).
- плотность при нормальных физических услови€х).
Ёто уравнение, полученное лапейроном в 1834 году, называетс€ уравнением состо€ни€ идеальных газов или уравнением лапейрона.






