Магнитные моменты ядер измеряются в ядерных магнетонах. Ядерный магнетон
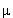 N = e N = e 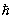 /2mpc, /2mpc,
|
где mp - масса протона.
Магнитный дипольный момент системы нуклонов 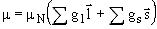 , где
, где 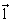 - орбитальный момент нуклона,
- орбитальный момент нуклона,  - его спин, а сумма берется по всем нуклонам системы. Безразмерные константы gl и gs называются соответственно орбитальным и спиновым гиромагнитными отношениями.
- его спин, а сумма берется по всем нуклонам системы. Безразмерные константы gl и gs называются соответственно орбитальным и спиновым гиромагнитными отношениями.
| Протон | Нейтрон | |
| gl | +1 | |
| gs | +5.586 | -3.826 |
Состояние дейтрона с j = 1 может быть представлено суперпозицией S1 и D1 состояний с относительными орбитальными моментами L = 0 и L = 2. В случае L = 0 спины протона и нейтрона параллельны, а в случае L = 2 их векторы направлены противоположно вектору орбитального момента. В этом последнем случае орбитальный момент каждого нуклона l = L/2 = 1 (см. рисунок).
Случай L = 0 (ln = lp = 0):  = =  N(1 N(1  0 + 0 0 + 0  0 + 5.586 0 + 5.586 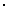 1/2 - 3.862 1/2 - 3.862 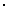 1/2) = 0,88 mN . 1/2) = 0,88 mN .
| 
|
Случай L = 2 (ln = lp = 1): 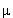 = = 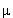 N(1 N(1 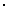 1 + 0 1 + 0 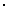 1 – 5.586 1 – 5.586 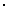 1/2 + 3.862 1/2 + 3.862 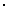 1/2) = 0,12 1/2) = 0,12 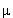 N. N.
| 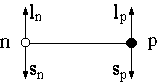
|
Обозначим вклад состояния с L = 2 как X. Тогда X 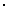 0,12
0,12 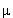 N + (1 – X)
N + (1 – X) 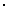 0,88
0,88 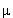 N = 0,86
N = 0,86 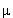 N. Получаем X = 0.026. То есть вклад состояния с L = 2 в волновую функцию дейтрона составляет 2,6%.
N. Получаем X = 0.026. То есть вклад состояния с L = 2 в волновую функцию дейтрона составляет 2,6%.
3. Известно, что внутренний электрический квадрупольный момент Q0 ядра 175Lu равен +5.9 Фм2. Какую форму имеет это ядро? Чему равен параметр деформации этого ядра?
Для равномерно заряженного аксиально симметричного эллипсоида, имеющего заряд Ze Q0 = 2Z(b2 - a2)/5, где b - полуось эллипсоида, направленная по оси симметрии Z, a a - по осям X и Y. Параметр деформации ядра
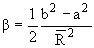 , ,
|
где 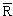 = (b + a)/2 - средний радиус ядра. Тогда
= (b + a)/2 - средний радиус ядра. Тогда
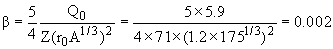 . .
|
Здесь учтено, что при малых деформациях 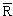
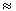 R = r0A1/3. Так как Q0 > 0, то b > a, и ядро представляет из себя эллипсоид вытянутый вдоль оси симметрии Z.
R = r0A1/3. Так как Q0 > 0, то b > a, и ядро представляет из себя эллипсоид вытянутый вдоль оси симметрии Z.
4. Внешний наблюдаемый квадрупольный момент ядра 85Rb Q = 0.7 б. Определить собственный квадрупольный момент ядра Q0, если спин ядра 85Rb равен J = 5/2.
Внешний наблюдаемый электрический квадрупольный момент ядра в лабораторной системе координат Q связан с собственным квадрупольным моментом ядра Q0 соотношением
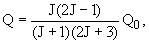
где J - спин ядра. Отсюда

5. Определить значения изоспинов I основных состояний ядер изотопов углерода 10C, 11C, 12C, 13C, 14C.
В основном состоянии ядра значение изоспина I совпадает с модулем проекции изоспина I = | Iz |. Проекция изоспина Iz ядра, состоящего из Z протонов и N нейтронов, равна
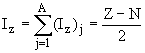 . .
|
То есть для основных состояний ядер I = |Z - N|/2.
Для указанных ядер значение изоспина будет:
для 10C - I = (6 – 4)/2 = 1,
для 11C - I = (6 – 5)/2 = 1/2,
для 12C - I = (6 – 6)/2 = 0,
для 13C - I = (7 – 6)/2 = 1/2,
для 14C - I = (8 – 6)/2 = 1.
6. Рассчитать расстояние между уровнями 1s, 2s и 3s ядра 90Zr для прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора.
В прямоугольной яме энергии уровней с l = 0 определяются соотношением:
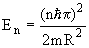 , ,
|
где n - главное квантовое число, m - масса нуклона и R - радиус ядра (ширина ямы). Величина расстояний между уровнями 1s, 2s и 3s будет
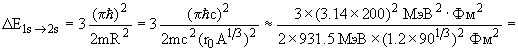
= 3 x 7.3 МэВ = 22 МэВ
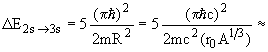
5 x 7.3 МэВ = 36.5 МэВ
В яме гармонического осциллятора выражение для энергии уровней с l = 0 определяется соотношением
En = 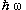 (2n + 3/2), где
(2n + 3/2), где 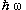 = 41 A1/3 = 41 x 901/3 = 9.1 МэВ для 90Zr.
= 41 A1/3 = 41 x 901/3 = 9.1 МэВ для 90Zr.
Расстояние будет 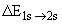 =
=  = 2
= 2 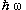 = 18.2 МэВ.
= 18.2 МэВ.
7. На основании одночастичной модели оболочек определить значения спинов и четностей J P основных состояний изотопов кислорода - 15O, 16O, 17O, 18O.
Изотопы 16O и 18O четно-четные, то есть имеют в основном состоянии спин и четность JP = 0+. Спин и четность ядра 15O определяются "нейтронной дыркой" (по отношению к четно-четному ядру 16O) в состоянии 1p1/2. Спин ядра J равен полному моменту "нейтронной дырки" в этом состоянии J = 1/2, а четность определяется орбитальным моментом l нуклона в данном состоянии P = (-1)l = (-1)1 = -1, то есть JP = 1/2-. Спин и четность ядра 17O определяется одним нейтроном в состоянии 1d5/2 сверх четно-четного остова ядра 16O. Для ядра 17O JP = 5/2+.
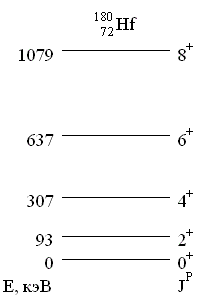
|
8. Показать, что спектр возбужденных состояний деформированного ядра 180Hf представляет собой "вращательную полосу".
Для четно-четных деформированных ядер энергия вращательных состояний
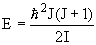 ,
,
где J - спин состояния, который принимает лишь четные значения J = 0, 2, 4, …, I - момент инерции ядра. Отношение энергий уровней должно быть следующим:
E2: E4: E6: E8 = J2(J2 + 1): J4(J4 + 1): J6(J6 + 1): J8(J8 + 1) = = 2(2 + 1): 4 (4 + 1): 6(6 + 1): 8 (8 + 1) = 3: 10: 21: 36.
Подставим приведенные на рисунке значения энергий и получим:
E2: E4: E6: E8 = 93: 307: 637:1079 = 93/31: 307/31: 637/31: 1079/31 = 3: 9.90: 20.55: 34.81.
Полученные отношения, а также отсутствие в спектре в спектре уровней с J = 1, 3, 5, … указывают, что это "вращательная полоса" ядра.
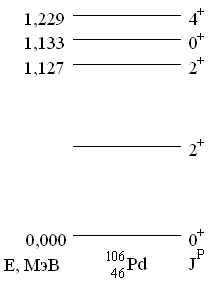
|
9. На схеме показан спектр возбужденных состояний ядра 106Pd. Оценить энергию первого возбужденного состояния 2+.
Это типичный спектр квадрупольных колебаний сферически симметричного ядра, имеющего в основном состоянии JP = 0+. Квадрупольные колебания атомных ядер характеризуются фононом JP = 2+. Положение энергетических уровней определяется числом фононов N: EN = (N + 5/2) 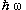 , где
, где 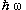 - энергия квадрупольного фонона. На рисунке есть только два уровня с JP = 2+, нижний (искомый) уровень имеет N = 1, а второй N = 2.
- энергия квадрупольного фонона. На рисунке есть только два уровня с JP = 2+, нижний (искомый) уровень имеет N = 1, а второй N = 2.
Тогда E0 = 5/2 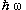 , E1 = 7/2
, E1 = 7/2 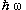 , E2 = 9/2
, E2 = 9/2 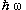 .
.
Энергия второго 2+ - состояния
E2 - E0 = (9/2 - 5/2) 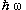 = 2
= 2 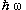 =1.127 МэВ.
=1.127 МэВ.
Энергия первого (искомого) 2+-состояния
E1 - E0 = (7/2 - 5/2) 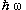 =
= 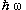 = 0.564 МэВ.
= 0.564 МэВ.
Для спектра квадрупольных колебаний четно-четных ядер имеющих в основном состоянии характерными особенностями являются следующие:
- Первое возбужденноое состояние имеет JP = 2+.
- При энергиях возбуждения, вдвое превышающих энергию первого возбужденного состояния должны находятся три состояния с примерно одинаковой энергией и имеющих квантовые характеристики JP = 0+, 2+, 4+, что соответствует сумме двух квадрупольных фононов 2+.
Радиоактивный распад
1. Активность препарата 32P равна 2 мкКи. Сколько весит такой препарат?
Закон радиоактивного распада:
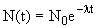 ,
,
где N0 - количество радиоактивных ядер в произвольно выбранный начальный момент времени t = 0, N(t) - количество радиоактивных ядер, не распавшихся к моменту времени t, 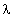 - постоянная распада (вероятность распада в единицу времени).
- постоянная распада (вероятность распада в единицу времени). 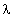 N - активность (интенсивность излучения) радиоактивного препарата, измеряется в Ки, 1 Ки = 3.7
N - активность (интенсивность излучения) радиоактивного препарата, измеряется в Ки, 1 Ки = 3.7 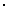 1010 распадов/с. T1/2 - период полураспада данного ядра (время, в течение которого количество радиоактивных ядер уменьшается в два раза) равен для 32P 14.5 суток. Период полураспада T1/2 связан с постоянной распада
1010 распадов/с. T1/2 - период полураспада данного ядра (время, в течение которого количество радиоактивных ядер уменьшается в два раза) равен для 32P 14.5 суток. Период полураспада T1/2 связан с постоянной распада 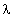 соотношением T1/2 = ln 2/
соотношением T1/2 = ln 2/ 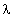 .
.
Количество ядер в образце массой m грамм

где NA - число Авогадро, A - массовое число. Активность препарата
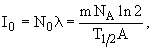
тогда его масса будет
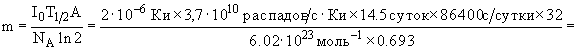
= 7.1 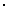 10-12 г.
10-12 г.
2. Во сколько раз число распадов ядер радиоактивного иода 131I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа 131I равен 193 часам.
Из закона радиоактивного распада N(t) = N0 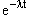 следует, что в течение первых суток (первых 24 часов) распалось
следует, что в течение первых суток (первых 24 часов) распалось 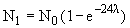 ядер.
ядер.
В течение вторых суток распалось 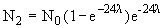 ядер.
ядер.
Отношение числа распадов за первые сутки к числу распадов за вторые сутки 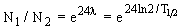 , где T1/2- период полураспада 131I в часах, связанный с
, где T1/2- период полураспада 131I в часах, связанный с 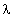 соотношением T1/2 = ln2/
соотношением T1/2 = ln2/ 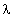 = 0.693/
= 0.693/ 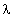 .
.
Окончательно 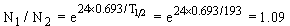 .
.
3. Определить энергию W, выделяемую 1 мг препарата 210Po за время, равное среднему времени жизни, если при одном акте распада выделяется энергия E = 5.4 МэВ.
Количество ядер радиоактивного препарата за среднее время жизни уменьшается в e = 2.718 раз. Тогда количество распавшихся за это время ядер будет D = 1 - 1/2.718 = 0.632 от их первоначального числа. Начальное число ядер Nв образце массой m грамм определяется из соотношения N = mNA/A, где NA - число Авогадро, A - массовое число. Количество энергии, выделившейся за время, равное среднему времени жизни изотопа 210Po
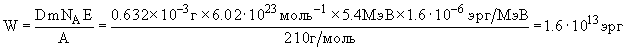 .
.
4. Определить верхнюю границу возраста Земли, считая, что весь имеющийся на Земле 40Ar образовался из 40K в результате e-захвата. В настоящее время на каждые 300 атомов 40Ar приходится один атом 40K.
Число нераспавшихся к настоящему времени ядер 40K
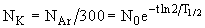 ,
,
где N0 - начальное число ядер 40K в момент образования Земли, t - возраст Земли. T1/2 - период полураспада 40K, составляющий 1.277 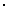 109 лет. При радиоактивном распаде 40K путем e- захвата распадается только 10.67% ядер, поэтому число ядер аргона к настоящему времени будет
109 лет. При радиоактивном распаде 40K путем e- захвата распадается только 10.67% ядер, поэтому число ядер аргона к настоящему времени будет
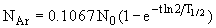 .
.
Получаем уравнение:
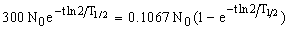 ,
,
откуда
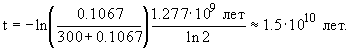
5. В результате  -распада радий 226Ra превращается в радон 222Rn. Какой объем радона при нормальных условиях будет находиться в равновесии с 1 г радия? Период полураспада 226Ra T1/2(Ra) = 1600 лет, 222Rn - T1/2(Rn) = 3.82 дня.
-распада радий 226Ra превращается в радон 222Rn. Какой объем радона при нормальных условиях будет находиться в равновесии с 1 г радия? Период полураспада 226Ra T1/2(Ra) = 1600 лет, 222Rn - T1/2(Rn) = 3.82 дня.
При установлении векового равновесия количество радиоактивных ядер обоих изотопов и их постоянные распада связаны уравнением
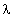 1N1 =
1N1 = 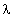 2N2,
2N2,
откуда
NRn = NRa 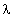 Ra/
Ra/ 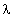 Rn = NRaT1/2(Rn)/T1/2(Ra).
Rn = NRaT1/2(Rn)/T1/2(Ra).
Количество ядер 226Ra
NRa = m NA/A,
где m и A- масса и массовое число 226Ra, NA - число Авогадро. Искомый объем
V = VMNRn/NA,
где VM - молярный объем газа (22.4 л/моль). Получаем
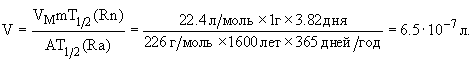
6. Определить сечение  реакции 31P(n,p)31Si, если известно, что после облучения мишени 31P толщиной d = 1 г/см2 в потоке нейтронов J = 2
реакции 31P(n,p)31Si, если известно, что после облучения мишени 31P толщиной d = 1 г/см2 в потоке нейтронов J = 2 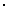 1010 с-1
1010 с-1 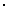 см-2 в течение времени tобл = 4 ч ее
см-2 в течение времени tобл = 4 ч ее 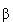 -активность I, измеренная через время tохл = 1 час после окончания облучения, оказалась I(tохл) = 3.9
-активность I, измеренная через время tохл = 1 час после окончания облучения, оказалась I(tохл) = 3.9 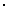 106 распадов/с. Период полураспада T1/2(31Si) = 157.3 мин.
106 распадов/с. Период полураспада T1/2(31Si) = 157.3 мин.
Число ядер 31Si, образующихся в 1 с в данной реакции
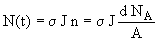 ,
,
где n - число ядер на единицу площади мишени, NA - число Авогадро, A- массовое число 31Si. Число распадающихся в 1 с ядер 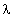 N(t), где
N(t), где 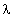 = ln 2/T1/2 = 60 х 0.693/157.3 = 0.264 ч-1 - постоянная распада 31Si. Тогда
= ln 2/T1/2 = 60 х 0.693/157.3 = 0.264 ч-1 - постоянная распада 31Si. Тогда
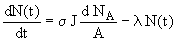 ,
,
при этом N(0) = 0. Получаем, что к моменту времени tобл образовалось ядер 31Si
 .
.
Через промежуток времени tохл после окончания облучения число ядер 31Si
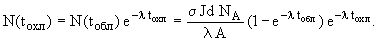
Активность препарата
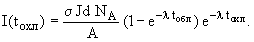
Для сечения реакции получаем
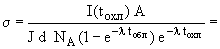
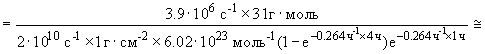
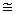 2
2 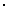 10-26 см2 = 20 мб.
10-26 см2 = 20 мб.
 7. Определить кинетические энергии
7. Определить кинетические энергии  -частиц
-частиц  , образующихся при
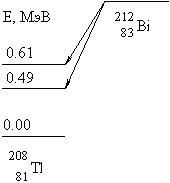
, образующихся при  - распаде 212Bi на возбужденные состояния ядра 208Tl с энергиями 0,49 и 0,61 МэВ. Энергия связи E св.(A,Z) ядра 212Bi - 1654.32 МэВ, ядра 208Tl - 1632.23 МэВ и
- распаде 212Bi на возбужденные состояния ядра 208Tl с энергиями 0,49 и 0,61 МэВ. Энергия связи E св.(A,Z) ядра 212Bi - 1654.32 МэВ, ядра 208Tl - 1632.23 МэВ и  -частицы - 28.30 МэВ.
-частицы - 28.30 МэВ.
Энергия a -распада из основного состояния исходного ядра в основное состояние конечного ядра Q0 определяется из соотношения
Q0 = (M(A,Z) - M(A- 4,Z- 2) - M(a))с2 = Eсв(A- 4,Z- 2) + Eсв(a) - Eсв(A,Z),
где M(A,Z) - масса исходного ядра, M(A - 4, Z - 2) - масса конечного ядра, M(a) - масса  - частицы и Eсв(A,Z), Eсв.(A- 4,Z- 2), Eсв(a) соответственно их энергии связи. В общем случае, когда распад происходит из возбужденного состояния начального ядра в возбужденное состояние конечного ядра, энергия
- частицы и Eсв(A,Z), Eсв.(A- 4,Z- 2), Eсв(a) соответственно их энергии связи. В общем случае, когда распад происходит из возбужденного состояния начального ядра в возбужденное состояние конечного ядра, энергия  - распада определяется соотношением
- распада определяется соотношением
Q = Q0 + Ei - Ef,
где Ei и Ef - энергии возбуждения начального и конечного ядер.
Кинетическая энергия a -частиц с учетом энергии отдачи конечного ядра
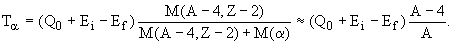
При распаде на первое возбужденное состояние (0.49 МэВ) ядра 208Tl
 = (1632.23 + 28.30 - 1654.32 - 0.49) МэВ х 208 а.е.м./212 а.е.м. = 5.61 МэВ.
= (1632.23 + 28.30 - 1654.32 - 0.49) МэВ х 208 а.е.м./212 а.е.м. = 5.61 МэВ.
При распаде на второе возбужденное состояние (0.61 МэВ) энергия  -частиц будет
-частиц будет
 = (1632.23 + 28.30 - 1654.32 - 0.61) МэВ х 208 а.е.м./212 а.е.м. = 5.49 МэВ.
= (1632.23 + 28.30 - 1654.32 - 0.61) МэВ х 208 а.е.м./212 а.е.м. = 5.49 МэВ.
8. Определить орбитальный момент l, уносимый  -частицей в следующих распадах:
-частицей в следующих распадах:

Для распада A 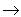 B + b запишем законы сохранения момента и четности
B + b запишем законы сохранения момента и четности
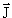 A = A = 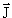 B + B +  b + b + 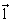 , ,
|
где 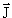 A,
A, 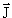 B,
B,  b - спины частиц A, B и b соответственно,
b - спины частиц A, B и b соответственно, 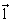 - орбитальный момент частицы b.
- орбитальный момент частицы b.
| PA = PBPb(-1)l |
где PA, PB, Pb - внутренние четности частиц A, B и b соответственно. Спин  -частицы 0, четность положительная. Законы сохранения момента и четности для
-частицы 0, четность положительная. Законы сохранения момента и четности для  -распада можно записать в виде
-распада можно записать в виде
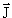 i = i = 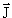 f + f + 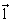 или |Ji - Jf| < l < Ji + Jf, или |Ji - Jf| < l < Ji + Jf,
|
где 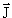 i,
i, 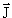 f - начального и конечного ядер.
f - начального и конечного ядер.
| Pi = Pf(-1)l, |
где Pi, Pf - четности начального и конечного ядер. Таким образом в случае
а) 0 < l < 5, четность не меняется и поэтому l = 0, 2, 4; в случае
б) 2 < l < 3, четность не меняется и l = 2; в случае
в) 0 < l < 5, четность не меняется и l = 0, 2, 4; и в случае
г) 1 < l < 4, четность меняется и l = 1, 3.
9. Используя значения масс атомов, определить верхнюю границу спектра позитронов, испускаемых при
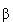 + -распаде ядра 27Si.
+ -распаде ядра 27Si.
Энергия 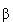 + - распада
+ - распада
Q = Mат.(A, Z) - Mат.(A, Z - 1) - 2 me,
где Mат.(A, Z) - масса атома исходного ядра и Mат.(A, Z - 1) - масса атома ядра-продукта (массы в энергетических единицах). Масса атома 27Si равна 25137.961 МэВ, а 27Al - 25133.150 МэВ. Верхняя граница спектра позитронов равна энергии распада
Tmax = Q = 25137.961 МэВ - 25133.150 МэВ - 2 х 0.511 МэВ = 3.789 МэВ.
10. Определить энергию отдачи ядра 7Li, образующегося при e- захвате в ядре 7Be. Даны энергии связи ядер - Eсв(7Be) = 37.6 МэВ, Eсв(7Li) = 39.3 МэВ.
Процесс 7Be + e- 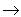 7Li +
7Li +  e. Энергия e -захвата
e. Энергия e -захвата
Qe = Eсв(A, Z-1) – Eсв(A, Z) – (mn – mp)c2 + mec2 = Eсв(A, Z-1) – Eсв(A, Z) – 0.78 МэВ,






