1. Одним из основных практически используемых свойств металлов и полупроводников является их электропроводность.
Основная количественная характеристика этого свойства – удельная электропроводность σ может быть определена через такие характеристики как заряд частицы q, концентрация n и подвижность носителей тока u.
Действительно, согласно закону Ома в дифференциальной форме, плотность электрического тока j во внешнем электрическом поле напряженности Е равна
j = σ ∙ E; (1)
С другой стороны
j = q∙n∙< v >, (2)
где < v > - средняя скорость направленного движения зарядов – носителей тока (скорость дрейфа).
Следовательно, согласно формулам (1) и (2)
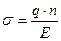·|< v >| = q·n·u,
где u = |< v >| / E - подвижность носителей тока.
Уровни Ферми.
Концентрация электронов в зоне проводимости (и образовавшихся дырок в валентной зоне) при заданной температуре Т пропорциональна вероятности "заполнения" электроном уровня Е при этой температуре.
Эта вероятность описывается функцией распределения Ферми–Дирака
,
в которой ЕF - энергия Ферми (или уровень Ферми), наименьшая энергия, необходимая для возбуждения одной частицы и перехода ее в зону проводимости. За начало отсчета энергии удобно выбрать (в энергетической диаграмме кристалла) нулевое значение.
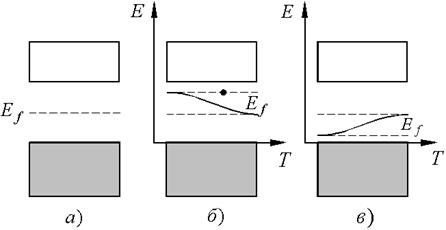
Рис.7.
а). Если в полупроводнике электрон "перебрасывается" с верхнего уровня валентной зоны на нижний уровень зоны проводимости, на это затрачивается энергия, равная ΔЕg (ширине запрещенной зоны). У чистого полупроводника при переходе электрона в зону проводимости в валентной зоне появляется другой носитель тока - дырка, т.е. на образование одного носителя тока необходима энергия ΔЕg/2. Следовательно, уровень Ферми чистого полупроводника расположен в центре запрещенной зоны (рис.7а).
б). Если вблизи нижнего края зоны проводимости расположены заполненные уровни примесных атомов (донорные уровни), то при сообщении электронам, находящимся на этих уровнях энергии ΔЕ1<<ΔЕg (рис.6а), эти электроны переходят в зону проводимости.
Энергия Ферми представляет собой среднюю энергию возбуждения электронов, "перебрасываемых" в зону проводимости. При абсолютном нуле и вблизи него уровень Ферми полупроводников-доноров расположен вблизи донорных уровней, т.к. в этой области температур переходы электронов через всю запрещенную зону (с верхнего уровня валентной зоны в зону проводимости) маловероятны.
Однако, с увеличением температуры вещества увеличивается число электронов, переходящих через всю запрещенную зону в зону проводимости, благодаря тепловому хаотическому движению и тепловым флуктуациям.
При каждом из таких переходов образуются два носителя тока (электрон и дырка). Следовательно, для образования одного носителя тока необходима энергия ΔЕg/2. Уровень Ферми перемещается (опускается) из области донорных уровней к своему предельному положению – в центр полосы запрещенных энергий (рис.7б).
в). В акцепторных полупроводниках при абсолютном нуле и вблизи него уровни Ферми расположены вблизи акцепторных уровней (у верхней границы валентной зоны). С увеличением температуры увеличивается число электронов, переходящих через всю запрещенную зону в зону проводимости, и уровень Ферми перемещается (поднимается), стремясь, как и в донорных полупроводниках, к своему предельному положению – в центр запрещенной зоны (рис.7в).
IV. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭЛЕКТРОПРОВОДНОСТИ.
1. Металлы. Удельная электропроводность металла σ, полученная на основе классической теории электропроводности, выражается формулой
,
где n - концентрация "свободных электронов", <λ> - их средняя длина свободного пробега, <ur> - средняя арифметическая скорость теплового хаотического движения.
В металле n и <λ> практически не зависят от температуры (при Т=0 К и температуре плавления концентрация электронов проводимости практически одинакова), а <ur> прямо пропорциональна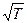 
, следовательно, согласно классической теории электропроводности, σ должна быть пропорциональна 
. Однако, экспериментально в широкой области температур получена зависимость 
, подтвержденная расчетами, проведенными на основе квантовой теории электропроводности.
В ней доказано, что внешнее электрическое поле ускоряет не все свободные электроны в металле (как принято считать в классической теории), а лишь электроны, находящиеся на уровне Ферми или вблизи него. Электроны на более "глубоких" уровнях не принимают участие в электропроводности.
Кроме того, следует учесть, что электроны проводимости перемещаются не только под действием внешнего электрического поля напряженности Е, но и в периодическом поле кристаллической решетки, действие которой следует учесть, введя эффективную массу электрона m*;
где 
- сила, обусловленная действием на электрон поля кристаллической решетки.
2. В чистом полупроводнике носителями тока также являются электроны проводимости, но механизм их возникновения отличается от механизма возникновения электронов проводимости в металлах.
Главные факторы их образования: тепловое хаотическое движение и наличие тепловых флуктуаций - отклонение энергий ионов (атомов) кристаллической решетки от их среднего значения (эти отклонения существуют при любой температуре, большей абсолютного нуля).
Такие атомы отдают валентные электроны, которые переходят через зону запрещенных энергий ΔЕg в зону проводимости. Поэтому при любой температуре, большей абсолютного нуля, в зоне проводимости полупроводника имеется некоторое количество электронов.
Одновременно с появлением в зоне проводимости электронов в ранее заполненной (валентной) зоне возникают дырки, перемещающиеся под действием внешнего электрического поля в направлении, противоположном перемещению электронов в зоне проводимости. При этом концентрации электронов и дырок одинаковы, nэ = nд = n, а суммарная плотность тока j, обусловленная движением электронов и дырок
,
где σ = n∙ e (uэ + uд),
uэ - подвижность электронов проводимости,
uд - подвижность дырок.
Для установления зависимости σ от Т, необходимо знать зависимость n, u э и uд от Т.
Концентрация электронов проводимости в полупроводнике при температуре Т пропорциональна вероятности заполнения уровня Е в зоне проводимости, которая определяется формулой
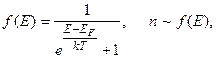
то есть 
где A - постоянная величина.
Примем E за нижнюю границу зоны проводимости, на которую переходит электрон с верхней границы валентной зоны Ев
Е = Ев +ΔЕg,
E = Ев +ΔЕg/2 (уровень Ферми расположен посередине ΔЕg)
Отсюда следует, что
Е - Е = ΔЕg/2, а 
При ΔЕg >> kT, 
, и, следовательно, концентрация электронов проводимости
Зависимость подвижности носителей тока (электронов и дырок) от температуры обусловлена рассеянием электронов при столкновении их с атомами (ионами) кристаллической решетки (при взаимодействии с атомами происходит изменение скорости электронов, как по величине, так и по направлению). С повышением температуры полупроводника тепловое хаотическое движение атомов становится интенсивнее, рассеяние увеличивается, подвижность носителей тока u = < v >/E (где <v> - средняя скорость направленного движения электронов) уменьшается.
Опытным путем, на основе исследования эффекта Холла, установлено, что в области температур Т≥Тс (Тс - температура собственной проводимости) температурная зависимость подвижных носителей тока в атомных полупроводниках имеет вид u ~ T -3/2, в ионных – u ~ Т –1/2.
Таким образом, при сравнении температурной зависимости n(T) и u(T) становится очевидной определяющая роль температурной зависимости n(T) в выражении для удельной электропроводности
σ = n∙e∙(uэ + uд), т.е. 
3. В примесных полупроводниках при Т< Тс проводимость обусловлена преимущественно наличием примесей (донорных или акцепторных); при Т≥Тс появляется собственная проводимость.
Удельная электропроводность такого полупроводника описывается выражениями:
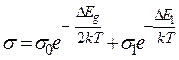
или
Первый член в выражении для σ − составляющая собственной проводимости, второй - примесной. В этом выражении ΔЕg - энергия диссоциации (ионизации) - ширина запрещенной зоны, ΔЕ1 и ΔЕ2 - энергии активации. У донорных примесей - это энергия, необходимая для перехода с донорного уровня на нижний уровень зоны проводимости (ΔЕ1, рис.6а), у акцепторных полупроводников - энергия, необходимая для перехода электрона с верхнего уровня валентной зоны (ΔЕ2, рис.6б).
В примесных полупроводниках при достаточно высоких температурах проводимость является собственной, а при низких – примесной.
V. P – N ПЕРЕХОД.
На границе непосредственного соприкосновения электронного и дырочного полупроводников возникает электронно – дырочный переход (p-n переход), который используется для изготовления полупроводниковых приборов.
В p-области контакта концентрация дырок гораздо больше, чем в n-области, поэтому, благодаря тепловому хаотическому движению, дырки диффундируют (совершают переход) из p-области в n-область, электроны, наоборот, из n-области в p. После "ухода" дырок из p-области в ней остаются отрицательно заряженные акцепторные атомы (возбужденный, но не занятый ранее уровень теперь занят электроном). С другой стороны, после ухода электронов из n-области в ней остаются положительно заряженные донорные атомы (с ранее заполненных донорных уровней "ушли" электроны).
Уровень Ферми в случае полупроводников n - типа сдвинут от середины запрещенной зоны вверх к зоне проводимости, а у полупроводников p - типа вниз к валентной зоне.
Так как акцепторные и донорные атомы малоподвижны (по сравнению с электронами и дырками), в области контакта полупроводников p- и n-типа образуется двойной слой пространственного заряда: отрицательный слой в p-области и положительный слой в n-области. Возникающее при этом контактное электрическое поле, характеризуется напряженностью 
, направленной из n в p-область (рис.8).
Рис. 8.
Это поле препятствует дальнейшему переходу (диффузии) основных носителей тока между p и n областями.
При тепловом равновесии и отсутствии внешнего электрического поля ток, обусловленный диффузией основных носителей (дырок в n-область и электронов в p-область), компенсируется током неосновных носителей, возникающим под действием контактного электрического поля .
Динамическое равновесие потоков основных и неосновных носителей тока, рассмотренное выше, нарушается под действием внешнего электрического поля 
.
Если p-область кристалла с p-n переходом подключить к положительному полюсу источника (рис.9), а n-область к отрицательному − равновесие потоков основных и неосновных носителей тока нарушается: усиливается диффузия дырок из p- в n-область и электронов из n- в p-область.
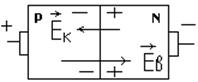
Рис. 9.
Через p-n-переход в направлении начинает течь ток, сила которого экспоненциально возрастает (прямой ток) с увеличением приложенного напряжения под действием внешнего электрического поля напряженности , причем ↑↓ , (рис.10, а).
Рис. 10
Если p-область кристалла с p-n-переходом подключить к отрицательному полюсу источника ↑↑ , резко увеличится поток основных носителей тока, диффундирующих через p-n контакт, в то время как поток неосновных носителей практически не изменится. Сила тока неосновных носителей очень мала (обратный ток) по сравнению с силой прямого тока (рис.10,б), возникающего при такой же (по модулю) разности потенциалов. Изменение знака напряжения U, поданного на p-n-переход, может изменить величину силы тока в 105 -106 раза. Благодаря этому кристаллы с p-n-переходом являются вентильным устройством, используемым для выпрямления переменного тока.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ
При подготовке к лабораторной работе в тетрадь необходимо внести:
- название работы и ее номер;
- цель работы;
- приборы и оборудование;
- теоретическую часть (кратко);
- таблицы, расчетные формулы и формулы расчета погрешностей.
При работе следует быть внимательным и выполнять правила техники безопасности. Инструкция по технике безопасности находится в лаборатории.
В процессе измерений результаты заносятся в тетрадь в виде таблиц, разрабатываемых самими студентами. В тех случаях, когда это рекомендуется, необходимо проводить графические построения.
Работа заканчивается составлением краткого заключения, в котором следует указать:
– что и каким методом исследовалось или определялось;
– полученные результаты и их погрешности (абсолютные и относительные);
– краткий анализ результатов и погрешностей.
ЛАБОРАТОРНАЯ РАБОТА 6.6
