Задача 2.1. Определить комплексное сопротивление Z, если  Oм,
Oм, 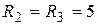 Oм,
Oм,  мкФ,
мкФ,  мГн,
мГн,  c-1.
c-1.
Решение:  ,
,
 где
где  , Ом;
, Ом;
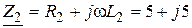 , Ом,
, Ом,  , Ом;
, Ом;
 .
.
Задача 2.2. Определить мгновенное значение тока  , если
, если  Oм,
Oм,  мкФ,
мкФ,  мГн,
мГн,  Oм,
Oм, 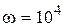 c-1,
c-1,  , В.
, В.
Решение: На основании закона Ома 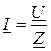 ;
;
 ,
,  ;
;
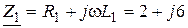 , Ом;
, Ом;

 , Ом;
, Ом;
 , Ом;
, Ом;
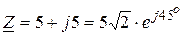 , Ом,
, Ом,  .
.
Отсюда  , А.
, А.
Задача 2.3. Определить мгновенное значение напряжения u, если
 Oм,
Oм,  мкФ,
мкФ, 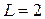 мГн,
мГн, 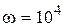 c-1,
c-1,  , В;
, В;

 , А.
, А.
Решение: На основании второго
закона Кирхгофа  ;
;
 , В;
, В;
 , Ом,
, Ом, 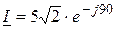 , А;
, А;
 .
.
 , В.
, В.
Задача 2.4. Дана цепь  Ом,
Ом, 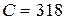 мкФ,
мкФ,  , В.
, В.
Определить  .
.
 |
Решение:  , А.
, А.
 , В.
, В.
Отсюда  , В.
, В.
Задача 2.5. Дана цепь 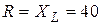 Ом,
Ом,  , В.
, В.
Определить  .
.
 |
Решение:  , А.
, А.
 , В.
, В.
Отсюда  , В.
, В.
 Задача 2.6. В цепи синусоидального тока все четыре вольтметра показывают одно и то же напряжение -
Задача 2.6. В цепи синусоидального тока все четыре вольтметра показывают одно и то же напряжение - 
 В. Определить
В. Определить  , если принять
, если принять  .
.
Решение:
Так как  , то
, то 
(в цепи резонанс напряжений).
Отсюда
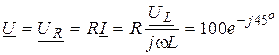 , В;
, В;
 , В.
, В.
Задача 2.7. Чему равно показание вольтметра  , включенного в цепь синусоидального тока, если вольтметр
, включенного в цепь синусоидального тока, если вольтметр  показывает
показывает 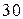 В,
В,  Ом,
Ом,  Ом.
Ом.
Решение:  В,
В,  А.
А.

Отсюда  В.
В.
Задача 2.8. Определить показания электромагнитного вольтметра, если 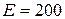 В,
В,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
 |
Решение: Вольтметр показывает
действующее значение напряжения
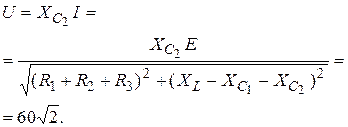
Задача 2.9. В цепи  , амперметр показывает
, амперметр показывает  А.
А.
 Определить
Определить  , если принять
, если принять  .
.
Решение: Из векторной диаграммы находим:
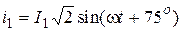 , А,
, А,
 ,
,
так как  ,
,
 то
то  ,
,
 А.
А.
Отсюда  , А.
, А.
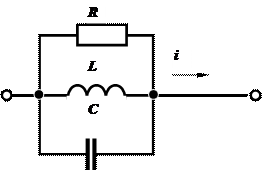 Задача 2.10. Определить
Задача 2.10. Определить 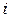 , если
, если  , В,
, В,  Ом,
Ом,  Ом.
Ом.
Решение:
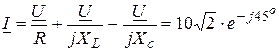 , А.
, А.
Отсюда  , А.
, А.
Задача 2.11. Определить показания амперметра  , если показания
, если показания
приборов  ,
,  ,
,  соответственно равны:
соответственно равны:  А,
А,  А,
А,  А.
А.
Решение: Из векторной диаграммы  А,
А, 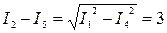 А.
А.
 Отсюда
Отсюда  А.
А.
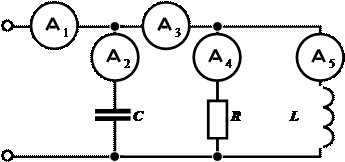
Задача 2.12. Определить параметры (L,R) катушки, используя результаты двух опытов:
1. При включении катушки в сеть постоянного тока U = 200 В, в катушке ток I = 5 А
2. При включении катушки в сеть переменного тока U = 200 В,
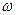 = 300 рад/сек., в катушке ток I = 4 А.
= 300 рад/сек., в катушке ток I = 4 А.
Решение:
Используя результаты 1-го опыта, получим 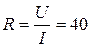 Ом.
Ом.
Используя результаты 2-го опыта, получим  Ом
Ом
Отсюда:  Ом;
Ом; 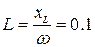 Гн
Гн
Задача 2.13. Определить xc, если U=200 В, ваттмер показывает 480 вт, амперметр 4 А
 Решение:
Решение:
Ваттметр показывает активную мощность 
Отсюда  Ом
Ом
Определив полное сопротивление цепи 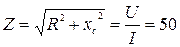 Ом
Ом
Находим  Ом
Ом
 Задача 2.14. Дана схема и векторная диаграмма токов в параллельных ветвях. Какие вектора надо сложить, чтобы получить показание амперметра?
Задача 2.14. Дана схема и векторная диаграмма токов в параллельных ветвях. Какие вектора надо сложить, чтобы получить показание амперметра?
Решение:
Амперметр покажет сумму токов:

На векторной диаграмме току 
соответствует вектор 2, току  - вектор 5, току
- вектор 5, току 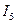 - вектор 1.
- вектор 1.
Следовательно, для получения показания амперметра необходимо сложить 1, 2 и 5 вектора.
Задача 2.15. По круговой диаграмме определить аргументы сопротивлений Z1 и Z2
Решение:

 ;
;
Если:  то
то  ;
;
Отсюда:  ;
;
Если:  то
то 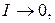
 ;
;
Отсюда: 
Задача 2.16. При каком значении xc в цепи возникает резонанс напряжений, если R=xL=4 Ом
Решение  :
:
Условие резонанса: 

 =0
=0
Отсюда xc=2 Ом
Задача 2.17. Определить R, при котором возникает резонанс токов, если x1=2 Ом, x2=4 Ом, x3=5 Ом
Решение  :
:
Условие резонанса: 
 ;
;  =0;
=0;
Отсюда R=2 Ом
Задача 2.18. Граничные частоты полосы пропускания последовательного контура  кГц,
кГц,  кГц. Входное напряжение равно 10 В. Определить напряжение на конденсаторе при резонансе.
кГц. Входное напряжение равно 10 В. Определить напряжение на конденсаторе при резонансе.
Решение:
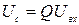 ;
; 
Отсюда  В
В
Задача 2.19. Реактор и конденсатор соединены последовательно. Найти напряжение на реакторе при резонансе, если входное напряжение равно 50 В, R=25 Ом, L=360 мГн, C=100 мкф
Решение:
 ;
;  ;
;  ;
;  ;
; 
Отсюда 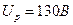
Задача 2.20. Максимальное и минимальное значение эквивалентной индуктивности последовательно соединённых одинаковых катушек равны соответственно 12 мГн и 6 мГн. Определить коэффициент связи.
Решение:
При согласном включении 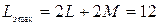 мГн
мГн
При встречном включении  мГн
мГн
Отсюда:  мГн,
мГн,  мГн,
мГн, 
Задача 2.21. Определить  , если вольтметр показывает 100 В, а
, если вольтметр показывает 100 В, а 
Решение: 

(так как  по условию)
по условию)
Отсюда:  В
В
Задача 2.22. Определить показание вольтметра, если амперметр
показывает 5 А. Катушки одинаковые  Ом,
Ом,  Ом, а
Ом, а
коэффициент связи равен единице.
Решение  :
:
По условию  Ом
Ом
Используя правило буравчика, определяем, что катушки включены встречно.
Отсюда: 
Показание вольтметра: 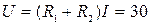 В
В
Задача 2.23. Выразить комплекс тока  , через
, через 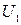 ;
;  ;
;  ;
; 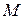 ;
; 
Активными сопротивлениями катушек пренебречь.
Решение  :
:
 (1)
(1)
 (2)
(2)
Решая уравнения (1) и (2) совместно, получим 
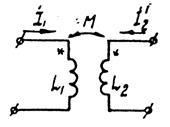 Задача 2.24. Определить реактивную мощность, передаваемую путём взаимной индукции из второй ветви в первую, если известны
Задача 2.24. Определить реактивную мощность, передаваемую путём взаимной индукции из второй ветви в первую, если известны 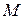 ;
;  ;
;  ;
; 
Решение:

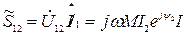 ,
, 
Отсюда: 
Задача 2.25. Определить токи в ветвях и составить уравнение баланса мощностей цепи.
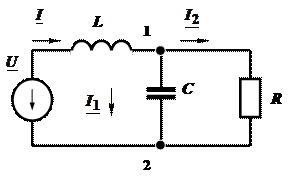 |
 , В,
, В,  Ом,
Ом,
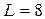 мГн,
мГн,  мкФ.
мкФ.
Решение:
На основании закона Ома 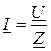 ;
;
 , В,
, В,
 Ом,
Ом,  А;
А;
 , А;
, А;  , А.
, А.
Уравнение баланса мощностей:
мощность источника 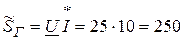 ;
;
 Вт,
Вт,  ;
;
мощность приемников:
 Вт;
Вт;
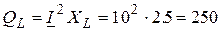 вар;
вар;
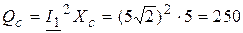 вар;
вар;
 ,
, 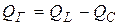 ;
;
 Вт =
Вт =  Вт,
Вт,  вар =
вар =  вар.
вар.
Задача 2.26. Определить токи в ветвях и составить уравнение баланса мощностей.
 , В,
, В,

 Ом,
Ом,
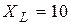 Ом,
Ом,
 Ом
Ом
Ответ:  , А,
, А,  ,А,
,А,
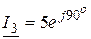 , А
, А
Задача 2.27. Определить токи в ветвях методом законов Кирхгофа.
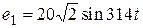 , В;
, В;
 , В;
, В;
 ,мкФ;
,мкФ;
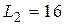 мГн,
мГн, 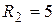 Ом,
Ом,
 Ом.
Ом.
Решение:



 ,
, 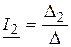 ,
, 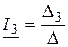 ;
;
 ;
;  ;
;
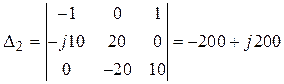 ;
;  ;
;
 , А,
, А,  А,
А, 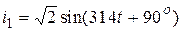 , А;
, А;
 ,
,  А,
А,  , А;
, А;  , А,
, А,  А,
А,  ,А;
,А;
Баланс мощностей:
 ;
;
 Вт;
Вт;
 Вт;
Вт;
 ,
,  ;
;
 Вт =
Вт =  Вт,
Вт,  вар =
вар =  вар.
вар.
Задача 2.28. Решить предыдущую задачу методом контурных токов.
Решение:
 где
где 
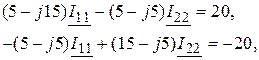


Задача 2.29. Определить токи в ветвях цепи методом законов Кирхгофа и методом контурных токов.
 , В;
, В;
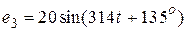 , В;
, В;
 мкФ,
мкФ,  мГн,
мГн,  Ом.
Ом.
Ответ: 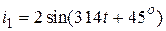 , А;
, А;

 , А;
, А;
 , А.
, А.
Задача 2.30. Определить  и
и  , если
, если  Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
 Решение: Собственное сопротивление
Решение: Собственное сопротивление
первого контура
 Ом.
Ом.
Взаимное сопротивление контуров
 , Ом.
, Ом.
Задача 2.31. Определить  , если
, если 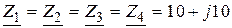 Ом;
Ом;  , В,
, В,
 , В.
, В.
 Решение: Собственная ЭДС контура
Решение: Собственная ЭДС контура

 Задача 2.32. Определить
Задача 2.32. Определить  и
и  , если
, если  , Ом.
, Ом.
Решение: Собственная проводимость
первого узла

Взаимная проводимость
 .
.
Задача 2.33. Определить  , если
, если

 Ом;
Ом;
 , В;
, В; 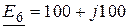 , В.
, В.
Решение: Собственный ток третьего узла
 , А.
, А.
Задача 2.34. Решить задачу методом двух узлов для определения токов.
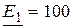 В,
В,  , В,
, В,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
Решение:


 ;
;
 ,
,  .
.
 Задача 2.35. Решить предыдущую задачу методом наложения.
Задача 2.35. Решить предыдущую задачу методом наложения.
Решение: 1. Расчет токов в цепи от действия 


2. Расчет токов в цепи от действия 
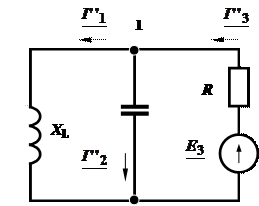
 , А;
, А;
 , А;
, А;
|
 , А.
, А.
Токи в ветвях исходной схемы:

Задача 2.36. Определить ток в  методом эквивалентного генератора.
методом эквивалентного генератора.
 (Схема задачи 2.21).
(Схема задачи 2.21).
Решение:
 ;
;
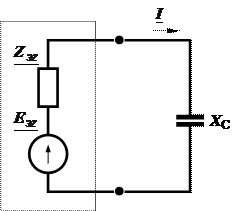
 ;
;
 .
.
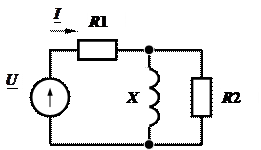
Задача 2.37. Определить  , при котором сдвиг фаз между
, при котором сдвиг фаз между  и
и  равен
равен  .
. 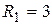 Ом,
Ом,  Ом.
Ом.
Решение:  ;
;  .
.
Чтобы сдвиг фаз был равен  , необходимо, чтобы:
, необходимо, чтобы:
 или
или
 .
.
Отсюда получаем уравнение:
 ,
,
решая которое находим  Ом.
Ом.
Задача2. 38. Дано: 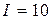 А,
А,  В,
В,  ,
,  .
.
Определить показания ваттметра.
Решение:  ;
;  ;
;
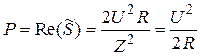
(так как  по условию);
по условию);
 А.
А.
 Отсюда
Отсюда  Ом.
Ом.
Следовательно  Вт.
Вт.






