Магнитное поле и его характеристики

Магнитное поле- это такое силовое поле, возникающее в пространстве, окружающем токи и постоянные магниты.

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в нем электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.

2. Закон Био — Савара — Лапласа для проводника с током I, элемент d l которого создает в некоторой точке А (рис. 164) индукцию поля d B, записывается в виде

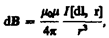(110.1)

где d l — вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r —радиус-вектор, проведанный из элемента d l проводника в точку А поля, r — модуль радиуса-вектора r. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление враще­ния головки винта дает направление d B, если поступательное движение винта соответ­ствует направлению тока в элементе.

Модуль вектора d B определяется выражением

(110.2)

где a — угол между векторами d l и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

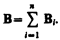(110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

3. Закон Ампера. Взаимодействие параллельных токов

 

Ампер установил, что сила d F, с которой магнитное поле действует на элемент проводника d l с током, находящегося в магнит­ном поле, равна

(111.1)

где d l —вектор, по модулю равный d l и совпадающий по направлению с током, В — вектор магнитной индукции.

Направление вектора d F может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца рас­положить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

(111.2)

где a —угол между векторами d l и В.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I ₁ и I ₂; (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из провод­ников создает магнитное поле, которое действует по закону Ампера на другой провод­ник с током. Рассмотрим, с какой силой действует магнитное поле тока I ₁ на элемент d l второго проводника с током I ₂. Ток I ₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. На­правление вектора B ₁ определяется правилом правого винта, его модуль по формуле (110.5) равен

Направление силы d F ₁, с которой поле B ₁ действует на участок d l второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол a между элементами тока I ₂ и вектором B ₁ прямой, равен

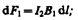
подставляя значение для В ₁, получим

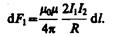(111.3)

Рассуждая аналогично, можно показать, что сапа d F ₂ с которой магнитное поле тока I ₂ действует на элемент d l первого проводника с током I ₁, направлена в проти­воположную сторону и по модулю равна

(111.4)

Сравнение выражений (111.3) и (111.4) показывает, что

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

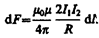(111.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).