Расчет частотных коэффициентов каждого узла системы обработки

сигналов и общего частотного коэффициента передачи

 

3.1 Расчет частотного коэффициента передачи оптической системы

 

С достаточной степенью точности полагают, что , где К₀ называют коэффициентом передачи. Наиболее распространенные варианты работы ОЭП – это работа на основе изменения освещенности входного зрачка (точечный источник) и изменение яркости свечения объекта (протяженный источник). В нашем случае дефект протяженный, поэтому

(3.1)

 

где А_ВХ – площадь входного зрачка фотоприемника;

– угловое поле зрения;

Lc – яркость источника излучения;

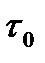–коэффициент отражения бумаги.

 

(3.2)

А_ВХ=

 

Тогда

(3.3)

3.2 Расчет частотного коэффициента передачи фотоприемника

 

В области малых и средних частот (f<10⁸ Гц) все фотоприемники считают с динамической точки зрения апериодическими звеньями первого порядка. В этом случае

 

, (3.4)

 

где Т_фп – постоянная времени фотоприемника;

Т_фп = с

S_инт – интегральная чувствительность по току;

S_инт = 0,2 А/Вт

 

Тогда

. (3.5)

3.3 Расчет частотного коэффициента передачи нагрузочной цепи

 

В случае использования нагрузочной цепи с трансформаторной связью частотный коэффициент передачи в области рабочих частот

 

, (3.6)

где ,

отсюда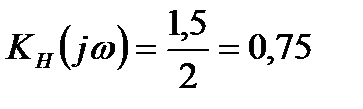

и – число витков вторичной и первичной обмоток трансформатора.

 

3.4 Расчет частотного коэффициента передачи усилителя

 

В общем случае частотные передаточные коэффициенты усилительного тракта могут быть весьма сложными и зависящими от функциональной и структурной схем электронного тракта усиления и обработки.

В усилительном тракте можно выделить несколько устройств, которые присутствуют практически во всех приборах неразрушающего контроля.

Прежде всего, это оптимальный фильтр, функции которого обычно выполняет один или несколько каскадов усилителя, квазиоптимальные фильтры (избирательные усилители) и полосовые фильтры.

Усилители мощности чаще всего имеют передаточный коэффициент:

 

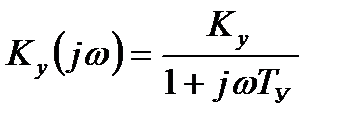, (3.7)

 

 

где К_У – коэффициент усиления;

Ту – постоянная времени, примем Ту=10^-7 с.

Эффективная полоса пропускания

=2∙10⁷ 1/c. (3.9)

Отсюда

, (3.10)

 

Рассчитаем общий частотный коэффициент передачи:

 

(3.11)

 

.

 

График зависимости частотного коэффициента передачи представлен в приложении А.

 

4 Расчет спектра входного сигнала

 

В задании сказано, что модуляция зондирующего сигнала производится механическим способом. Примем частоту модуляции выбираем из полосы пропускания фильтра с^-1. Рассчитаем длительность зондирующего импульса.

. (4.1)

Определим период зондирующего сигнала

 

. (4.2)

 

Найдем длительность зондирующего импульса. Так как диск модулятора имеет такой вид (рисунок 4.1)

 

Рисунок 4.1 – Вид диска модулятора

 

Зная период, можно найти длительность импульсов

 

 

, (4.3)

 

Время контроля примем равным 3 с, найдем количество импульсов за время контроля

 

(4.4)

 

Построим модель входного сигнала во временной области (Рисунок 4.2).

 

 

Рисунок 4.2 – Входной сигнал во временной области

 

 

Так как нам необходимо знать только модуль спектра сигнала на входе, мы можем воспользоваться готовой формулой для модуля спектра сигнала, представляющего собой последовательность прямоугольных импульсов/3/

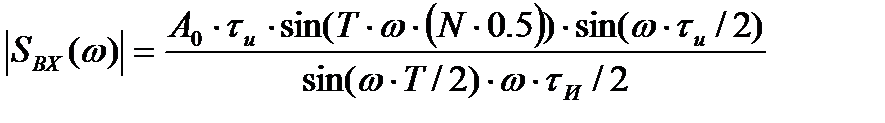, (4.5)

 

где А₀ – амплитуда импульсов, А₀=Ф_Е =10 ^{- 2} Вт;

t_И=Т/2 – длительность импульсов;

Т – период следования импульсов;

N – количество импульсов за время контроля.

В результате получаем

(4.6)

 

График зависимости спектра на входе устройства представлен в приложении А.

 

 

5 Расчет спектра на выходе устройства обработки сигналов

Спектр сигнала на выходе устройства обработки рассчитывается по следующей формуле:

 

S_ВЫХ=К_ОЭП(jω)∙S_ВХ(ω) (5.1)

График зависимости спектра на выходе устройства 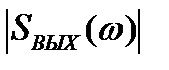представлен в приложении А.

 

6 Расчет значений действующих шумов в тракте обработки сигналов

Внешние помехи обычно зависят от параметров оптической системы и обусловлены как правило радиационным и фотонным шумами. Радиационные и фотонные шумы возникают вследствие статистического характера потока излучения, представляющего случайную совокупность потока квантов энергии электромагнитного поля.

Радиационные и фотонные внешние помехи при частотах менее 10¹⁰ Гц можно считать белыми шумами, мощность которых постоянна во всей области рассматриваемых частот.

 

W_Б.Ш(ω)=10^-3∙Ф_ФП= (Вт) (6.1)

 

Спектральная плотность мощности радиационных и фотонных помех, приведенных ко входу в полосовой фильтр определяется выражением, справедливым для обоих случаев:

 

(6.2)

 

Ко внутренним шумам, зависящим от параметров оптической системы, относятся шумы, генерируемые в самих фотоприемниках, и зависящие от протекающего в них тока. К ним относятся дробовые, токовые и генерационно - рекомбинационные шумы. Сюда же относятся тепловые шумы. Состав и количественные параметры спектральных плотностей мощности этих шумов зависят от типа применяемого фотоприемника. В общем виде спектральные плотности мощности перечисленных составляющих шумов представляются в виде:

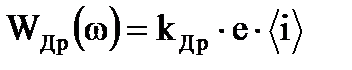, (6.3)

где k_Др=1;

е – заряд электрона; е=1,6 *10^-19Кл;

- среднее значение тока на выходе фотоприемника;

, (6.4)

где R_фп – внутреннее сопротивление теплового ФП, равно 100 Ом.

Отсюда

(Вт) (6.5)

Для токового шума спектральная мощность:

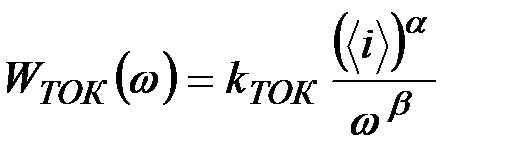, (6.6)

где k_ТОК - коэффициент, зависящий от конкретного образца фотоприёмника,

k_ТОК=1;

α=2;

β=1.

Подставим числовые значения:

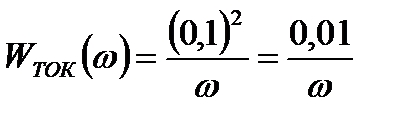(Вт) (6.7)

 

Для генерационно - рекомбинационного шума спектральная мощность будет иметь следующий вид:

, (6.8)

где Т_н – среднее время жизни носителей заряда в полупроводниковых ФП, Т_н =

К_Г-Р - коэффициент, зависящий от конкретного образца фотоприёмника, К_Г-Р =1.

Подставим числовые значения:

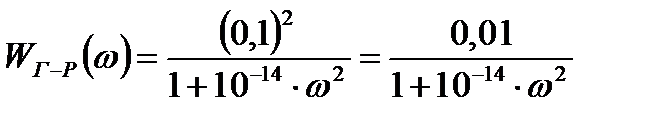(Вт) (6.9)

 

 

Для теплового шума спектральная мощность имеет вид:

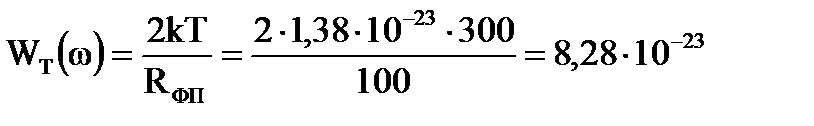(Вт), (6.10)

где k – постоянная Больцмана (1,38^.10^-23 Дж/к);

Т – температура фотоприемника, °К;

 

(6.11)

Подставляя величины, получим:

 

Так как у нас в формуле имеются сравнительно малые величины, то мы ими можем пренебречь. Тогда

 

(Вт) (6.12)

Спектральная плотность мощности шумов ФП, приведенная ко входу оптимального фильтра составляет:

 

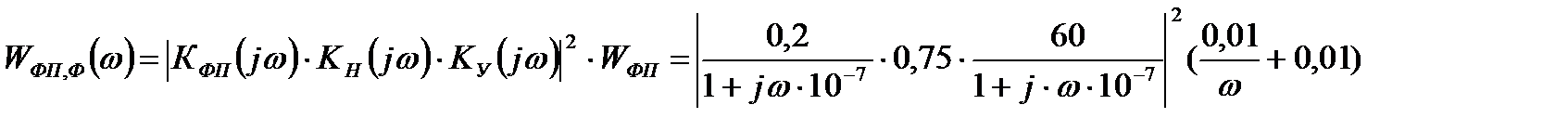(6.13)

К внутренним помехам, не зависящим от параметров оптики, относятся шумы, генерируемые активными сопротивлениями нагрузочной цепи и в элементах электронного тракта усилителя. При этом достаточным бывает учитывать шумы, генерируемые в первом каскаде усилительного тракта. Именно здесь полезный сигнал имеет еще малые значения по сравнению с генерируемыми шумами. На входе в усилитель шумы нагрузочной цепи и первого каскада усилителя представляются в виде:

 

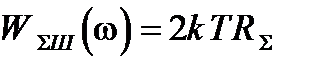
(Вт), (6.14)

где R_S – суммарное эквивалентное шумовое сопротивление элементов нагрузочной цепи и первого каскада усилителя, 100 Ом

Т – температура элементов электронного тракта (Т=300°К).

Спектральная плотность мощности этих помех, приведенных ко входу в полосовой фильтр:

 

. (6.15)

В этой формуле также пренебрегаем малыми числами.

Тогда

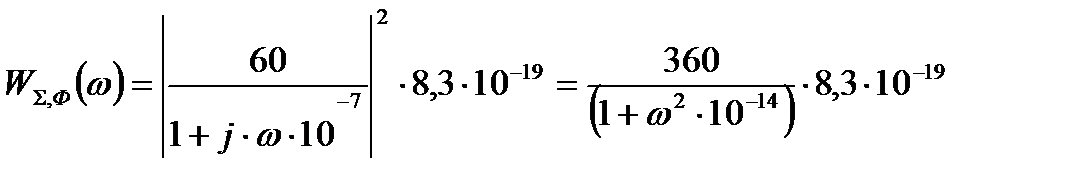(Вт),

Таким образом, определены все составляющие помехи и приведены ко входу фильтра низких частот.

 

Тогда

 

(6.16)

(Вт),

График зависимости действующих шумов в тракте устройства обработки сигналов представлен в приложении А.

7 Расчет необходимого значения сигнал/шум и порогового уровня принятия решения по заданным параметрам обнаружения дефектов

 

Расчет необходимого соотношения сигнал/шум и порогового уровня принятия решения необходимо производить в зависимости от вида исходных данных: допустимого значения вероятности ложной тревоги, средней частоты или среднего периода появления ложной тревоги, или вероятности появления хотя бы одной ложной тревоги за определенное время наблюдения. При этом будет найден пороговый уровень принятия решения о наличии дефекта. Увеличивать вероятность правильного обнаружения дефекта можно за счет выбора значения соотношения сигнал/шум большего, чем пороговое значение. В этом случае необходимо рассчитать вероятность правильного обнаружения. В данной курсовой работе дана средняя частота появления ложной тревоги при обнаружении дефектов в изделии . Когда задана эта величина, то необходимо рассчитать величину ρ_n

(7.1)

(7.2)

Подставив значения получим

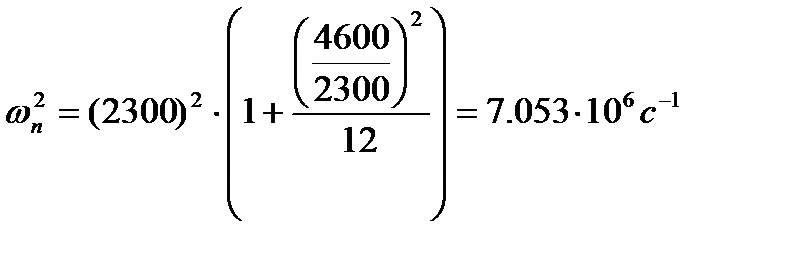
После выяснения значения относительного порога, равного 5.23, приступим к нахождению вероятности правильного обнаружения в случае, когда отношение сигнал/шум на выходе превышает величину параметра обнаружения

 

, (7.3)

где – вероятность правильного обнаружения дефекта;

ρ – создаваемое на выходе прибора отношение сигнал/шум;

Ф – интеграл вероятности.

Подставим числовые значения:

 

 

 

 

.

 

 

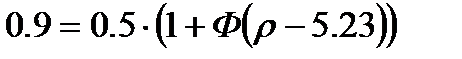
8 Расчет основных параметров устройства обработки сигналов по требуемому отношению сигнал/шум

Решим основное энергетическое уравнение:

 

. (8.1)

где полезным является применение теоремы Парсеваля, которая следует из формулы Релея. Она определяет равенство энергий сигналов при их представлении в частотной и временной областях:

 

,

 

где tk – время контроля;

N– число импульсов, N=1195

- длительность импульса,

А₀ – амплитуда импульсов, А₀=Ф_Е =10 ^{- 2} Вт;

Считаем, что W_ВХ(ω)= , т.к. на продолжительной частоте почти не меняется значение спектральной мощности помех. Поэтому можем считать, что это белый шум. После чего имеем:

 

Рассчитанное отношение сигнал/шум 7,63 превышает необходимое отношение сигнал/шум 6.53, что доказывает правильность выбора данной пары – излучающий диод АЛ112А – фотодиод ФД-21-КП и соответствие характеристик этих элементов поставленной задаче.

 

9 Расчет пороговой чувствительности

Значение пороговой чувствительности определяется из соотношения:

Следовательно:

(А/Вт).

(9.1)

 

10 Расчет информационного содержания сигнала на выходе устройства

Расчет информационного содержания непрерывного сигнала может быть произведен в предположении, что функция распределения плотности вероятностей соответствует нормальному закону распределения. При количественной оценке информационного содержания дискретных сигналов следует обращать внимание на количество уровней и число этих сигналов.

Если на устройство контроля следует информационный сигнал Х вместе с помехой Y, то количество информации I, получаемое приемником в этих условиях можно определить по формуле:

 

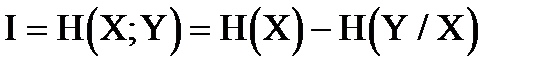, (10.1)

где Н(Х) – энтропия полезного сигнала;

Н(Y/Х) – условная энтропия.

Поскольку решающее устройство фиксирует факт наличия или отсутствия сигнала, то имеем:

 

, (10.2)

где Р – вероятность правильного обнаружения сигнала Р=0,9.

Подставим числовые значения:

 

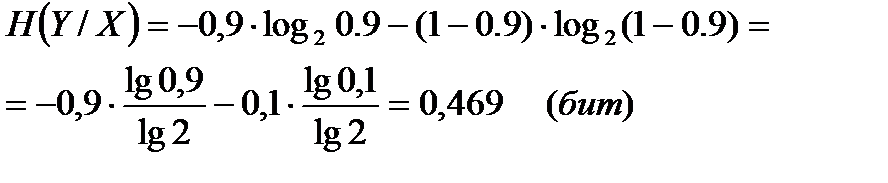(10.3)