абораторна робота №17
 |
ДОСЛІДЖЕННЯ КОЛИВАНЬ СТРУНИ
Мета роботи
Вивчити явище утворення стоячих хвиль у струні, знайти частоти власних коливань та швидкість поширення хвиль у струні при фіксованій силі натягу.
Прилади та обладнання
Звуковий ґенератор, віброперетворювач, струна, нерухомий блок, масштабна лінійка, тягарці.
Опис вимірювального пристрою
 |
|
навантажено основним тягарцем (4). Накладаючи на тягарець (4) додаткові тягарці, можна змінювати силу натягу струни. Довжина L частини струни, яка здійснює механічні коливання, дорівнює віддалі між нижньою точкою закріплення та точкою дотику струни до блоку, і надалі буде вважатися довжиною струни. Частоту (у звуковому діапазоні) і амплітуду коливань вихідного сигналу звукового ґенератора можна регулювати за допомогою відповідних ручок на його передній панелі. Координати вузлів та пучностей стоячої хвилі, а також її довжину визначають масштабною лінійкою (6).
Виведення розрахункових формул
Збуджені вібратором поперечні коливання струни поширюються до верхньої точки закріплення струни. Тут хвиля відбивається і рухається у зворотньому напрямі. В результаті у струні виникають стоячі хвилі. При цьому точки закріплення струни є одночасно вузлами стоячої хвилі, оскільки стоячі хвилі виникають тільки при таких частотах, коли на довжині струни L вкладається ціле число півхвиль, тобто ціле число довжин стоячої хвилі.
Звідси випливає, що
або 
, (1)
де n = 1, 2, 3...
Відповідні власні частоти коливань струни зв’язані з довжиною хвилі співвідношенням:
νn 
, (2)
де u - швидкість поширення хвиль у струні, однакова для всіх частот.
Найнижча частота ν1 
називається основним тоном коливань або першою гармонікою. Всі вищі частоти, кратні до ν1, називаються обертонами, наприклад: подвоєна частота ν2 = 2ν1 – це перший обертон або друга гармоніка і т.д.
Вигляд струни у випадку спостереження основного тону та першого і другого обертонів подано на рис.2.
|
 |
Швидкість поширення поперечних хвиль у струні залежить від сили натягу струни:
= 
= 
= 
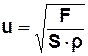. (3)
де F = mтg - сила натягу струни (mт – маса тягарця),
– густина матеріалу струни (m – маса струни, V – її об’єм),
S - площа поперечного перерізу струни, L – довжина струни.
Позначивши 
- маса одиниці довжини струни, або лінійна густина струни, одержимо:
. (4)
Враховуючи (4), для частот коливань струни отримаємо вираз:
νn 
, (5)
де n = 1, 2, 3...
Виберемо за початок відліку одну із точок закріплення струни і вісь х спрямуємо вздовж струни. Тоді рівняння стоячої хвилі, що виникає у струні при частоті νn, запишемо у вигляді:
n = 2A sin k(L-x) cos(kL - 
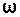t) = Acт cos(
n – ωt), (6)
де n - поперечне відхилення точки струни з координатою x у момент
часу t;
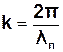- хвильове число;
Acт = 2A|sin 
(L-x)| - амплітуда стоячої хвилі
З умови (L-xп) = (2m+1)π знаходимо координати пучностей (Аст = 2А) стоячої хвилі: xn=[n-(m+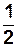 
)] 
. (7)
З умови (L-xв) = mπ знаходимо координати
вузлів (Аст =0) стоячої хвилі: xв = (n – m) (8)
В таблиці наведені координати пучностей xn і вузлів xв для основного тону (n=1) і вищих гармонік (n=2,3).
| n | m | xn | xв |
| 1 ∕2 L | L | ||
| 3∕4 L 1∕4 L | L | ||
| 1∕2L | |||
| 5∕6 L 1∕2 L 1∕6 L | L | ||
| 2∕3 L | |||
| 1∕3 L | |||
При підготовці до виконання роботи використати:
еоретична частина. Розділ 3.7.
Послідовність виконання роботи
1. Увімкнути звуковий ґенератор (ЗҐ), прогріти його протягом 5 хв. Ручкою регулювання частоти встановити мінімальну частоту.
2. Збільшуючи частоту ЗҐ, одержати стоячу хвилю, що відповідає основному тону коливань струни. Записати відповідну частоту ЗҐ (νд) у таблицю. (Частоту власних коливань струни можна вважати рівною частоті сигналу ЗҐ при максимальній амплітуді коливань струни (резонанс)). Перевірити узгодження координат вузлів і пучностей з (7) та (8).
3. Поступово збільшуючи частоту ЗҐ, одержати перший та другий обертони (n = 2, 3,). Провести вимірювання, аналогічні п.2.
4. Накласти на основний тягарець один додатковий тягарець і повторити вимірювання п.п. 2, 3.
5. Додати другий додатковий тягарець і ще раз повторити вимірювання п.п. 2, 3.
6. За формулою (5) розрахувати частоти власних коливань струни νр, результати записати у таблицю.
7. Визначити абсолютну і відносну похибки вимірювань, як:
Δν 
(Δν1+Δν2+Δν3)= 
(½νр- νД1½+½νр- νД2½+½νр- νД3½)
δν =(Δν/νр) ×100%
8. За формулою (4) розрахувати швидкості поширення хвиль у струні при різних силах натягу; результати записати у таблицю.
лінійна густина струни mL = 600 ×10-6 г/м, маса основного тягарця 250 г,
маси додаткових тягарців 50 г і 65 г.
Таблиця результатів вимірювань і розрахунків
| n | = | n | = | n | = | ||||||||||
| № | mт, г | νд, Гц | νр, Гц | Δν Гц | δν % | νд, Гц | νр, Гц | Δν Гц | δν % | νд, Гц | νр, Гц | Δν Гц | δν % | u, м/с | |
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | роз. | |||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| сер. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | ||||||
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | роз. | |||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| сер. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | ||||||
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | роз. | |||||||||
| вим. | роз. | вим. | роз. | вим. | роз. | ||||||||||
| сер. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | роз. | ||||||
Контрольні запитання
1. Вивести рівняння стоячої хвилі.
2. В якому випадку можливе виникнення стоячих хвиль?
3. Чому дорівнює амплітуда стоячої хвилі?
4. З яких умов знаходимо координати вузлів та пучностей?
5. У яких точках струни швидкість коливань буде максимальною?
6. Як впливає величина сили натягу на частоту власних коливань струни?
Рекомендована література
1. Курс фізики / За редакцією І.Є.Лопатинського.
– Львів: Вид. «Бескид Біт», 2002.
2. Трофимова Т.И. Курс физики.– М.: Высшая школа, 1990.
3. Савельев И. В. Курс общей физики, т.2 –М.: Наука, 1982.
