Виды проецирования. Центральное и параллельное проецирование.
1. Центральное проецирование – проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис.1).
2. Параллельное проецирование – проецирующие лечи параллельны и составляют с плоскостью угол 90% (прямоугольное проецирование рис.2) и угол отличный от 90 % (косоугольное проецирование рис.3).

Рис.1 Рис.2 Рис.3
Аппарат проецирования включает в себя:
Пi - плоскость проекций,
S - центр проецирования,
А - объект проецирования (точка),
SA - проецирующую прямую,
Ai - проекцию точки А.
Метод Монжа. Ортогональные проекции точки на две и три плоскости проекций.
Образование чертежа точки в системе двух и трех плоскостей проекций
Метод Монжа
Данный метод позволяет определить место каждой точки изображения относительно других точек.
Точку (предмет) помещают в систему двух взаимоперпендикулярных плоскостей, которые используются в качестве плоскостей проекций.
П1 – горизонтальная плоскость проекций;
П2 – фронтальная плоскость проекций;
х – ось проекций: х = П1 ∩ П2.
Плоскости проекций П1, П2 делят пространство на четыре части, называемые четвертями. Точка А находится в I четверти пространства. Проведя перпендикуляры к П1 (A Î s’ ┴ П1, A1 = s’ ∩ П1) и П2 (A Î s” ┴ П2, A2 = s” ∩ П2), получаем проекции точки А (рис.4):
А1 – горизонтальная проекция точки А,
А2 – фронтальная проекция точки А.
Если даны проекции А1 и А2 некоторой точки А, то проведя перпендикуляры: через т.А1 к плоскости П1 (s’ ┴ П1), а через т. А2 к П2 (s” ┴ П2), получим в пересечении этих прямых определенную точку А (s’ ∩ s” = A) (рис.5).
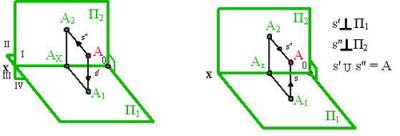
Рис.4 Рис.5
Вывод: Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.
Вращением вокруг оси Ох плоскость П1 совместим с плоскостью П2. При этом проекции А2 и А1 точки А расположатся на одном перпендикуляре к оси проекций – на линии связи.

Рис.6
В результате указанного совмещения плоскостей П2 и П1 получается чертеж, известный под названием эпюр Монжа или двухкартинный чертеж, включающий две взаимосвязанные проекции - “картины”. Это чертеж в системе П1, П2 или в системе двух прямоугольных проекций. Условимся в дальнейшем двухкартинный чертеж, а также чертеж, в основе которого лежит метод Монжа, называть одним словом – чертеж и понимать это только в указанном смысле. В других случаях применения слова «чертеж» оно будет сопровождаться соответствующим определением (перспективный чертеж, аксонометрический чертеж и т.п.).
Известно, что чертежи сложных конструкций содержат не две, а большее число изображений – проекций. Рассмотрим введение в систему П1, П2 еще одной плоскости проекций, перпендикулярной П1 и П2 (рис.7):
П3 – профильная плоскость проекций;
х = П1 ∩ П2; у = П1 ∩ П3; z = П2 ∩ П3; О = х ∩ у ∩ z.
Опустим перпендикуляр на плоскость П3 из точки А и получим:
А3 – профильную проекцию точки А (рис.8)

Рис.7 Рис.8
Для получения трехкартинного чертежа точки надо повернуть плоскость П1 вокруг оси x и плоскость П3 вокруг оси z до совмещения их с плоскостью П2 (рис.9).

Рис.9
Выводы:
1. Каждая точка пространства характеризуется тремя координатами: А (х, у, z).
2. Каждая проекция точки на чертеже – двумя координатами: А1 (х, у); А2 (х, z); А3 (у, z).
3. Две проекции точки однозначно определяют ее положение в пространстве.






