Задача прикрепления потребителей к поставщикам (транспортная задача)

Задача о пищевом рационе

Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П₁, П₂, П₃, П₄; стоимость единицы каждого продукта равна соответственно с₁, с₂, с₃, с₄. из этих продуктов требуется составить пищевой рацион, который должен содержать: белков – не менее b₁ единиц; углеводов – не менее b₂ единиц; жиров – не менее b₃ единиц. Для продуктов П₁, П₂, П₃, П₄ содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где a_ij (i = 1, 2, 3, 4, j = 1, 2, 3) – какие-то определенные числа; первый индекс указывает номер продукта, второй – номер элемента (белки, углеводы, жиры).

 

Продукт	Элементы
Белки	Углеводы	Жиры
П1	a11	a12	a13
П2	a21	a22	a23
П3	a31	a32	a33
П4	a41	a42	a43

 

Требуется составить такой пищевой рацион (то есть назначить количества продуктов П₁, П₂, П₃, П₄, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель. Обозначим х₁, х₂, х₃, х₄ количества продуктов П₁, П₂, П₃, П₄, входящих в рацион. Показатель эффективности, который требуется минимизировать, – стоимость рациона (обозначим ее L); она линейно зависит от элементов решения х₁, х₂, х₃, х₄:

L= с₁х₁+ с₂ х₂+ с₃ х₃+ с₄ х₄,

Или, короче,

,

Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам, жирам. Учитывая, что в одной единице продукта П₁ содержится a₁₁ единиц белка, в х₁ единицах - a₁₁ х₁ единиц белка, в х₂ единицах продукта П₁ содержится a₂₁ х₂ единиц белка и т.д., получим три неравенства:

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х₁, х₂, х₃, х₄.

Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х₁, х₂, х₃, х₄,, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в минимум линейную функцию этих переменных:

 

Задача о планировании производства

предприятие производит изделия трех видов U₁, U₂, U₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия U₁, не менее b₂ единиц изделия U₂ и не менее b₃ единиц изделия U₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: β₁, β₂, β₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья s₁, s₂, s₃,, s₄, причем запасы ограничены числами γ₁, γ₂, γ₃, γ₃ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_ij количество единиц сырья вида s₁ (i = 1, 2, 3, 4), потребное на изготовление одной единицы изделия U_j (j = 1, 2, 3). Первый индекс у числа a_ij – вид изделия, второй – вид сырья. Значения a_ij сведены в таблицу (матрицу).

 

Сырье	Изделия
U1	U2	U3
s 1	a11	a21	a31
s 2	a12	a22	a32
s 3	a13	a23	a33
s 4	a14	a24	a34

 

При реализации одно изделие U₁ приносит предприятию прибыль с₁, U₂ – прибыль с₂, U₃ – прибыль с₃. Требуется так спланировать производство (сколько и каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась бы в максимум.

Запишем задачу в форме задачи линейного программирования. Элементами решения будут х₁, х₂, х₃ – количества единиц изделий U₁, U₂, U₃, которые мы произведем. Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств:

Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства:

Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства:

 

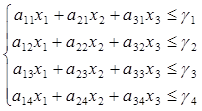
Прибыль, приносимая планом (х₁, х₂, х₃), будет равна

L= с₁х₁+ с₂ х₂+ с₃ х₃.

Таким образом, мы снова получили задачу линейного программирования: найти такие неотрицательные значения переменных х₁, х₂, х₃,, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в максимум линейную функцию этих переменных:

.

 

Задача прикрепления потребителей к поставщикам (транспортная задача)

Рассмотрим проблему организации перевозки некоторого условного продукта между пунктами его производства, количество которых равно m, и n пунктами потребления. Каждый i –й пункт производства (i = 1,…, m) характеризуется запасом продукта а_i ≥0, а каждый j- ый пункт потребления (j = 1,…, n) – потребностью в продукте b_j ≥0. Сеть коммуникаций, соединяющая систему рассматриваемых пунктов, моделируется с помощью матрицы С размерности m×n, элементы которой (с_ij) представляют собой нормы затрат на перевозку единицы груза из пункта производства A_i в пункт потребления B_j. То есть задана таблица (матрица):

 

bj аi	B1	B2	…	Bn
A1		c11		c12	…		c1n	a1
A2		c21		c22	…		c2n	a2
…	…	…	…	…	…
Am		cm1		cm2	…		cmn	am
	b1	b2	…	bn

 

Строки транспортной таблицы соответствуют пунктам производства А_i (в последней клетке каждой строки указан объем запаса продукта a_i), а столбцы – пунктам потребления В_j (последняя клетка каждого столбца содержит значение потребности b_j). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i –го пункта производства в j –ый пункт потребления.

План перевозки груза в данной транспортной сети представляется в виде массива элементов размерности m×n:

.

Ограничения на возможные значения х_ij имеют вид:

1) ограничения на удовлетворение потребностей во всех пунктах потребления:

(*)

2) ограничения на возможности вывоза запасов из всех пунктов производства:

(**)

3) условия неотрицательности компонент вектора плана х:

Существенной характеристикой описываемой модели является соотношение параметров а_i и b_j. Если суммарный объем производства равен суммарному объему потребления, а именно,

,

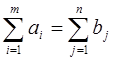то система называется сбалансированной (или говорят, что имеют закрытую транспортную задачу). При выполнении условия сбалансированности разумно накладывать такие ограничения на суммарный ввоз и вывоз груза, при которых полностью вывозится весь груз и не остается неудовлетворенных потребностей, то есть условия (*) и (**) приобретают форму равенств.

Предположим, что затраты на перевозку прямо пропорциональны количеству перевозимого груза. Тогда суммарные затраты на перевозку в системе примут вид:

Тогда модель транспортной задачи имеет вид:

или в подробном виде:

 

Если привести условия транспортной задачи к канонической форме задачи линейного программирования, то матрица задачи будет иметь размерность (m+n) ×mn. Ранг матрицы задачи равен m+n-1, и ее невырожденный базисный план план должен содержать m+n-1 ненулевых компонент.