Задачи к экзамену по математике для ПИЭ-21, ИСТ-21, 22.
Ι. Комплексные числа
Задача 1. Даны комплексные числа 
и 
.
1) Найти их сумму, разность, произведение и частное в алгебраической форме.
2) Представить эти числа в тригонометрической форме и найти:
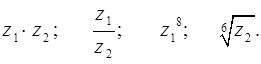
3) Представить эти числа в показательной форме.
Задача 2. Решить уравнения: 
; 
.
ΙΙ. Векторы на плоскости и в пространстве
Задача 3. Даны три вектора 
. Найти длину вектора 
и разложить вектор 
по векторам 
и 
.
Задача 4. Даны векторы 
, 
, 
, 
. Приняв в качестве базиса векторы , , 
, найти разложение вектора 
по этому базису.
Задача 5. Даны векторы 
и 
. Найти: 1) векторы 
, 
; 2) длины векторов и ; 3) скалярный квадрат вектора ; 4) скалярное произведение 
; 5) угол между векторами и .
Задача 6. Даны вершины треугольника 
, 
, 
. Вычислить длину его высоты, опущенной из вершины 
на сторону 
.
Задача 7. Выяснить, являются ли компланарными векторы:
а) 
, 
, 
; б) 
, 
, 
.
Задача 8. Вычислить объем тетраэдра с вершинами в точках 
, 
, 
, 
и его высоту, опущенную из вершины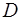 
на грань 
.
ΙΙΙ. Прямая линия на плоскости
Задача 9. Составить уравнение прямой, проходящей через точку 
: а) под углом 
к оси 
; б) параллельно оси 
; в) и точку 
.
Задача 10. Даны вершины треугольника 
. Найти координаты точки пересечения медиан треугольника.
Задача 11. Дан треугольник с вершинами в точках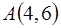 
, 
, 
. Записать уравнения всех его сторон и высоты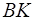 
в общем виде, в нормальном виде, как уравнение прямой с известным угловым коэффициентом.
ΙV. Плоскость, различные виды ее уравнений
Задача 12. Написать уравнение плоскости, параллельной вектору 
и проходящей через точки 
и 
.
Задача 13. Вычислить расстояние от точки 
до плоскости 
.
Задача 14. Дана треугольная пирамида с вершинами в точках 
, 
, 
, 
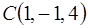. Найти длину высоты 
.
Задача 15. Составить уравнение плоскости, проходящей через точку 
, параллельно плоскости 
.
Задача 16. Найти расстояние от точки 
до плоскости, проходящей через три точки 
.
V. Прямая линия в пространстве
Задача 17. Привести общие уравнения прямой 
к каноническому виду.
Задача 18. Составить уравнение прямой, проходящей через точку 
и:
а) образующей с осями координат углы 
;
б) параллельной прямой 
;
в) параллельной оси ;
г) параллельной прямой 
;
д) точку 
.
Задача 19. Составить канонические уравнения прямой, проходящей через точку 
перпендикулярно плоскости, походящей через точки 
.
VΙ. Линии второго порядка на плоскости
Задача 20. Записать уравнение окружности, если координаты концов одного из диаметров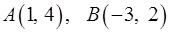 
.
Задача 21. Определить радиус и центр окружности, данной уравнением 
и построить ее.
Задача 22. Дано уравнение линии второго порядка 
. Найти полуоси, координаты фокусов, эксцентриситет, уравнения директрис. Построить линию.
Задача 23. Дано уравнение линии второго порядка 
. Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис. Построить линию.
Задача 24. Найти параметр, координаты фокуса, уравнение директрисы параболы 
.
Задача 25. Вычислить длину хорды, образуемой пересечением прямой 
с параболой 
.
Задача 26. Привести уравнение кривой второго порядка 
к каноническому виду и найти точки ее пересечения с прямой 
. Построить графики кривой и прямой.
