¬ведение
ѕри конструкторском проектировании электронных средств (Ё—) решаютс€ задачи, св€занные с поиском наилучшего варианта конструкции, удовлетвор€ющего требовани€м технического задани€ и максимально учитывающего возможности технологической базы производства. “есна€ взаимосв€занность задач и больша€ размерность каждой из них обычно не позвол€ет предложить метод поиска оптимального конструктивного решени€ в едином цикле в св€зи с трудност€ми создани€ общей математической модели, комплексно учитывающей особенности конструкторско-технологической базы производства. ѕоэтому разработка и реализаци€ алгоритмов и методов решени€ отдельных задач этапа конструкторского проектировани€: компоновки, размещени€ и трассировки, Ц до сих пор остаютс€ актуальными проблемами, решение которых неотъемлемо св€зано с развитием систем автоматизации проектировани€.
I раздел. “еоретическа€ часть
«адача компоновки
«адача компоновки рассматриваетс€ как задача распределени€ принципиальной электрической схемы по платам издели€ и далее по корпусам микросхем. «адачи компоновки могут касатьс€ компоновки микросхем, плат и блоков устройств. ¬ этом случае говор€т о компоновке ћ‘ i-го уровн€ модул€ми i-1-го уровн€.
«адачи компоновки основываютс€ на р€де показателей, по которым оцениваетс€ качество компоновки. ѕоэтому формально задачу компоновки можно сформулировать следующим образом: объединить модули низшего и i-1-го уровн€ в модули более высокого i-го уровн€ по заданным качествам при наличии ограничени€.
—реди методов компоновки выдел€ют 2 разновидности:
1. ћетоды, которые осуществл€ют разбиение коммутационной схемы на части (блоки) с учетом таких ограничений как: число элементов в блоке, число внешних выводов блока и суммарна€ площадь, занимаема€ элементами и соединени€ми.
ќсновными показател€ми качества такого разбиени€ €вл€ютс€:
Ј число образующихс€ блоков,
Ј число межблочных соединений,
Ј величина задержки при распространении сигнала,
Ј электрическа€ магнитна€ и теплова€ совместимость элементов
«адачи такого вида возникают при разбиении коммутационной схемы на блоки, к которым не предъ€влены требовани€ схемной унификации. Ёта задача распределени€ плат по панел€м, интегральных микросхем по платам и коммутационных схем по кристаллам интегральных микросхем. “аким образом, к первой разновидности задач компоновки относ€т такие, в которых критерии качества и ограничени€ могут быть сведены к определенным конструктивным параметрам, характеризующих распределение отдельных элементов и соответствующих межсоединений. Ёти задачи компоновки называют задачами компоновки конструктивных модулей или блоков.
2. ћетоды, в которых кроме конструктивных характеристик модулей важны и их функциональные характеристики. Ёти методы примен€ют на этапе перехода от принципиальных электрических схем к функционально-логическим схемам, ориентированным на заданную систему элементов и эти методы свод€тс€ к назначению элементов логической схемы в типовые модули из заданного набора. ƒанный тип задач основан на методах покрыти€ функционально-логических и принципиальных электрических схем элементами заданной серии и на методах компоновки типовых блоков. ќсновными критери€ми при покрытии схем €вл€ютс€:
|
|
|
Ј число модулей, необходимых дл€ покрыти€ исходной схемы,
Ј число межмодульных соединений,
Ј число типов используемых модулей,
Ј число используемых элементов в модуле (минимизаци€ числа неиспользуемых элементов в модуле)
¬тора€ разновидность примен€етс€ изделий, выпускаемых большими сери€ми и дл€ типовых плат. ≈сли речь идет о заказной Ѕ»—, то анализируетс€ необходимое число элементов на кристалле. ≈сли речь идет о полузаказной Ѕ»— (матрична€ Ѕ»—), то минимизируетс€ избыточность кристалла. ак ограничение выступают конструктивно-функциональные характеристики типовых модулей:
Ц максимально допустимое число элементов i+1-го уровн€ в модул€х i-го уровн€;
Ц максимальное число выводов модул€ i-го уровн€;
Ц ограничение на совместную работу модул€ i-го уровн€.
ƒл€ методов второго типа тоже могут учитыватьс€ конструктивно-технологичесие характеристики нар€ду с функциональными характеристиками. ƒл€ указанных разновидностей задач компоновки выдел€ют алгоритмы компоновки конструктивных и типовых блоков.
1.2. јлгоритмы компоновки

јлгоритмы компоновки классифицируютс€ по критерию, по ограничению на формирование частей или по структуре вычислительной процедуры. — этой точки зрени€ их дел€т на: последовательные, параллельно-последовательные и итерационные.
¬ последовательных алгоритмах вводитс€ последовательный процесс компоновки частей, на каждом шаге которого в очередную часть добавл€етс€ один из элементов, выбираемый по определенному приоритету.
¬ параллельно-последовательных алгоритмах сначала выдел€етс€ некоторое исходное множество групп элементов, которое затем распредел€етс€ по част€м с учетом заданных критериев и ограничений на компоновку. ќбычно эти алгоритмы используют при решении задач компоновки со специальными требовани€ми (например, минимизаци€ числа однотипных блоков) и обладают достаточно сложной структурой. ак правило, алгоритмы этих двух типов примен€ютс€ дл€ создани€ базового (или начального) варианта компоновки. »терационные алгоритмы служат дл€ улучшени€ некоторого начального варианта компоновки в соответствии с прин€тым критерием. ѕри использовании итерационных алгоритмов сначала граф схемы разбивают на определенное число частей произвольным образом. Ќапример, с помощью последовательных алгоритмов, затем по некоторым правилам производитс€ перестановка вершин из одной части графа в другую с целью минимизации числа внешних ребер.
¬ алгоритмах разбиени€, основанных на математических методах, в основном используетс€ метод ветвей и границ и решаетс€ задача о назначении. јлгоритмы разбиени€ с применением метода ветвей и границ состоит из следующих этапов. —начала определ€етс€ нижн€€ оценка разбиени€ графа на заданное число частей. «атем производитс€ построение дерева решений и осуществл€етс€ поиск оптимального результата. «адачу разбиени€ графа схемы на части можно свести к задаче о назначении. ѕри этом ищетс€ вариант назначени€ кандидатов (вершин графа) во все части, дающий минимальные суммарные затраты. ѕри этом кажда€ вершина графа может быть назначена только в одну часть, и в каждой части должны содержатьс€ различные вершины.
|
|
|
јлгоритмы компоновки типовых блоков свод€тс€ к так называемым задачам покрыти€ и типизации. ѕод покрытием понимаетс€ представление функциональной схемы устройства типовыми и конструктивными элементами и св€з€ми между ними с выполнением заданных конструктивных ограничений. ѕри покрытии выдел€ют задачи с несв€занными элементами и функциональными €чейками. ¬ первом случае решают задачи определени€ необходимого числа €чеек дл€ покрыти€ схемы с минимальной суммарной стоимостью и минимизацией числа св€зей между €чейками. ¬о втором случае решают задачу покрыти€ схемы заданным классом функциональных €чеек с минимизацией числа €чеек и суммарного числа св€зей между €чейками.
“ипизаци€ Ц разбиение схемы на части по критерию оптимальности Ц минимум номенклатуры частей разбиени€ или по критерию максимума однотипности используемых €чеек.
1.3. ѕоследовательный алгоритм разбиени€ графа  на
на  кусков
кусков  с учетом запрещенных вершин
с учетом запрещенных вершин
«амечание. Ќекоторые вершины графа жестко закрепл€ютс€ за определенными кусками, причем в каждом куске должно находитьс€ не более одной запрещенной вершины. ќбозначим  Ц множество запрещенных вершин.
Ц множество запрещенных вершин.
„исло вершин в каждом куске равно  .
.
јлгоритм.
1. ¬ычисл€ем матрицу смежности  .
.
2. ¬ыдел€ем первую запрещенную вершину  из
из  и помещаем ее в первый кусок
и помещаем ее в первый кусок  . —оставл€ем список
. —оставл€ем список  вершин, смежных
вершин, смежных  .
.
3. ƒл€ вершин  определ€ем относительные веса
определ€ем относительные веса
 ,
,
где  Ц локальна€ степень вершины
Ц локальна€ степень вершины  ,
,

 Ц число ребер, соедин€ющих вершину
Ц число ребер, соедин€ющих вершину  с вершинами
с вершинами  , вошедшими
, вошедшими  .
.
4. ¬ыбираем вершину  , дл€ которой
, дл€ которой

≈сли таких вершин несколько, то выбираем вершину с большей локальной степенью  .
.
5. ѕолученную вершину  , помещаем в кусок
, помещаем в кусок  .
.
6. ѕодсчитываем число  вершин в куске
вершин в куске  . ≈сли
. ≈сли 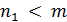 , где
, где  Ц заданное число вершин в каждом куске, то переход к п.8.
Ц заданное число вершин в каждом куске, то переход к п.8.
7. ≈сли  кусок
кусок  сформирован, то переход к п.9.
сформирован, то переход к п.9.
8. ƒобавл€ем в список  вершины, смежные вершинам, вошедшим в кусок
вершины, смежные вершинам, вошедшим в кусок  . ѕереход к п.3.
. ѕереход к п.3.
9. ”дал€ем из матрицы  строки и столбцы, соответствующие номерам вершин, вошедших в кусок
строки и столбцы, соответствующие номерам вершин, вошедших в кусок  . ƒл€ формировани€ следующего куска
. ƒл€ формировани€ следующего куска  , начина€ со следующей запрещенной вершины, процедура повтор€етс€ с п.2. ≈сли сформирован последний кусок, переход к п.10.
, начина€ со следующей запрещенной вершины, процедура повтор€етс€ с п.2. ≈сли сформирован последний кусок, переход к п.10.
10. онец работы алгоритма.
II раздел. ѕрактическа€ часть
ѕостановка задачи
ƒано:
1. —хема соединени€ элементов
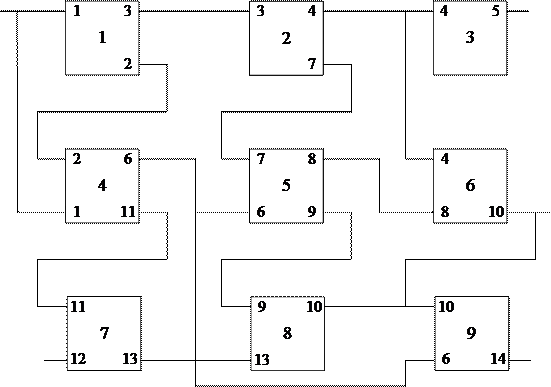 |
2. „исло элементов 
3. „исло кусков разбиени€ 
4. „исло элементов в каждом куске 
5. —писок запрещенных вершин 
“ребуетс€:
1. ѕровести компоновку 3 блоков данной схемы, использу€ ѕоследовательный алгоритм разбиени€ графа схемы  на
на  кусков
кусков  с учетом запрещенных вершин. ¬ычислить число внешних св€зей между блоками.
с учетом запрещенных вершин. ¬ычислить число внешних св€зей между блоками.
2. Ќаписать программу, реализующую данный алгоритм.






