Химически чистые полупроводники называют собственными или полупроводниками i-типа (от intrinsic – внутренний, присущий). Символ i используется в качестве индекса для обозначения параметров собственного полупроводника. Часто используются такие полупроводники как германий, кремний, арсенид галлия и др.
Ширина запрещенной зоны химически чистого германия (четвертая группа Периодической системы) составляет 0,72эВ, у кремния запрещенная зона шире – 1,12эВ. При температуре 0К (абсолютный нуль) ни один электрон валентной зоны не может перейти в зону проводимости. В этом случае германий и кремний являются диэлектриками. Но при повышении температуры полупроводника энергия его валентных электронов возрастает, растет и вероятность их перехода в зону проводимости. При этом надо иметь в виду, что электрон может остаться в том же микрообъеме, в котором и был, т.е. речь идет о переходе на новый уровень энергии, о переходе в энергетическом, а не в пространственном смысле слова. При температуре вещества много большей абсолютного нуля появляются несвязанные, – а значит подвижные – носители заряда, которые появились вследствие теплового возбуждения через запрещенную зону. Например, в обычных условиях, под которыми будем понимать условия эксплуатации электронной аппаратуры, при комнатной температуре 300К проводимость химически чистого кремния составляет 2,0 . 10 -3 См/м, германия – 2,1См/м, тогда как проводимость меди – 5,6 . 10 7 См/м. Данный пример показывает, что в обычных условиях проводимость собственных полупроводников отлична от нуля. При указанной выше температуре их концентрация у германия составляет 10 19 м -3, а у кремния 10 16 м -3. Если учесть, что концентрация атомов в одном м 3 вещества полупроводника порядка 10 28, то в германии число подвижных носителей по отношению к числу атомов составит 10 -7 %, а в кремнии – 10 - 10 %. У металлов же число электронов проводимости не меньше числа атомов, т.е. минимум 100%.
Если произошло тепловое возбуждение валентного электрона в зону проводимости, следовательно, валентная связь оказалась разорванной, а в зоне проводимости появился свободный электрон – носитель заряда. Атом, лишившись электрона, превращается в положительно заряженный ион. Ион локализован, т.е. находится в определенном месте (от лат. locus – место), а именно - в узле кристаллической решетки. Вследствие разрыва валентной связи в валентной зоне появляется вакантный энергетический уровень, т.е. валентная зона оказывается заполненной не полностью, а значит,- создаются условия для появления подвижных носителей и электрического тока. Речь идет о том, что поле иона, в соответствии с законом Кулона, может инициировать процесс перехода электрона из внешней оболочки другого атома на вакантный уровень иона и, как следствие, заполнения вакантной его валентной связи. Наиболее вероятен этот процесс для валентного электрона соседнего атома (валентные электроны, как известно, имеют самую высокую энергию и самую слабую связь с ядром). Соседний атом наиболее близок к рассматриваемому иону, а известно, что сила взаимодействия двух зарядов, в соответствии с законом Кулона, обратно пропорциональна квадрату расстояния между ними. Вследствие этого перехода ион становится нейтральным атомом, а соседний атом превращается в ион. Теперь уже его соседний атом может отдать ему свой валентный электрон и так далее. При отсутствии внешнего электрического поля этот процесс носит пространственно-хаотичный характер, и суммарный импульс подвижных электронов равен нулю. Иными словами, их движение носит беспорядочный, ненаправленный характер.
Наложение внешнего электрического поля увеличивает число электронов, имеющих импульс, направленный вдоль вектора силы, действующей на электроны. Увеличение импульса электронов вдоль какого-либо направления связано с возрастанием их энергии и переходом на более высокие энергетические уровни. При своем движении электроны взаимодействуют (сталкиваются) с атомами. Средняя длина их пробега (называемого свободным) между столкновениями составляет величину порядка 10 -8 м. Следовательно, в поле с напряженностью 10 4 В/м, которая имеет место в кристаллах реальных полупроводниковых приборов при приложении напряжения в несколько вольт, электрон приобретает энергию порядка 10 - 4 эВ, которой явно недостаточно для преодоления запрещенной зоны (табл.1).
Отсюда следует, что электрическое поле заставляет электроны перемещаться направленно, не покидая при этом валентной зоны. Характер их движения можно выразить следующим образом: «от своего атома к соседнему иону в направлении вектора силы». При этом, невзирая на то, что атомы локализованы в узлах решетки, создается впечатление, что происходит движение положительных зарядов (положительных, потому что уход отрицательно заряженного электрона со своего «места» в парноэлектронной связи эквивалентен появлению в нем положительно заряженной частицы) в направлении, обратном направлению движения электронов. То есть вакантная валентная связь как бы перемещается в обратном направлении. Сказанное можно иллюстрировать следующим примером. Представим ряд кресел в зрительном зале. Все кресла, кроме крайнего, заняты зрителями. Зритель, сидящий рядом с пустым креслом, решил на него пересесть, в результате освободилось второе от края место, Если его примеру последуют все остальные зрители, то свободное место будет перемещаться в направлении, противоположном направлению перемещения зрителей, притом, что все кресла (атомы) неподвижны (локализованы). Учитывая изложенное, было принято решение считать незаполненную валентную связь или вакантный энергетический уровень в валентной зоне квазичастицей (как бы частицей), имеющей положительный заряд величиной как у электрона и близкую по величине эффективную массу (об эффективной массе в [2,§54]). Эту частицу назвали дыркой. Действительно, дырка ведет себя как положительный заряд, перемещаясь в направлении вектора напряженности поля. Разумеется, дырка – это абстракция, на самом деле электрический ток в полупроводниках представляет собой направленное движение только электронов. Вместе с тем, введение понятия дырки позволило существенно упростить понимание процессов, происходящих в полупроводниках, без искажения их сути.
Таким образом, в обычных условиях в результате теплового возбуждения атомов собственного полупроводника в веществе появляются электроны проводимости и дырки. Обозначим их концентрации n и p соответственно (от negative – отрицательный и positive – положительный). Введем также индекс i для указания на тип полупроводника – химически чистый. Вполне очевидно, что p i = n i, так как возбуждение электрона через запрещенную зону автоматически приводит к появлению дырки в валентной зоне. Поведение указанных носителей носит динамический характер. В данном случае имеется в виду следующее. Известно, что атом пребывает в возбужденном состоянии весьма короткое время – 10 -12 – 10 -8 с. По истечении этого времени он возвращается в основное состояние. Это означает возвращение электрона из зоны проводимости в валентную зону и заполнение вакантной валентной связи какого-либо атома. В результате одновременно исчезают электрон и дырка, а атом становится нейтральной частицей. Данный процесс носит название рекомбинации. Параллельно происходят процессы термического возбуждения других атомов, приводящие к генерации носителей, т. е. к появлениюэлектронов проводимости и дырок в валентной зоне, т.е. электронно-дырочных пар. Процессы генерации электронно-дырочных пар и процессы их рекомбинации происходят непрерывно, причем среднестатистическая концентрация носителей в веществе постоянна, если постоянна температура и нет каких-либо иных энергетических воздействий. Зависимость концентрации носителей заряда от температуры для невырожденного электронного газа (о невырожденном газе в [2,§52-53]) может быть найдена с учетом статистики Максвелла-Больцмана [3]:
(1)
где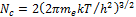 
.
Аналогичные расчеты для дырок дают следующий результат:
, (2)
где 
.
В приведенных выражениях Nc, Nv – эффективные плотности состояний (количество подуровней) в зоне проводимости и валентной зоне соответственно (при комнатной температуре для германия, например, Nc =10 25 м -3, Nv =6∙10 25 м -3 ); me, mh – эффективные массы электрона и дырки (индекс от hole – дыра); h – постоянная Планка; Ec, Ev, Ef – соответственно уровни: «дна» зоны проводимости, «потолка» валентной зоны, Ферми-уровень (уровень максимальной энергии носителя при температуре абсолютного нуля) [2,§51]. В выражениях (1), (2) первый сомножитель оценивает максимально возможное количество носителей заряда, а второй - экспонента – оценивает вероятность термического возбуждения через запрещенную зону. Следует отметить, что с позиции классической физики такое возбуждение невозможно, поскольку тепловая энергия кТ (к - постоянная Больцмана, к=1,38 
10 -23 Дж град -1) составляет при комнатной температуре 300К всего 0,025эВ, при том, что ширина запрещенной зоны германия, например, 0,72эВ. В соответствии же с квантовой физикой вероятность такого перехода больше нуля, что и подтверждается экспериментом.
В равновесном состоянии собственного полупроводника концентрации электронов в зоне проводимости и дырок в валентной зоне равны, т.е. ni=p i, что очевидно, поскольку возбуждение электрона автоматически приводит к появлению дырки в валентной зоне. Следовательно, приравнивая (1) и (2), можно получить выражение для уровня Ферми:
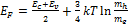. (3)
Как следует из полученного выражения, при Т=0 
, (4)
т.е. при температуре абсолютного нуля уровень Ферми располагается в середине запрещенной зоны (рис. 7б). При более высоких температурах он сдвигается вверх, но так как второе слагаемое (3) существенно меньше первого, то этот сдвиг незначителен.
Поскольку при возбуждении электрона одновременно появляется и дырка, то полагают, что на возбуждение каждого из носителей нужно затратить энергии не менее ∆ 
Отсюда 2kT является характерным параметром в законах распределения носителей по их энергиям. Энергетические диаграммы собственного полупроводника приведены на рис. 7.
Рис.7 Схема электронных уровней собственного полупроводника:
а) – собственный полупроводник при температуре абсолютного нуля ведет себя как диэлектрик; б) – собственный полупроводник, в котором электроны термически возбуждаются через запрещенную зону.Значками «+» и «-» обозначены дырки и электроны соответственно.Распределение концентраций электронов и дырок на рисунке показано справа.
За время жизни носителей, под которым в известной степени можно понимать интервал времени от момента генерации носителей до момента их рекомбинации, они, в отсутствии поля, пребывают в беспорядочном движении теплового характера. Однако, если электроны принадлежат всему кристаллу и обладают свободой передвижения в любом направлении, определяемым вектором силы, то дырки в некоторой степени ограничены, так как могут перемещаться лишь от одного соседнего атома к другому. Для количественной оценки различия в характере движения частиц, был введен параметр, названный подвижностью и обозначаемый символом 
. Подвижность представляет собой удельную - на единицу напряженности внешнего электрического поля – среднюю скорость носителей:
, [м 2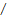 
(В . c)]. (5)
Подвижность дырок у собственного германия составляет 0,17, а у электронов 0,36м 2 /(В . с). То обстоятельство, что дырки обладают меньшей подвижностью, чем электроны, объясняется тем, что на их движение накладывается ограничение, указанное выше: их перемещение возможно только от данного атома к соседнему. Для электронов такого ограничения не существует, поскольку, покинув свой атом, они принадлежат всему кристаллу. Следовательно, при наложении электрического поля электроны движутся прямолинейно (без учета хаотичного движения теплового характера) в направлении вектора силы. Направление движения дырок также определяется полем, но путь их не прямолинеен, а соответствует характеру пространственного размещения атомов в кристаллической решетке, т.е. более «извилист».
Проводимость, имеющая размерность 1 / (Ом 
м) и обусловленная свободными носителями, находящимися в единице объема вещества, равна произведению суммарного их заряда (в Кл/м3) на величину их подвижности. В свою очередь, полный заряд единицы объема вещества полупроводника равен произведению концентрации носителей (в м-3) на заряд электрона. Таким образом, проводимость собственного полупроводника с учетом подвижности обоих видов носителей найдется:
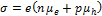(6)
или, учитывая, что у собственных полупроводников ni=pi=n,
(7)
В случае с примесными полупроводниками, например электронными, концентрацией дырок можно пренебречь. Тогда проводимость найдется как 
Проверка размерности проводимости правой части последнего выражения дает следующий результат: 
Поскольку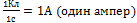 
, а количество электронов в единице объема размерности не имеет и приведено лишь для понимания методики расчета, получаем в итоге А/(В٠м), т.е См / м.
. Влияние дефектов кристаллической решетки
Реальные вещества кристаллической структуры, включая полупроводники, не имеют идеально правильного расположения атомов, молекул или ионов. У них всегда имеются так называемые дефекты - отклонения от строгой упорядоченности кристаллической решетки. Существует большое количество дефектов, классифицируемых по геометрическим признакам на точечные, линейные (одномерные), поверхностные (двухмерные) и объемные (трехмерные).
Точечные дефекты имеют малую (порядка нескольких атомных размеров) протяженность в любом направлении. К ним относят вакансии – отсутствие атомов в некоторых узлах решетки и наличие атомов в междоузлиях (рис.8 а,б).
а) б) в) г)
Рис.8. Точечные дефекты кристаллической решетки
Указанные дефекты могут возникнуть, например, при усилении тепловых колебаний атомов с ростом температуры или при облучении вещества потоком частиц. При этом атом решетки может покинуть узел и внедрится в междоузлие в другой части кристалла (атом внедрения). Атом внедрения и образовавшаяся одновременно вакансия являются подвижными дефектами и могут перемещаться по кристаллу. Так, место вакансии может занять атом из соседнего узла, а вакансия сместиться на его место. Если плотность упаковки атомов невелика, то вокруг атомов внедрения решетка деформируется. У веществ с плотной упаковкой атомов (например, меди, цинка) образование подобных дефектов маловероятно.
Атомы внедрения могут появляться за счет примеси посторонних веществ, которые неизбежно присутствуют в исходном полупроводнике даже при самой тщательной его очистке. Наличие такой неконтролируемой примеси вызывает появление нежелательных свойств полупроводника. Для очистки вещества от примесей используют сложные технологии (например, метод Чохральского), однако полностью избавиться от них практически невозможно. Вместе с тем, примеси зачастую вводят специально для придания веществу (примесному полупроводнику) необходимых свойств. Введение такой (контролируемой) примеси называют легированием. Примесные атомы могут также занимать места вакансий и располагаться в узлах решетки (атомы замещения, рис. 8г). Концентрация примесных атомов может быть различной. В чистом германии она составляет примерно 10 18 м -3, в легированном (обогащенном примесями) германии 10 20 – 10 24 м -3. В некоторых полупроводниковых приборах и приборах квантовой электроники концентрацию примеси доводят до величин, соответствующих предельной растворимости в полупроводнике – до 10 27 м -3. 
Поверхностными дефектами являются поверхность кристалла, границы зерен (если вещество получено, например, прессованием или спеканием тонко измельченного материала) и т.д. Поверхность кристалла ограничивает решетку с одной стороны, и поверхностные атомы уже не окружены со всех сторон другими атомами, как это имеет место в объеме кристалла. В этом случае нарушается симметрия связей и, следовательно, изменяется поведение атомов.
К объемным дефектам относят пустоты, трещины, поры, включения нерастворимых примесей. В общем случае к дефектам относят и тепловые колебания атомов решетки, при которых атомы смещаются относительно своего положения равновесия. Дефекты структуры оказывают существенное влияние на механические, тепловые, электрические, магнитные и оптические свойства твердых тел.
Таким образом, химически чистыми вещества можно называть лишь условно.
Наличие дефектов кристаллической структуры искажает поле решетки и, как следствие, приводит к появлению разрешенных энергетических уровней в запрещенной зоне, в частности, вблизи «потолка» валентной зоны и «дна» зоны проводимости, имея энергетический «зазор» между ними порядка kТ. Как следствие, велика вероятность того, что электрон, находящийся в зоне проводимости, будет захвачен уровнем дефекта, а затем вследствие тепловых колебаний решетки, получив от нее энергию порядка kT, вновь вернется в зону проводимости. Подобная ситуация может повторяться многократно. Поэтому уровни дефектов называют уровнями ловушек или просто ловушками. Они могут располагаться в любом месте запрещенной зоны. Благодаря ловушкам, расположенным вблизи зоны проводимости, пребывание электронов в зоне проводимости может существенно превысить время возбужденного состояния (время жизни носителя), в результате чего концентрация свободных электронов в веществе увеличивается. Наличие ловушек вблизи валентной зоны приводит к аналогичным явлениям для дырок.
Примесная проводимость полупроводников
Помимо химически чистых веществ, широкое применение находят полупроводники, легированные различного рода примесями. Легирование (целенаправленное введение примесей) может осуществляться, например, способом высокотемпературной диффузии из газовой фазы. Как следствие, в решетке чистого полупроводника появляются атомы внедрения, замещающие собственные его атомы, что вызывает появление, в свою очередь, разрешенных энергетических (примесных)уровней в запрещенной зоне. Если, например, осуществить легирование германия мышьяком, то замещение одного из атомов четырехвалентного германия атомом пятивалентного мышьяка приведет к тому, что пятый электрон примесного атома не будет участвовать в установлении ковалентной связи. Он будет перемещаться по эллиптической орбите вокруг иона примеси, охватывая своим движением несколько атомов решетки (на самом деле никаких орбит, как таковых, не существует, правильнее сказать – в окрестности иона; понятие орбиты используют в целях наглядности). Такой электрон из-за своей удалённости слабо связан со своим атомом. И теперь достаточно сообщить ему энергию порядка 0,01эВ, чтобы оторвать его от атома и превратить в свободный электрон, увеличивающий проводимость кристалла. Таким образом, с точки зрения зонной теории атому мышьяка соответствует появление локального энергетического уровня, расположенного в запрещенной зоне примерно на 0,01эВ ниже дна зоны проводимости. Примесные уровни мышьяка заполнены электронами, которые под действием внешнего возбуждения относительно легко могут перейти в зону проводимости. Так, при температуре 27 0 C (300К) тепловая энергия составляет 0,025эВ, следовательно, в обычных условиях, при комнатной температуре, все атомы примеси ионизованы, а их валентные электроны имеют энергию, соответствующую зоне проводимости. Следует отметить, что появление такого свободного электрона не сопровождается нарушением ковалентной связи, т.е. образованием дырки. Хотя в окрестности атома примеси и возникает избыточный положительный заряд, но он локализован в узле решетки и перемещаться по ней не может. И, поскольку валентные связи с соседними атомами основного полупроводника заполнены, он не может принять электрон соседнего атома, несмотря на наличие сил притяжение в соответствии с законом Кулона.
Совершенно очевидно, что в данном случае условие ni= n p нарушается, и концентрация электронов проводимости на многие порядки становится выше концентрации дырок. Такие примесные уровни, передающие электроны в зону проводимости, называются донорными (дающими), а соответствующие атомы примеси – донорами. Поскольку концентрация электронов проводимости на порядки превышает концентрацию дырок, то электроны считают основными носителями, а дырки – неосновными. Вследствие этого подобные примесные полупроводники называют полупроводниками n -типа или донорными. Все параметры донорного полупроводника имеют индекс n, следовательно, указанное неравенство концентраций носителей записывается n n >> p n.
Поскольку введение примеси приводит к резкому увеличению концентрации носителей заряда – основных электронов, то проводимость полупроводника также резко возрастает, причем, в данном случае она имеет электронный характер.
При введении в решетку германия атомов трехвалентного вещества, например, индия, три его валентных электрона не могут обеспечить ковалентные связи с четырьмя атомами германия, и одна из связей остается незаполненной. Её нельзя считать дыркой поскольку она не является вакансией, и атом примеси остается электрически нейтральным. Вследствие тепловых флуктуаций эту связь может заполнить валентный электрон соседнего атома германия. В результате достройки ковалентной связи, в окрестности атома примеси возникнет избыточный отрицательный заряд, поскольку заряд его ядра по модулю меньше заряда электронов, находящихся в окрестности атома примеси. Но этот заряд будет связан с данным атомом (локализован) и не может стать носителем тока. В то же время уход валентного электрона от атома основного полупроводника приводит к образованию реальной вакансии валентной связи у атома германия. Т.е. появляется дырка, которая может быть заполнена электроном соседнего основного атома, та, в свою очередь другого соседнего и так далее. Следовательно, вакансия электрона подвижна и может перемещаться вдоль решетки. Эти перемещения носят хаотичный характер и среднее значение импульса электронов, переходящих от одной незаполненной связи к другой, равно нулю. Но, при наложении электрического поля перемещение носителей станет ориентированным в соответствии с направлением вектора силы, т.е. возникнет электрический ток, формально являющийся дырочным.
Данная ситуация эквивалентна появлению в запрещенной зоне локальных незаполненных энергетических уровней на расстоянии примерно 0,01эВ от потолка валентной зоны, на которые могут перейти электроны валентной зоны под действием внешнего возбуждения. В результате такого перехода валентная зона оказывается не полностью заполненной, в ней образуются дырки, обеспечивающие механизм электропроводности. Подобные примесные уровни, на которые могут переходить электроны валентной зоны, называются акцепторными (от англ. accept – принимать), а соответствующие атомы примеси – акцепторами. Поскольку энергетический «зазор» между акцепторными уровнями и зоной проводимости остается достаточно большим – порядка 0,1 – 1,0эВ, то введение акцепторной примеси практически не вызывает изменения концентрации электронов проводимости Она даже несколько уменьшается, так как рост концентрации дырок увеличивает вероятность процессов рекомбинации. В то же время, поскольку в обычных условиях, при комнатной температуре, практически все примесные уровни оказываются заполненными электронами, перешедшими из валентной зоны, концентрация дырок резко возрастает, и они становятся основными носителями, а электроны – неосновными. Подобные примесные полупроводники называют полупроводниками p -типа, а атомы примеси – акцепторами. Параметры акцепторного полупроводника имеют индекс p, отсюда p p >>n p.
Как видим, введение акцепторной примеси тоже резко увеличивает проводимость вещества, только в этом случае она имеет дырочный характер. Вполне понятно, что электрический ток и в этом случае представляет собой поток электронов, которые под действием поля перемещаются по кристаллу, заполняя одну вакансию за другой. Но, если бы эти вакансии отсутствовали, т.е. если бы валентная зона оказалась полностью заполненной, то наложение поля не привело бы к появлению электрического тока, поскольку отсутствовали бы своеобразные «посадочные места» в виде незаполненных валентных связей или вакантных энергетически уровней в валентной зоне.
Энергетическая диаграмма примесного полупроводника приведена на рис. 9. Ионы акцепторов и доноров обозначены как 
, подвижные носители – электроны и дырки как «_» и «+» соответственно.
Рис.7.5. Диаграмма энергии электронов для примесных полупроводников:
а – полупроводник n -типа, в котором почти все донорные примеси ионизированы;
б - полупроводник p -типа, в котором почти все акцепторные уровни заняты электронами, возбуждаемыми из валентной зоны.
Примесные уровни и уровни ловушек могут быть весьма близко расположены друг к другу. Однако их роли существенно отличаются: появление первых приводит к росту проводимости p и n типов, вторые увеличивают время возбужденных состояний, что, в конечном счете, также приводит к росту концентрации носителей, но одновременно увеличивается и инерционность фотоприемника, в котором используется такой кристалл. Совершенно очевидно, что если ставится задача контролируемого увеличения проводимости полупроводника, то вещества примеси специально подбирают таким образом, чтобы получить разрешенные уровни вблизи валентной зоны и зоны проводимости. Это означает, что в обычных условиях, при комнатной температуре, все примесные центры оказываются ионизированными и проводимость кристалла возрастает. При повышении температуры концентрация примесных центров может достигнуть насыщения. Это означает, что освобождаются (от валентных электронов) практически все донорные или заполняются электронами (из валентной зоны) все акцепторные уровни. Одновременно растет и собственная проводимость полупроводника, обусловленная переходом электронов непосредственно из валентной зоны в зону проводимости. Следовательно, проводимость примесного полупроводника будет складываться из примесной и собственной проводимостей. При низкой температуре вещества будет преобладать примесная проводимость, а при высокой (при условии насыщения примесных центров) – собственная проводимость.
Представление о порядке величин числа примесных атомов дают следующие цифры: число атомов германия 5 . 10 28 м -3, число примесных атомов 5 . 10 20 м -3. Следовательно, их соотношение примерно 1:10 8. В табл.2 приведена информация о положении донорных и акцепторных уровней двух полупроводников – германия и кремния с различными добавками, а табл.3 содержит характеристики наиболее важных полупроводниковых материалов.
место для таблиц
Для понимания дальнейшего материала необходимо представить себе следующее. Когда электрон покидает атом – донор, возбуждаясь в зону проводимости, то донор, бывший ранее нейтральной частицей, приобретает некомпенсированный заряд, равный заряду электрона, т.е. становится положительным ионом. Атом – акцептор при достройке ковалентной связи принимает лишний электрон (уход которого от атома собственного полупроводника приводит к появлению дырки) и также становится ионом, но имеющем отрицательный заряд, равный заряду электрона. Ионы примеси в обычных условиях неподвижны, в том смысле, что располагаются в узлах кристаллической решетки, совершая колебания теплового характера относительно положения равновесия. Свободные электроны и дырки напротив подвижны, их движение в отсутствие поля хаотично и носит тепловой характер, а при наложении поля становится упорядоченным (но тепловой характер движения остается как компонент).
В случае однородного кристалла рассмотренные эффекты (появление некомпенсированных зарядов) проявляются только локально, в масштабе порядка атомных размеров, а в большом объеме, с большим количеством доноров или акцепторов, результирующая плотность объемного пространственного заряда равна нулю (сколько положительных зарядов, столько и отрицательных) и кристалл в целом электрически нейтрален.
Список условных обозначений, сокращений и терминов
ЭМИ – электромагнитное излучение.
ЭМВ – электромагнитная волна.
ЧЭ – чувствительный элемент фотоприемника – часть поверхности его кристалла, на которую падает поток излучения.
Флуктуация - отклонение от среднего значения какой-либо физической величины, имеющее случайный характер.
Атомная частица – частица микромира: молекула, атом, ион, электрон и т.д.
Библиографический список
Савельев И.В. Курс общей физики. т.2. Электричество и магнетизм. Волны. Оптика.- М.: «Наука», 1978, 480с.-ил.
Савельев И.В. Курс общей физики. т.3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц.- М.: «Наука», 1979, 304с.-ил.
Трофимова Т.И. Курс физики. Учеб. пособие для втузов.-М.: «Высшая школа», 2000, 542с.-ил.
Фридрихов С.А., Мовнин С.М. Физические основы электронной техники: Учеб. для вузов.- М.: Высшая школа, 1982.- 608с.
Киреев П.С. Физика полупроводников. Учеб. пособие для вузов.-М.: Высш. шк., 1969,- 592с.
Щука.Электроника.
Пихтин А.Н. Оптическая и квантовая электроника: Учеб. для вузов.- М.: Высш. шк., 2001.-573с.
Павлов А.В., Черников А.И. Приемники излучения автоматических оптико-электронных приборов.- М.: Энергия, 1972.- 240с.
Василевский А.М. и др. Оптическая электроника.- Л.: Энергоатомиздат, 1990.- 176с.
Носов Ю.Р. Дебют оптоэлектроники.- М.: Наука, 1992.-240с.-(Б- чка «Квант», вып.84)
