t = V: UA, (3.22)
де V – реакційний об’єм; UA – об’ємна витрата реакційної суміші.
Математична модель (характеристичне рівняння) для РІВ виводиться на підставі матеріального балансу для елементарного об’єму реактора.
 |
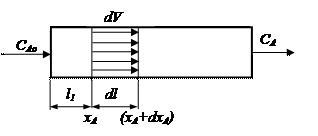Рис. 3.4. До складання матеріального балансу РІВ
Нехай у РІВ відбувається реакція А® R. Виділимо всередині реактора деякий елементарний об’єм dV, обмежений стінками реактора і поперечними перерізами, які розміщені на віддалі dl (рис. 3.4).
Нехай реакційна суміш проходить від входу в реактор до виділеного об’єму відстань l1. За цей час (t1) досягається ступінь перетворення хА. За час проходження виділеного об’єму завдовжки dl приріст ступеня перетворення становить dxA. Отже, на виході із елементарного об’єму сумарне значення ступеня перетворення дорівнює (xA + dxA).
У реактор входить реаґент А кількістю
GA.прих = UACAo. (2.23)
За час t1 кількість прореагованої речовини А дорівнює
GA.прореаг = UACAoхА. (3.24)
Отже, на вході в елементарний об’єм кількість реаґенту становить
GА, прих = UAСАо(1 - хА). (3.25)
В елементарному об’ємі реагує речовина А кількістю
dGA.прореаг = UACAo(хА + dxA). (3.26)
Тоді на виході з цього об’єму кількість реаґенту дорівнює
dGA.вих = UACAo(1 – (хА + dxA)). (2.27)
Загалом, на виході із зазначеного об’єму витрата реаґенту становить
GА, витр = GA,вих + GA,х.р. = UA САо(1-(хА + dxA)) + uАdV, (2.28)
де xA – ступінь перетворення реаґенту А за час проходження реаґентом відстані від входу в реактор до елементарного об’єму; dxA – приріст ступеня перетворення, який досягається в елементарному об’ємі реактора; uА – швидкість хімічного перетворення реаґенту А; dV – елементарний об’єм реактора.
Прирівнявши рівняння (3.25) і (2.28), отримаємо
UA САо dxA = uАdV. (3.29)
Розв’яжемо це рівняння щодо t – часу перебування реаґенту А в реакторі
, (3.30)
звідки
. (3.31)
Отриманий вираз – це характеристичне рівняння для РІВ, записане у загальному вигляді.
Для простої необоротної реакцій А®R нульового порядку швидкість, згідно із законом діючих мас, дорівнює
Звідки час перебування в реакторі становить
. (3.32)
Для простої необоротної реакцій А® R першого порядку швидкість дорівнює
. (3.33)
Підставивши цей вираз у рівняння (3.31), отримаємо
. (3.34)
Відтак характеристичне рівняння РІВ для реакцій першого порядку має вигляд
. (3.35)
Як видно із цього рівняння, значення початкової концентрації не впливає на час перебування реаґентів у реакторі, який необхідний для досягнення заданого ступеня перетворення.
Для простої необоротної реакцій n -го порядку, швидкість якої дорівнює
, (3.36)
час перебування у реакторі становить
. (3.37)
Розв’язавши цей інтеграл, отримаємо підсумкове характеристичне рівняння для РІВ:
. (3.38)
Для оборотної реакції першого порядку А Û R швидкість дорівнює
, (3.39)
де СА = САо(1 - хА), СR = САохА.
. (3.40)
Отже, час перебування реаґентів у реакторі дорівнює
, (3.41)
звідки 
. (3.42)
Якщо під час перебігу хімічної реакції відбувається зміна об’єму реакційного середовища, то її враховують при виведенні характеристичного рівняння.
Коефіцієнт зміни об’єму дорівнює
, (3.43)
де Vo і Vк – початковий і кінцевий об’єми реакційного середовища в реакторі.
Очевидно, що залежно від того чи реакція відбувається із збільшенням реакційного об’єму, чи зменшенням, значення цього коефіцієнта може бути відповідно більшим або меншим від нуля.
Значення об’єму реакційного середовища залежить від коефіцієнта зміни об’єму та ступеня перетворення, який досягається на певний момент перебігу реакції:
V = Vo + exAVo, (3.44)
де Vo – початковий об’єм реакційного середовища за хА=0; exAVo – зміна об’єму реакційного середовища.
Концентрацію реаґенту А, яка фігурує у характеристичному рівнянні, виразимо через відношення його маси до значення реакційного об’єму в певний момент часу. Маса реаґенту А за ступеня перетворення хА дорівнює
GA = GAo(1 – xA).
Відповідно концентрація реаґенту становить
. (3.45)
Час перебування у реакторі у випадку, коли відбувається зміна реакційного об’єму, для реакцій n- го порядку дорівнює
, (3.46)
звідки
. (3.47)
3.2.2. Реактори ідеального змішування (РІЗ)
Реактори цього типу – це ємнісні апарати, в яких здійснюється дуже інтенсивне перемішування реаґентів. Будь-який елемент об’єму реаґенту, що надходить у реактор, миттєво змішується із реакційною сумішшю, яка вже знаходиться в апараті, бо швидкість циркуляції потоку за висотою та перерізом реактора є значно більшою, ніж швидкість лінійного переміщення вздовж його осі. У цьому випадку ефективний коефіцієнт дифузії D ® ¥, а дифузійний критерій Пекле є мінімальним, Ре ® 0. Унаслідок цього концентрації компонентів реакційної суміші – реаґентів та продуктів, миттєво й рівномірно розподіляються в об’ємі реактора: у будь-який момент часу концентрація речовин є однаковою (але не сталою) у будь-якій точці реакційного об’єму. Відтак і показники процесів (швидкість, ступінь перетворення, селективність тощо), що відбуваються у реакторі, є абсолютно однаковими у кожній точці в певний момент часу.
Наприклад, у певний момент часу tі в усіх точках реактора виконуються такі умови:
CJ(х1, у1, z1, tі) = СJ(х2, у2, z2, tі) =... = СJ(хN, уN, zN, tі);(3.48)
; 
; 
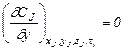; (3.49)
хА(х1, у1, z1, tі) = хА(х2, у2, z2, tі) =... = хА(хN, уN, zN, tі); (3.50)
; 
; 
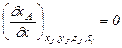, (3.51)
де х, у, z – просторові координати.
Отже, модель РІЗ ґрунтується на допущенні про безградієнтність, тобто відсутність різниці між параметрами середовища та показниками процесу в усьому об’ємі реактора у кожен момент часу. Це можливо лише за ідеальних умов перемішування (чого в реальних реакторах досягнути дуже важко), тому назва моделі таких реакторів – реактор ідеального змішування.
Режим ідеального змішування, а в реальних реакторах режим, що наближується до нього, забезпечується дуже інтенсивним перемішуванням реакційного середовища механічними мішалками, циркуляційними насосами або стисненим повітрям. Тому РІЗ умовно зображаються як ємнісний реактор з мішалкою або значно рідше з циркуляційним насосом чи пневматичним перемішуванням (рис. 3.5).
Рис. 3.5. Схематичне зображення РІЗ: а – з механічною мішалкою;
б – з циркуляційним насосом; в – з пневматичним перемішуванням; 1 – корпус реактора; 2 – мішалка; 3 – циркуляційний насос; 4 – компресор
Хоча у РІЗ, як зазначалось, значення параметрів реакційної суміші (СА, uA, xА) у певний момент часу є однаковими в реакційному просторі, але характер їх зміни під час перебігу хіміко-технолоґічного процесу залежить від характеру роботи реактора в часі.
3.2.2.1. Реактор ідеального змішування періодичної дії (РІЗ-П)
У РІЗ-П хіміко-технолоґічний процес відбувається у замкненій системі: спочатку завантажують вихідні реаґенти, а продукти реакції вивантажують лише після закінчення процесу. Під час реакції жодні речовини в реактор не вводяться і не виводяться із нього. Отже, протікання речовин через реактор під час реакції немає, тому РІЗ-П належить до непроточних реакторів. У зв’язку з цим можна вважати, що лінійна швидкість потоку через реактор дорівнює нулю. Відтак у рівнянні матеріального балансу відсутні гідродинамічні складові, які враховують прихід та витрату речовин з матеріальними потоками (DGАгідр = 0).
За перебігу реакції у закритому об’ємі сумарна маса реакційного середовища у реакторі є сталою, але її якісний і кількісний склад (концентрації реаґентів і продуктів) є змінним і залежить лише від тривалості здійснення процесу. Швидкість процесу у РІЗ-П у часі буде падати, бо зменшуються концентрації реаґентів.
Очевидно, що оскільки швидкість реакції є функцією від концентрації реаґенту, то залежності їх від часу матимуть схожий характер (рис. 3.6,а,б). Відповідно і зміна ступеня перетворення, який також визначається за концентрацією реаґенту у певний момент часу, матиме подібний, але обернений до перших двох параметрів, вигляд (рис. 3.6,в).
 |
Рис. 3.6. Зміна концентрації реаґенту (а), швидкості (б)
та ступеня перетворення (в) в РІЗ-П у часі
Оскільки параметри реакційного середовища (СА, uA, xА) є змінними у часі, то реактор періодичної дії належить до нестаціонарних. Разом з тим у РІЗ-П реалізується режим ідеального перемішування, тому в певний момент часу параметри процесу є однаковими у будь-якій точці реакційного об’єму (рис. 3.7). Реакція у РІЗ-П відбувається у нестаціонарному режимі, тому рівняння матеріального балансу, в якому відсутні гідродинамічні складові, для реакційного об’єму записують у диференціальній формі
. (3.52)
 |
Рис. 3.7. Розподіл концентрації реаґенту А в об’ємі реактора РІЗ-П
у певні моменти часу
Оскільки для реакції А ® R
,
то 
. (3.53)
Розв’яжемо це рівняння відносно часу перебування реаґентів у реакторі
та проінтегруємо його за значеннями часу від нуля до t, за яких значення ступеня перетворення дорівнюють відповідно нулю та хА
. (3.54)
Звідти 
. (3.55)
Отриманий вираз – це характеристичне рівняння РІЗ-П, записане у загальному вигляді.
Для реакції першого порядку час перебування реаґентів у реакторі РІЗ-П дорівнює
. (3.56)
Отже, характеристичне рівняння РІЗ-П для реакцій першого порядку матиме аналогічний вигляд до реактора ідеального витіснення
. (3.57)
Також у випадку простих необоротних реакцій n -го порядку, швидкість яких дорівнює
, (3.58)
час перебування у РІЗ-П визначається за тим самим рівнянням, що й для РІВ
. (3.59)
Час, розрахований за рівняннями (3.57) і (3.59), є “чистим”, тобто необхідним для перебігу лише хімічної реакції. Але здійснення процесу у реакторах періодичної дії потребує додаткових витрат часу на завантаження реаґентів, вивантаження продуктів, а часто ще й на виведення реактора на робочий режим (наприклад, нагрівання до заданої температури). Через це у реакторів періодичної дії зменшується продуктивність роботи, їх складніше автоматизувати.
Використовують РІЗ-П переважно в малотоннажних виробництвах, у гнучких технолоґічних процесах, зокрема, для одержання реактивів і особливо чистих речовин, лікарських препаратів, барвників тощо.
3.2.2.2. Реактори ідеального змішування безперервної дії (РІЗ-Б)
Реактор типу РІЗ-Б належить до відкритих систем, в яких введення вихідних реаґентів і виведення продуктів здійснюється безперервно. Такі реактори належать до проточних апаратів. У РІЗ-Б відбувається різка зміна концентрації реаґенту, який вводиться в реактор, унаслідок миттєвого і повного змішування його з реакційною сумішшю, що вже знаходиться в реакторі і має концентрацію, нижчу, ніж на вході. При цьому концентрація реаґенту вирівнюється в об’ємі реактора (рис. 3.8,а), а рушійна сила процесу хімічної взаємодії (різниця концентрацій) різко зменшується. Відповідно, реакція відбувається лише у момент, коли вводиться свіжий реаґент, і дуже швидко припиняється внаслідок вирівнювання концентрацій реаґентів (рис.3.8,б). Це призводить до того, що ступінь перетворення у РІЗ-Б є невисоким. Характер зміни ступеня перетворення є схожим, але оберненим до зміни концентрації реаґенту та швидкості реакції (рис.3.8,в).
 |
Рис. 3.8. Зміна параметрів процесу в елементарному об’ємі РІЗ-Б: а – концентрації реаґенту; б – швидкості реакції; в – ступеня перетворення
Завдяки постійному введенню свіжого реаґенту та інтенсивному перемішуванню в усьому об’ємі реактора дуже швидко встановлюється однакова концентрація реаґентів та продуктів, швидкість реакції та ступінь перетворення (рис. 3.9). Ці значення зберігаються протягом усієї тривалості роботи реактора за умови, якщо технолоґічні параметри роботи реактора є сталими.
Отже, модель РІЗ-Б у цілому є безградієнтною – градієнт (різниця) параметрів стану і властивостей (СА, uА, xА) реакційного потоку в усьому реакційному об’ємі в будь-який момент часу відсутній. Тому робота такого реактора відбувається у стаціонарному режимі.
 |
Рис. 3.9. Зміна параметрів процесу в РІЗ-Б в часі: а – концентрації реаґенту;
б – швидкості реакції; в – ступеня перетворення
Варто зауважити, що у реальних умовах під час запуску, виходу на режим, зупинки ці реактори працюють у нестаціонарному режимі. Однак зазначені стадії роботи реактора безперервної дії за тривалістю є значно меншими, ніж робота в усталеному режимі.
Оскільки у РІЗ-Б градієнт параметрів відсутній, то матеріальний баланс складається для всього реактора (реакційного об’єму) в інтегральній формі
Gприх = Gвитр, (3.60)
де Gприх – кількість реаґенту А на вході в реактор, Gприх = UACAo; Gвитр – кількість реаґенту А, яка витрачається.
Gвитр = Gх.р + Gвих , (3.61)
де Gх.р – кількість реаґенту А, який прореагував за час перебування в реакторі; Gвих – кількість реаґенту А, який виходить із реактора непрореагованим.
Gх.р = uAVA. (3.62)
Gвих = UACAo – UACAoxA = UACAo(1 – xA). (3.63)
Отже, витрата реаґенту А становить
Gвитр = uAVA + UACAo(1 – xA). (3.64)
Матеріальний баланс для РІЗ-Б має вигляд
UACAo = uAVA + UACAo(1 – xA). (3.65)
Час перебування реаґентів у реакторі t = V/UA, тому останнє рівняння розв’яжемо відносно t й отримаємо характеристичне рівняння для РІЗ-Б, записане в інтегральній формі:
. (3.66)
Для реакцій першого порядку (n = 1) це рівняння набере вигляд
, (3.67)
звідки 
. (3.68)
Як і в попередніх випадках (для реакторів РІВ і РІЗ-П), початкова концентрація реаґентів не впливає на тривалість їх перебування у реакторі, яка необхідна для досягнення заданого ступеня перетворення.
Для реакцій n -го порядку за умови сталості об’єму реакційної суміші час перебування реаґентів у реакторі дорівнює
, (3.69)
або 
. (3.70)
Розглянемо випадок, коли під час хіміко-технолоґічного процесу відбувається зміна реакційного об’єму.
Для реакцій першого порядку, швидкість яких виражається рівнянням
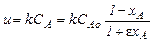, (3.71)
час перебування у реакторі дорівнює
, (3.72)
або 
. (3.73)
Для реакцій n- го порядку характеристичне рівняння має вигляд
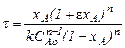. (3.74)
Час t, одержаний із характеристичного рівняння, є усередненим значенням реального часу можливого перебування частинок реаґенту в реакторі. Дійсно, якщо у реактор одночасно вводять потік свіжого реаґенту й виводять потік із продуктом, то в останній буде потрапляти і виводитись з реактора частина реаґенту, який щойно ввійшов. З іншого боку, певна кількість частинок реаґенту може знаходитись у реакторі нескінченно довго. Тобто дійсна тривалість перебування частинок реаґенту може змінюватись від 0 до ¥. Тому час перебування реаґентів у реакторі розглядають як тривалість оновлення вмісту проточного реактора. Цей час зв’язаний з конструктивними характеристиками реактора – його об’ємом і об’ємною витратою реакційної суміші, співвідношенням t = V/UA.
Якщо у РІЗ-Б відбувається оборотна реакція A Û R, то її швидкість визначається із рівняння
.
Тоді час перебування реаґентів у РІЗ-Б дорівнює
, (3.75)
звідки 
. (3.76)
3.2.2.3. Каскад реакторів ідеального змішування безперервної дії (КРІЗ-Б)
Суттєвим недоліком одиничного РІЗ-Б є низький ступінь перетворення. Для його збільшення необхідно забезпечити більшу тривалість перебування реаґентів у реакторі, а з цим зв’язана необхідність застосування реакторів великих об’ємів. Тому збільшити цей час можна, використовуючи декілька однакових послідовно з’єднаних між собою РІЗ-Б, які утворюють каскад КРІЗ-Б (рис.3.10).
При внесенні реаґенту матеріальним потоком у кожен наступний реактор виникає деякий градієнт концентрацій, який миттєво прямує до нуля внаслідок перебігу хімічної реакції. При цьому досягається певний ступінь перетворення вихідного реаґенту. Очевидно, що у кожному наступному реакторі каскаду рушійна сила процесу є меншою, ніж у попередньому, бо концентрація реаґенту зменшується, тому приріст ступеня перетворення у кожному наступному реакторі буде відповідно меншим. Але завдяки тому, що реакторів у каскаді є декілька, сумарна рушійна сила процесу є більшою, ніж в одиничному РІЗ-Б такого самого об’єму. Отже, сумарний ступінь перетворення в КРІЗ-Б є вищим.
 |
Рис. 3.10. Каскад реакторів ідеального змішування безперервної дії: а – принципова схема КРІЗ-Б; б – зміна концентрації реаґенту А (1– в окремих ступенях каскаду; 2 – середня); в – зміна ступеня перетворення
Кількість реакторів у каскаді, яке необхідне для досягнення заданого ступеня перетворення, можна визначити алгебраїчним або графічним способами. Алгебраїчний спосіб застосовують для розрахунку КРІЗ-Б у випадку перебігу в ньому реакцій першого порядку. Цей спосіб базується на складанні матеріального балансу для кожного реактора (ступеня) каскаду.
Розв’язуючи рівняння матеріального балансу для першого реактора каскаду, яке має вигляд
, (3.77)
щодо концентрації реаґенту на виході з реактора, отримаємо
, (3.78)
де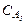 
– концентрація реаґенту А на виході з першого реактора каскаду.
Для другого реактора каскаду
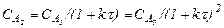, (3.79)
для реактора каскаду з порядковим номером m:
СA,m = CAo/ (1+kt)m. (3.80)
Звідси
. (3.81)
Графічний спосіб розрахунку КРІЗ-Б застосовують для реакцій вищих порядків. Суть методу полягає у графічному розв’язанні системи рівнянь, яка складається з кінетичного рівняння (швидкість реакції виражена згідно із законом діючих мас) та характеристичне рівняння для РІЗ-Б
. (3.82)
Графічний розв’язок отримують, проектуючи точку перетину двох ліній, які описуються зазначеними рівняннями, на вісь абсцис.
Спочатку в координатах СА–uA будують кінетичну криву u = kCAn, задаючись дискретними значеннями СА в межах від САо до нуля. Потім будують лінію, яка відповідає характеристичному рівнянню РІЗ-Б. Для першого реактора каскаду це рівняння матиме вигляд
. (3.83)
Це рівняння описує положення прямої в системі координат СА – uA, для якої
tg a = - 1/t, (3.84)
де a – кут нахилу прямої до осі абсцис, проведеної через точку САо; t – час перебування в реакторі, t = V: UA.
Оскільки переважно масштаби осей концентрації та швидкості реакцій істотно відрізняються (інколи на декілька порядків), то відкладають не кут в його градусному вираженні, а тангенс цього кута. Для такої побудови, очевидно (рис. 3.11), необхідно використати не кут a, а його суміжний кут a1
tg a1 = tg (180о - a) = - tg a = 1/t.
 |
Рис. 3.11. Визначення кількості реакторів у КРІЗ-Б
Для відомих значень V і UA знаходять величину 1/t
. (3.85)
Тангенс кута a, згідно з визначенням цієї тригонометричної функції, відкладають як відношення протилежного катета до прилеглого, тобто DuA/DCA (де DCA = САо – СА1)
. (3.86)
Приймемо, що СА1=0, тоді DCA = САо. Відповідно DuA/DCA = В, а DuA=CAоВ= CAо(UA/V).
Отже, для побудови лінії, що відповідає характеристичному рівнянню РІЗ-Б, на осі абсцис з точки 0 відкладають відрізок, що дорівнює значенню САо і з точки 0 на осі ординат відкладають відрізок, довжина якого визначена за рівнянням (3.86). Через отриману точку і точку з координатами (САо, 0) проводять пряму. Точка перетину двох ліній дає геометричний розв’язок системи рівнянь (3.82). Опустивши з неї перпендикуляр на вісь абсцис, отримують концентрацію реаґенту на виході з першого реактора каскаду. Надалі з точки СА1 проводять пряму, паралельну до першої (за однакових об’ємів усіх реакторів каскаду час перебування в кожному з них, а отже, і кут нахилу буде однаковим). Така побудова виконується до досягнення значення концентрації реаґенту А, яке відповідає заданому ступеню перетворення. Кількість реакторів у каскаді дорівнює кількості елементів побудови.
