Пояснительная записка
к курсовому проекту:
«Математические методы инженерии»
студент: Ожегов М.А.
группы 53304/11
Преподаватель: д.т.н. профессор Востров В.Н.
Санкт-Петербург
2015г
Оглавление
1. Задача №1 нецелочисленное решение графическим методом. 3
2. Задача №1 нецелочисленное решение аналитическим методом. 4
3. Задача №2 целочисленное решение аналитическим методом. 6
4. Задача №2 целочисленное решение графическим методом. 8
Задача №1 нецелочисленное решение графическим методом
Математическая модель задачи.
x 1 - изделие вида P 1;
x 2 - изделие вида P 2;
Прибыль:
L(x)= 4 x1+ 8 x2;
Расход сырья S 1:
Расход сырья S 2:
Маркетинговые исследования показали, что изделий вида P 2 может быть реализовано не больше, чем изделий P 1. Особенности рынка:
Построенные прямые представлены на рисунке 1.
Многоугольник OABC – план решения.
Градиент
Рисунок 1 – Область решения задачи.
Линия уровня касается многоугольника в точке B. Вычислим координаты точки B из пересечения линий (1) и (2).
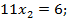
Прибыль в точке B
Прибыль в точке А
Прибыль в точке C
Задача №1 нецелочисленное решение аналитическим методом
x 1 - изделие вида P 1;
x 2 - изделие вида P 2;
Прибыль:
L(x)= 4 x1+ 8 x3;
Запасы сырья S 1:
Запасы сырья S 2:
Маркетинговые исследования показали, что изделий вида P 2 может быть реализовано не больше, чем изделий P 1.
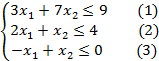
Канонический вид задачи
Технологическая матрица системы 1.
Таблица 1.
| Базисные переменные | Свободные члены | 
| 
| 
| 
| 
|
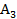
| -9 | |||||
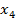
| -4 | |||||
| -1 | |||||
| L | -4 | -8 |
Определяем разрешающую строку
Элемент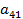 
– разрешающий
Новый базис { 
};
Таблица 2
| Базисные переменные | Свободные члены |
|
|
|
|
|
|
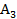
| -3 | 11/2 | -3/2 | |||
| -2 | 1/2 | 1/2 | |||
|
| -2 | 3/2 | 1/2 | |||
| L | -8 | -6 |
Строка X3
+ 
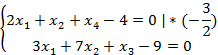
Строка X5
+ 
Строка L
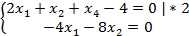
Определяем разрешающую строку
Элемент 
– разрешающий
Новый базис { 
};
Таблица 3
| Базисные переменные | Свободные члены |
|
|
|
|
|
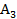
| -6/11 | 2/11 | -3/11 | |||
|
| -38/22 | -1/11 | 28/44 | |||
|
| -13/11 | -3/11 | 20/22 | |||
| L | -124/11 | 12/11 | 4/11 |
Строка X1
+ 
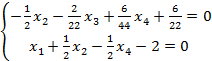
Строка X5
+ 
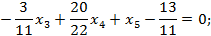
Строка L
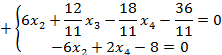
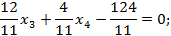
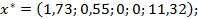
Прибыль предприятия составит:
Для предприятия оптимальным является изготовление 1,73 тонн стального порошка и 0,55 тонн медного порошка, получая прибыль 11,32 тысяч рублей.
Задача №2 целочисленное решение аналитическим методом
Для решения целочисленным методом задачи воспользуемся решением задачи №1 нецелочисленным методом. Где в конечном итоге получили таблицу и оптимальный нецелочисленный план.
Таблица 4
| Базисные переменные | Свободные члены |
|
|
|
|
|
|
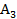
| -6/11 | 2/11 | -3/11 | |||
|
| -19/11 | -1/11 | 7/11 | |||
|
| -13/11 | -3/11 | 10/11 | |||
| L | -124/11 | 12/11 | 4/11 |
Оптимальный план
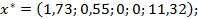
Строим целочисленный план: из таблицы 4 выпишем вторую строку ();
отбросим целую часть, получим неравенство:
Вводим переменную 
;
Каноническая форма
вводим в базис.
Новый базис {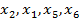 
}
Составляем таблицу 5
| Базисные переменные | Свободные члены |
|
|
|
|
| 
|
|
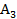
| -6/11 | 2/11 | -3/11 | ||||
|
| -19/11 | -1/11 | 7/11 | ||||
|
| -13/11 | -3/11 | 10/11 | ||||
|
| -8/11 | -1/11 | 7/11 | ||||
| L | -124/11 | 12/11 | 4/11 |
Так как L в столбцах 
> 0, то по теории о двойственности вместо положительных элементов используем отрицательные.
Выбираем столбец .
Определяем разрешающую строку
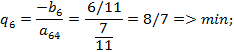
Элемент 
– разрешающий, строку выводим из базиса.
Новый базис { 
};
Строим таблицу 6.
Таблица 6.
| Базисные переменные | Свободные члены |
|
|
|
|
|
|
|
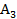
| -6/7 | 1/7 | 3/7 | ||||
|
| -1 | -1 | |||||
|
| -1/7 | -1/7 | -10/7 | ||||
|
| -8/7 | -1/7 | 11/7 | ||||
| L | -76/7 | 8/7 | -4/7 |
Строка X2
+ 
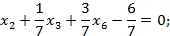
Строка X1
+ 
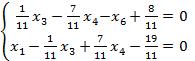
Строка X5
+ 
Строка L
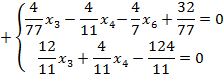
Оптимальный план
Строим целочисленный план: из таблицы 6 выпишем первую строку ();
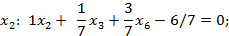
отбросим целую часть, получим неравенство:
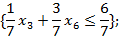
Вводим переменную 
;
Каноническая форма
вводим в базис.
Новый базис { 
}
Таблица 7.
| Базисные переменные | Свободные члены |
|
|
|
|
|
| 
|
|
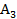
| -6/7 | 1/7 | 3/7 | |||||
|
| -1 | -1 | ||||||
|
| -1/7 | -1/7 | -10/7 | |||||
|
| -8/7 | -1/7 | 11/7 | |||||
|
| 
| 
| 
| 
| ||||
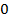
| L | -76/7 | 8/7 | -4/7 |
Выбираем столбец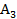
Определяем разрешающую строку
Элемент 
– разрешающий, строку выводим из базиса.
Новый базис { 
};
Строим таблицу 8.
Таблица 8.
| Базисные переменные | Свободные члены |
|
|
|
|
|
|
|
|
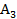
| -1 | |||||||
|
| -1 | -1 | ||||||
|
| -1 | -1 | ||||||
|
| -2 | |||||||
|
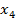
| -6 | |||||||
| L | -4 | -4 | -8 |
Строка X2
Строка X1 остаётся, так как в ней a31=0.
Строка X5
+ 
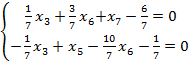
Строка X3
+ 
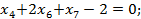
Строка L
Получили целочисленный оптимальный план
