ѕромежуточна€ аттестаци€
—пецификаци€
÷ель работы: определить уровень образовательных достижений учащихс€ по геометрии за ≤ полугодие 7 класса основной школы.
ƒокументы, определ€ющие содержание промежуточной аттестации:
√еометори€ 7-9 классы. ѕрограмма дл€ общеобразовательных организаций.
—оставители: —кафа ≈.»., проректор √ќ”¬ѕќ Ђƒонецкий национальный университетї, заведующа€ кафедрой высшей математики и методики преподавани€ математики √ќ”¬ѕќ
Ђƒонецкий национальный университетї, доктор педагогических наук,
профессор
‘едченко Ћ.я., заведующа€ отделом математики ƒонецкого –»ƒѕќ, доцент, кандидат
педагогических наук
ћаркина ».ј., методист отдела математики ƒонецкого –»ƒѕќ
¬рем€ проведени€: 45 минут
—труктура проверочной работы:
–абота состоит из трех уровней.
”ровень 1 содержит 4 задани€ с выбором ответа. каждому заданию даетс€ 4 варианта ответа, один из которых правильный. ¬ данной части провер€ютс€ усвоение базовых пон€тий, умений и навыков.
—оответствует базовому уровню.
”ровень 2 содержит 2 задани€ (на выбор):
ü задание на установление соответстви€,
ü задание на определение последовательности,
ü задание с кратким ответом,
”ровень 3 содержит 1 задание, требующее полного и обоснованного ответа.
ќценивание работы:
¬ес каждого задани€ при подсчете результата:
уровень 1 Ц 1 балл, уровень 2 Ц 2 балла, уровень 3 Ц 4 балла.
ћаксимальный первичный балл за работу Ц 12 баллов
Ўкала оценивани€:
11-12 баллов Ц Ђ5ї
7-10 баллов Ц Ђ4ї
4-6 баллов Ц Ђ3ї
2-3 баллов Ц Ђ2ї
0-1 баллов Ц Ђ1ї
¬ј–»јЌ“ 1
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. ”кажите точки, принадлежащие пр€мой а.
 ЈC а) ј и ¬ б) C и N;
ЈC а) ј и ¬ б) C и N;
Ј B ЈN в) A,B,N г) N и B
a Ј A
 2. Ќайдите все лучи с началом в точке —
2. Ќайдите все лучи с началом в точке —
 — Ј ¬ а) —ј, —¬; б) —¬, —F,CA;
— Ј ¬ а) —ј, —¬; б) —¬, —F,CA;
ј в) CF,CA г) —F,CB
F
а с 
 Ð(ас)=70∞; Ð(сb)=25∞
Ð(ас)=70∞; Ð(сb)=25∞
3.. Ќайти Ð(аb)
b
а)50∞; б)100∞;
 в)95∞; г)90∞
в)95∞; г)90∞
4. —умма вертикальных углов, полученных при пересечении двух пр€мых, равна 140∞. Ќайти градусные меры всех четырех углов.
а)70∞, 70∞, 110∞, 110∞; б)70∞,70∞, 20∞, 20∞;
в) 140∞, 140∞, 40∞, 40∞; г)20∞, 20∞, 160∞, 160∞
”ровень 2



 «адани€ 5-6 должны содержать краткую запись без обоснований. 5. ¬Ј —Ј јќ=ќ—; ¬ќ=ќD
«адани€ 5-6 должны содержать краткую запись без обоснований. 5. ¬Ј —Ј јќ=ќ—; ¬ќ=ќD

 јЈ D ƒоказать: ¬ќј = —ќƒ
јЈ D ƒоказать: ¬ќј = —ќƒ
6. “очка ћ принадлежит отрезку ≈, длина которого равна 9 см. ќпределите длины отрезков ћ и ≈, если длина отрезка ћ в 3 раза больше длины отрезка ћ≈.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€
7. Ќайдите стороны равнобедренного треугольника, если его периметр равен 28 см, а основание на 8 см меньше боковой стороны.
¬ј–»јЌ“ 2
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
|
|
|
1. ”кажите точки, не принадлежащие пр€мой m



 ј — ¬ а) ј, ¬; б) ¬, , D;
ј — ¬ а) ј, ¬; б) ¬, , D;
m в) ј, ¬, —; г) —, ¬, D;

 K ƒ
K ƒ
 ћ
ћ
 2. Ќайдите все лучи с началом в точке
2. Ќайдите все лучи с началом в точке
Ј — ј) —, ћ; Ѕ) D, ћ;
D ¬) D, —; √) —, ћ, D;


 3. а Ð(ас)=70∞; Ð(св)=20∞
3. а Ð(ас)=70∞; Ð(св)=20∞
 с Ќайти Ð(ав)
с Ќайти Ð(ав)

 ј)90∞; Ѕ)50∞;
ј)90∞; Ѕ)50∞;
в ¬)45∞; √) 100∞
4. —умма вертикальных улов, полученных при пересечении двух пр€мых углов, равна 130∞. Ќайти градусные меры всех четырех углов
ј)130∞, 130∞, 50∞, 50∞; Ѕ)115∞, 115∞, 65∞, 65∞;
¬)90∞, 90∞, 40∞, 40∞; √)30∞, 30∞, 100∞, 100∞;
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
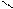





 5. ј ¬ќ=—ќ; Ðјќ¬=Ðјќ—;
5. ј ¬ќ=—ќ; Ðјќ¬=Ðјќ—;

 ƒоказать: јќ¬ = јќ—
ƒоказать: јќ¬ = јќ—


ќ
¬ —
6. “очка — принадлежит отрезку ј¬, длина которого 8 см. ќпределите длины отрезков ј— и ¬—, если длина отрезка ј— в 4 раза меньше длины отрезка ¬—.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€
7. Ќайдите стороны равнобедренного треугольника, если его периметр равен 22см, а бокова€ сторона на 2 см больше основани€.
¬ј–»јЌ“ 3
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. “очка ¬ делит отрезок ј— на два отрезка. Ќайдите длину отрезка ј—, если ј¬ = 7,8 см, ¬— = 2,5см.
а) 15,6 см; б) 5 см;
в) 10,3 см; г) 5,3 см.
2. —умма вертикальных углов, образованных при пересечении двух пр€мых, равна 140º. Ќайдите градусные меры всех четырех углов.
а) 70º, 70º, 110º, 110º; б) 140º, 140º, 40º, 40º;
в) 20º, 20º, 160º, 160º; г) 20º, 20º, 70º, 70º.
3. ƒано: Δ ј¬— = Δ DEF,  ¬ = 73º, ¬— = 6,9 см, DF = 7,6 см. ¬ыберите правильный ответ:
¬ = 73º, ¬— = 6,9 см, DF = 7,6 см. ¬ыберите правильный ответ:
а) DE = 6,9 см, AC = 7,6 cм; б)  , ј— = 7,6 см;
, ј— = 7,6 см;
в) DF = 6,9 см,  ; г) AC = 7,6 см,
; г) AC = 7,6 см,  .
.
4. ≈сли ќN Ц биссектриса  и
и  , то
, то  равен:
равен:
а) 152º; б) 76º;
в) 38º; г) 104º.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. Ћуч ќ— делит угол јќ¬ на два угла. Ќайдите угол —ќ¬, если 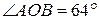 , а угол јќ— на 14º меньше угла —ќ¬.
, а угол јќ— на 14º меньше угла —ќ¬.
6. ¬ треугольнике ј¬— проведена медиана јћ. Ќайдите периметр треугольника ј¬—, если ¬ћ = 4 см, ј¬ = 5 см, а ј— в два раза больше ј¬.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€
7. ¬ треугольнике ј¬— ј¬ = ¬—. Ќа медиане ¬≈ отмечена точка ћ, а на сторонах ј¬ и ¬— Ц точки – и соответственно. (“очки –, ћ и не лежат на одной пр€мой.) »звестно, что  . ƒокажите, что углы ¬–ћ и ¬ ћ равны.
. ƒокажите, что углы ¬–ћ и ¬ ћ равны.
¬ј–»јЌ“ 4
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. “очка ћ делит отрезок – на два отрезка. Ќайдите длину отрезка ћ–, если ћ = 3,7 см, – = 7,2 см.
а) 7,4 см; б) 14,4 см;
в) 10,9 см; г) 3,5 см.
2. —умма вертикальных углов, образованных при пересечении двух пр€мых, равна130º. Ќайдите градусные меры всех четырех углов.
а) 50º, 50º, 130º, 130º; б) 65º, 65º, 115º, 115º;
|
|
|
в) 30º, 30º, 100º, 100º; г) 40º, 40º, 90º, 90º.
3. ƒано: Δ MP— = Δ DAB,  , MP = 12 см, CP = 8 см. ¬ыберите правильный ответ:
, MP = 12 см, CP = 8 см. ¬ыберите правильный ответ:
а) DB = 8 см, AB = 12 cм; б)  , јB = 8 см;
, јB = 8 см;
в) AD = 12 см,  ; г) AB = 12 см,
; г) AB = 12 см,  .
.
4. ≈сли ќN Ц биссектриса  и
и  , то
, то  равен:
равен:
а) 168º; б) 84º;
в) 42º; г) 96º.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. Ћуч ќ≈ делит угол јќ¬ на два угла. Ќайдите угол јќ≈, если  , а угол ¬ќ≈ в три раза меньше угла јќ≈.
, а угол ¬ќ≈ в три раза меньше угла јќ≈.
6. ¬ треугольнике ј¬— проведена медиана ¬≈. Ќайдите длину ј≈, если ј¬ = 6 см, периметр треугольника ј¬— равен 18 см, а ¬— на 2 см больше ј¬.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€
7. Ќа высоте равнобедренного треугольника ј¬—, проведенной к основанию ј—, вз€та точка –, а на сторонах ј¬ и ¬— Ц точки ћ и соответственно. (“очки ћ, и – не лежат на одной пр€мой.) »звестно, что ¬ћ = ¬ . ƒокажите, что углы ¬ћ– и ¬ – равны.
¬ј–»јЌ“ 5
”ровень 1
1. —колько общих точек имеют две пр€мые, которые пересекаютс€?
ј) ќдну общую точку; Ѕ) две общих точки;
¬) не имеют общих точек; √) бесконечное количество точек.
2. акие из приведЄнных записей обозначают угол с вершиной в точке ј?
ј)  NMA; Ѕ)
NMA; Ѕ)  MAE; B)
MAE; B)  CDA; √)
CDA; √)  ACD;
ACD;
3. Ќа какие углы делит развЄрнутый угол его биссектриса?
ј) 40˚и 60 ˚; Ѕ) 90˚ и 90 ˚;  B) 100˚ и 80 ˚; √) 60 ˚ и 60 ˚;
B) 100˚ и 80 ˚; √) 60 ˚ и 60 ˚;
4. ≈сли один из смежных углов равен 142˚, то другой равен:
ј) 100 ˚; Ѕ) 42 ˚; ¬) 38 ˚; √) 36 ˚.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. —умма двух углов, которые образовались при пересечении двух пр€мых, равна 200 ˚. Ќайти каждый из углов, которые образовались при пересечении двух пр€мых.
6. “очка ј отрезка ¬— находитс€ в 3 раза ближе к точке ¬, чем к точке —. Ќайдите ¬ј и —ј, если ¬— = 4,8 см.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€.
7. ¬ равнобедренном треугольнике с периметром 48 см бокова€ сторона относитс€ к основанию как 5:2. Ќайдите стороны треугольника.
¬ј–»јЌ“ 6
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. —колько общих точек имеют две пр€мые, которые не пересекаютс€?
ј) ƒве общих точки; Ѕ) не имеют общих точек; ¬) одну общую точку; √) бесконечное количество точек.
2. ƒл€ угла FKL запишите его вершину и стороны.
ј) K-вершина, KL и KF Цстороны; Ѕ) L -вершина, LF и LK Цстороны;
B) F-вершина, FL и FK Цстороны; √) K-вершина, F K и F L Цстороны;
3. Ќа какие углы делитс€ биссектрисой пр€мой угол?
ј) 30 ˚ и 30 ˚; Ѕ)45 ˚ и 45 ˚; B)60 ˚ и 60 ˚; √)20 ˚ и 70 ˚;
4. ака€ величина каждого из смежных углов, если они между собой равны?
ј) 180 ˚; Ѕ) 90 ˚; ¬) 0 ˚;  √) 60 ˚ и 120 ˚.
√) 60 ˚ и 120 ˚.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. Ќайти каждый из углов, которые образовались при пересечении двух пр€мых, если один из них в 3 раза меньший, чем другой.
6. “очка — отрезка ј¬ находитс€ на 8,6 см ближе к точке ј, чем к точке ¬.
 Ќайдите ј— и —¬, если ј¬ =34 см.
Ќайдите ј— и —¬, если ј¬ =34 см.
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€.
7. ¬ равнобедренном треугольнике с периметром 96 см основание относитс€ к боковой стороне как 2:3. Ќайдите стороны треугольника.
¬ј–»јЌ“ 7
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
|
|
|
1. »спользу€ рисунок,
укажите верное утверждение: 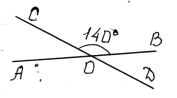
| □ ј | □ Ѕ | □ ¬ | □ √ |
 AOC+ AOC+  BOD=100o BOD=100o
|  AOD= AOD=  BOD как смежные BOD как смежные
|  AOC+ AOC+  BOD=180o как смежные BOD=180o как смежные
|  AO—= AO—=  BOD как вертикальные BOD как вертикальные
|
2. ќпределите, какие три точки K, R и P лежат на одной пр€мой если
| □ ј | □ Ѕ | □ ¬ | □ √ |
| KP=15 дм. PR=21 дм. KR=7дм. | KR=16 дм. RP=9 дм. PK=7дм | PR=3 дм. RK=5 дм. KP=9дм | KP=16 дм. RP=15 дм. KR=2дм |
3. Ћуч OR делит  AOB на два угла. Ќайдите
AOB на два угла. Ќайдите  BOR,если
BOR,если  AOB=78o, ј
AOB=78o, ј  AOR на 18o больше
AOR на 18o больше  BOR
BOR
| □ ј | □ Ѕ | □ ¬ | □ √ |
| 48o | 12o | 30o | 96o |
4. »спользу€ рисунок, укажите верное утверждение дл€ треугольника ABC.

| □ ј | □ Ѕ | □ ¬ | □ √ |
| BF-высота треугольника | BF-биссектриса треугольника | AR- медиана треугольника | AR-высота треугольника |
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. ќдин из смежных углов в 3 раза больше другого. Ќайдите эти углы.
- ¬ треугольнике KRP, KR=RP, KF=FP. “очка F лежит на стороне треугольника KP,
 RKF=64o. Ќайти
RKF=64o. Ќайти  KRF.
KRF.
”ровень 3
- Ќа рисунке отрезки PR=SH, PH=SR.
ƒокажите, что  SRH=
SRH=  PHR
PHR

¬ј–»јЌ“ 8
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. »спользу€ рисунок, укажите верное утверждение.

| □ ј | □ Ѕ | □ ¬ | □ √ |
 COA= COA=  BOD как вертикальные BOD как вертикальные
|  COB= COB=  COD как смежные COD как смежные
|  COA+ COA+  BOD=180o BOD=180o
|  COB+ COB+  BOD=150o BOD=150o
|
2. ќпределите, какие три точки A, B и C лежат на одной пр€мой если:
| □ ј | □ Ѕ | □ ¬ | □ √ |
| AC=7см. AB=3см. ¬—=5см. | AB=7см. AC=5см. CB=2см. | CB=8см. AB=3см. A—=4см. | AC=1см. CB=5см. A¬=10см. |
3. Ћуч OC делит  AOB на два угла. Ќайдите
AOB на два угла. Ќайдите  COB, если
COB, если  AOB=78o, а
AOB=78o, а  AOC на 18o меньше
AOC на 18o меньше  BOC.
BOC.
| □ ј | □ Ѕ | □ ¬ | □ √ |
| 48o | 12o | 30o | 96o |
4. »спользу€ рисунок, укажите верное утверждение дл€ треугольника ABC.

| □ ј | □ Ѕ | □ ¬ | □ √ |
| BK-биссектриса треугольника | BD-биссектриса треугольника | BD-медиана треугольника | BK-медиана треугольника |
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. ќдин из смежных углов в 5 раз меньше другого. Ќайдите эти углы.
6. ¬ треугольнике ABC, AB=AC, BD=DC,  BAD=36o. “очка D лежит на стороне BC. Ќайти
BAD=36o. “очка D лежит на стороне BC. Ќайти  ABD.
ABD.
”ровень 3
7. Ќа рисунке отрезки AB=CD и BD=AC.
ƒокажите, что ∠CAD=∠BDA.

¬ј–»јЌ“ 9
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1.—колько существует разных отрезков, концами которых есть точки ј, ¬, — и ƒ, лежащие на одной пр€мой.
а) 3 б) 6
в) 4 г) 5
2. Ќайдите угол, если биссектриса образует с его стороной угол, который равен 60⁰
а) 30⁰ б) 90⁰
в) 180⁰ г) 120⁰
3. ќдин из смежных углов в 3 раза меньше второго. Ќайдите эти углы.
а) 60⁰ и 120⁰ б) 45⁰ и 135⁰
в) 60⁰ и 20⁰ г) 45⁰ и 15⁰
4. ¬ равнобедренном треугольнике ј¬— с основанием ј— проведена биссектриса ¬ƒ. ќпределите равенство треугольников ј¬ƒ и —¬ƒ.
а) равные; б) определить невозможно;
в) неравные; г) равнобедренные.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
|
|
|
5. Ќайдите углы, полученные при пересечении двух пр€мых, если сумма трех из них равна 285⁰.
6. Ќайдите градусную меру угла ’.

”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€.
7. Ќа сторонах угла ћ отложены равные отрезки ћј и ћ¬. Ќа биссектрисе угла ћ отложены отрезки ћ и ћ—, причем ћ— больше ћ . ƒокажите равенство треугольников — ¬ и — ј.
¬ј–»јЌ“ 10
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1. —колько существует разных отрезков, если три точки ј, ¬, —, лежат на одной пр€мой, а четверта€ ƒ не лежит на пр€мой.
а) 3 б) 5
в) 4 г) 6
2. Ќайдите угол между биссектрисой и стороной угла, который равен 50⁰
а) 130⁰ б) 25⁰
в) 75⁰ г) 100⁰
3. ќдин из смежных углов в 5 раз больше второго. Ќайдите эти углы.
а) 30⁰ и 30⁰ б) 36⁰ и 144⁰
в) 15⁰ и 75⁰ г) 30⁰ и 150⁰
4. ¬ равнобедренном треугольнике ј¬— с основанием ј— проведена медиана ¬ . ќпределите равенство треугольников ј¬ и —¬ .
а) равные; б) определить невозможно;
в) неравные; г) равнобедренные.
”ровень 2
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. Ќайдите углы, полученные при пересечении двух пр€мых, если сумма трех из них равна 300⁰.
6. Ќайдите градусную меру угла ’. 
”ровень 3
–ешение задани€ 7 должно иметь полное обоснование. Ќеобходимо записать последовательные логические действи€ и объ€снени€.
7. Ќа биссектрисе угла отложены отрезки ј и ћ, причем ћ больше ј, а на сторонах угла вз€ты точки ¬ и — так, что ¬ј=ј—, ¬ћ=ћ—. ƒокажите, что треугольники ¬ ј и — ј равны.
¬ј–»јЌ“ 11
”ровень 1
«адани€ имеют по четыре варианта ответов, из которых только один ответ правильный. ¬ыберите правильный, на ваш взгл€д ответ.
1.“очка Ќ Ц середина отрезка –, ј- середина Ќ–. ¬о сколько раз отрезок Ќј меньше отрезка –.
а) в ¼ раз; б) в 3 раза;
в) в 2 раза; г) в 4 раза.
2. Ќайдите смежные углы, если их градусные меры относ€тс€, как 3:7.
а) 18⁰ и 54⁰; б) 18⁰ и 126⁰;
в) 54⁰ и 126⁰; г) 72⁰ и 108⁰;
3. Ѕиссектрисы углов ј и — треугольника ј¬— пересекаютс€ в точке ќ под углом 121⁰. Ќайдите угол ¬.
а) 62⁰; б) 45⁰;
в) 90⁰; г) 59⁰.
4. Ќа рисунке ƒ≈=— ,  —≈ =
—≈ =  ƒ≈—.
ƒ≈—.
 ѕо каким элементам треугольники ƒ≈— и —≈ равные? —
ѕо каким элементам треугольники ƒ≈— и —≈ равные? —
а) по двум сторонам и углу между ними;
б) по стороне и двум прилегающим углам;
в) по трем сторонам; ƒ ≈
г) определить невозможно.
”ровень 2.(каждое задание оцениваетс€ 2 баллами)
«адани€ 5-6 должны содержать краткую запись без обоснований.
5. ќдин из углов, полученных при пересечении двух пр€мых, в 4 раза больше другого. Ќайдите углы.
6. ¬ треугольнике ј¬— проведена медиана јћ. Ќайдите периметр треугольника ј¬—, если ¬ћ =4см, ј¬ =5см, а ј— в 2 раза больше ј¬.
”ровень 3.(каждое задание оцениваетс€ 4 баллами)






