Министерство образования республики Беларусь
Учреждение образования
«Могилевский государственный университет им. А.А. Кулешова»
С.М. Чернов
ОБЩАЯ ФИЗИКА
ФИЗИКА ЯДРА И
ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
Могилев 2014
Тема №1
Размеры атомных ядер
I. Общая теория и рабочие формулы
Вопрос о размерах и форме атомных ядер не является тривиальным. Так как нуклоны подчиняются квантовым законам, то эти " размерные " характеристики следует понимать в квантово-механическом смысле, в частности, плотность распределения электрического заряда и массы внутри ядра следует определять соотношениями:
(1)
Где 
и 
-волновые функции протонов и нуклонов ядра, удовлетворяющие условию нормировки:
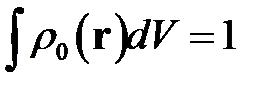. (2)
B дальнейшем будем рассматривать, главным образом, электромагнитные плотности распределения протонов, нормированные условием (2).
Для наглядности часто вводят интегральные характеристики:
Среднеквадратичный электромагнитный радиус ядра Rэл :
(3)
либо эквивалентный радиус ядра 
(радиус равномерно заряженного шара, совпадающего с 
). Различают две группы экспериментов по исследованию структуры ядра: электромагнитные и ядерные. I. Электромагнитные методы: 1. Рассеяние быстрых электронов 
и мюонов (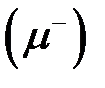
с энергиями Е ≥ 100 МэВ ядрами;
2. Измерение рентгеновских спектров излучения 
-мезоатомов;
3. Анализ кулоновских энергий зеркальных ядер.
Указанные процессы дают информацию о распределении электрического заряда в ядрах, и следовательно определяют электромагнитные радиусы ядер.
II. Ядерные методы:
1. Рассеяние нуклонов и α-частиц, а также некоторых мезонов (π, К) на ядрах с энергиями Е ≥ 10 МэВ;
2. Измерение энергетических спектров α - распадов тяжелых ядер;
3. Исследование зависимости энергии связи ядер от массового числа A и заряда Z.
Эти эксперименты с сильновзаимодействующими частицами фактически несут информацию о размерах области действия ядерных сил, определяющие распределение массы внутри ядра, т.е. p и n.
Результаты, полученные разными методами, оказались близкими. Таким образом, можно считать, что в атомных ядрах распределение массы и электрического заряда практически совпадают. Учитывая данное обстоятельство, при исследовании структуры ядра будем рассматривать лишь более простые и более точные электромагнитные методы (ядерные методы будут рассмотрены в других темах).
1. Упругое рассеяние быстрых электронов на ядрах.
В опытах по электронному рассеянию экспериментально измеряют дифференциальное сечение рассеяние σ, которое определяется как отношение числа частиц, рассеянных в секунду и телесной угол dΩ к первоначальному потоку падающих частиц. Расчеты показывают, что сечение рассеяния имеет вид:
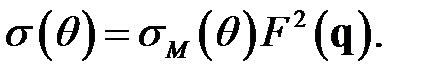(4)
Здесь 
- электрический форм-фактор, связанный с 
обратным Фурье-преобразованием:
(5)
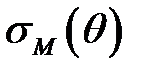- сечение рассеяния Мотта, определяющее рассеяние релятивистского электрона на точечном ядре, которое в ультрарелятивистском приближении (Е 
meс2) имеет вид: 
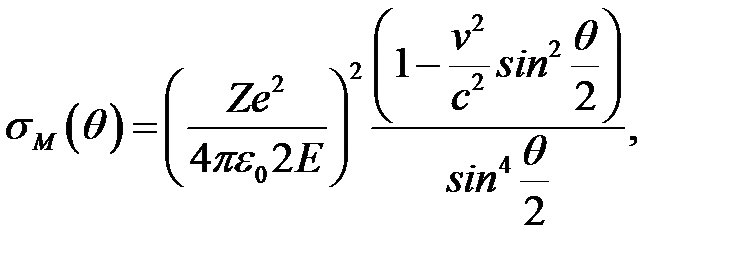(6)
где E - энергия электронов в с.ц.м.; ϴ - угол рассеяния; ħ q -вектор передачи импульса электроном ядру: q = 
. (7)
Экспериментально измеренное сечение рассеяние (или форм - фактор F(q)) позволяют определить плотность распределения протонов в ядре с помощью прямого Фурье - преобразования:
(8)
2. Рентгеновские спектры излучения µ - мезоатомов.
В природе существует элементарная частица - мюон (µ-) (старое, ошибочное название µ - мезон), которая также как и электрон не участвует в сильных взаимодействиях, имеет массу m µ = 105,7 МэВ = 206,7 m e с временем жизни τ = 2,2 
-6с. Мюон, попавший в вещество, за счет электромагнитных сил может быть захвачен ядром и образует связанную систему, подобную обычным атомам. Такая система называется мезоатомом. Как правило, захват мюона происходит на возбужденные уровни с временем жизни порядка 10-8 с. При переходе мезоатома в основное состояние испускается квант энергии порядка МэВ (область жесткого рентгеновского диапазона). Как и любое излучение, оно несет информацию о структуре энергетических уровней атома. Однако в отличие от обычных (электронных) атомов, энергетический спектр мезоатома в большей степени зависит от размеров ядра. Измерение энергии квантового перехода позволяет определять RЭл.
3. Анализ кулоновских энергий зеркальных ядер.
Изобарные ядра (А =const) называются зеркальными, которые отличаются заменой протонов на нейтроны. Примерами пар зеркальных ядер являются: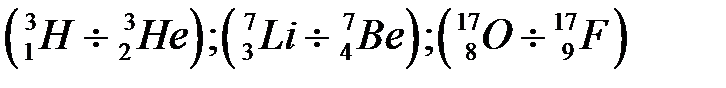 
. Опыт показывает, что энергии связи зеркальных ядер различны, причем эта разность 
(А) растет с ростом массового числа А. Например: 
Если предположить, что нуклоны в ядре ведут себя одинаковым образом по отношению к ядерному взаимодействию, то указанная разность энергий связи определяется дополнительным кулоновским отталкиванием "лишнего" протона в поле остальных протонов и, следовательно, имеет чисто электромагнитное происхождение. В простейшем предположении однородного распределения электрического заряда внутри шара радиуса Ro кулоновская энергия взаимодействия протона с полем шара заряда Ze равна:
(9)
Измеряя экспериментально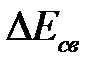 
, можно определить Ro.
Приведенные методы измерения размеров ядра приводят к близким значениям Ro, которые связаны с массовым числом A приближенным условием:
, (10)
где эмпирическая постоянная r o = (1,2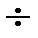 
1,5) Фм (1Ферми = 1Фм = 10-15 м).
Тема № 2
Энергия связи и масса атомных ядер
I. Общая теория и рабочие формулы
Как известно, все стабильные и долгоживущие атомные ядра (τ≥10-10 с)состоят из протонов и нейтронов(нуклонов). Для дальнейших численных расчетов укажем массы нуклонов и электронов:
Таблица 1. Массы нуклонов и электронов.
| Частица | Масса (mo) | |||
| кг | в единицах me | а.е.м. | moc2 (МэВ) | |
| Протон (p) | 1,6726  10-27
| 1836,15 | 1,007276 | 938,279 |
| Нейтрон (n) | 1,6749  10-27 
| 1838,68 | 1,008665 | 939,573 |
| Электрон (e) | 9,1105  10-31
| 1 | 5,48  10-4
| 0,511 |
В таблице указана одна внесистемная единица измерения массы микрочастиц - атомная единица массы (а.е.м.). За 1 а.е.м. принимается 
часть массы нейтрального атома изотопа углерода 
: 1 а.е.м. = 1,6605 
10-27 кг = 931,502 МэВ. Важнейшим параметром ядра 
, характеризующим его прочность, является энергия связи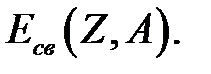 
Энергией связи ядра (относительно всех нуклонов) называется минимальная энергия, которую необходимо сообщить ядру, чтобы расщепить его на составляющие нуклоны. Для стабильных ядер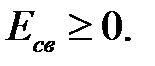 
Заметим, что внутренняя энергия ядра отличается от энергии связи знаком 
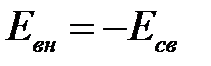. Знание энергий связи ядер позволяет рассчитать энергетический баланс не только для процесса полного расщепления, но и для любых процессов распадов и взаимных превращений ядер. Например, для выбивания из ядра α - частицы необходимо затратить энергию 
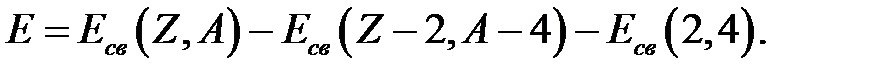
В силу известного соотношения между энергией и массой (
) 
можно записать в виде:
(1)
где масса выражена в кг. Из соотношения (1) следует, что масса стабильного ядра (Есв≥0) меньше суммы отдельных нуклонов на величину 
, которая определяется путем введения понятия дефекта массы ядра.
Дефектом массы ядра в ядерной физике называется разность между массой ядра, выраженной в а.е.м. и соответствующим массовым числом:
(2)
В частности, из таблицы 1 дефекты масс p и n (а также α - частицы) равны:
Связь энергии связи с дефектами масс можно записать по аналогии с (1) в виде:
(3)
Например, для α - частицы имеем: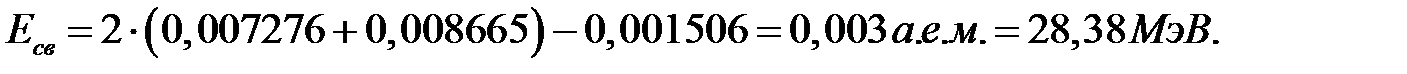 
Важнейшей задачей ядерной физики является получение зависимости 
из всей совокупности ядерно - физических данных. Наиболее прозрачная зависимость получается в жидко-капельной модели ядра:
(4)
Где a 1 = 15,75 МэВ; a 2 = 17,80 МэВ; a 3 = 0,71 МэВ; a 4 = 23,70 МэВ; a 5 = 12,0 МэВ;
Зависимость (4) называется полуэмпирической формулой Бете - Вайцзеккера (Б.В.).
III. Примеры решения задач
Задача 1. Используя формулу Б.В. (4), оценить коэффициент поверхностного натяжения σ ядерной матери.
Решение:
Для оценки σ воспользуемся формулой, связывающей радиус ядра R c массовым числом А:
(1.1)
Считая ядро шаром радиуса R, поверхностную энергию ядра можно записать в виде:
(1.2)
С другой стороны, из формулы Б.В.(4) 
, где 
2 = 17,8 МэВ = 2,85 
Дж. Отсюда для σ имеем:
. (1.3)
Численно σ равно: σ = 
Для сравнения, вода имеет σ = 7,3 
. Объяснить качественно разницу полученных результатов.
Ответ: σ = 1,57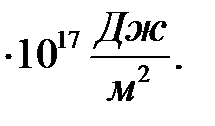 
Задача2. Считая деформированное ядро симметричным относительно вращения вокруг оси Z, а координаты точек на его поверхности в полярных координатах описываются функцией 
. Представив разложение функции R(ϑ) в ряд по полиномам Лежандра Рn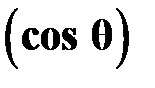 
в виде:
, (2.1)
где Ro - радиус недеформированного ядра - шара,
(2.2)
