Теоретические положения
Под действием внешних сил твердые тела могут деформироваться, то есть изменять свои размеры и форму. Если после прекращения действия внешних сил, вызвавших деформацию, тело принимает первоначальные размеры и форму, то деформацию называют упругой.
На пружину, изображенную на рисунке 7.1, действует направленная вертикально вниз сила 
. Под действием этой силы пружина деформируется, и ее длина возрастает. Упругая сила 
, возникающая в пружине вследствие ее деформации, уравновешивает внешнюю силу . Силы и равны по модулю и направлены в противоположные стороны.
В соответствии с законом Гука при упругой деформации пружины
,
где k, 
– жесткость пружины и изменение ее длины соответственно.
Жесткость пружины характеризует ее упругие свойства.
Рассмотрим две пружины, соединенные последовательно, как это изображено на рисунке 7.2. Если к нижней пружине приложить направленную вертикально вниз внешнюю силу , то в соответствии с третьим законом Ньютона равная ей по модулю направленная вертикально вниз сила будет действовать и на вторую пружину со стороны первой.
Под действием силы пружины деформируются. Пусть изменение длины первой пружины равно 
, а второй пружины – 
. Тогда в соответствии с законом Гука
 ,
| (7.1) |
 ,
| (7.2) |
где 
– жесткость первой и второй пружин соответственно.
Жесткость системы двух последовательно соединенных пружин
 ,
| (7.3) |
Подставляя в это выражение значения и из формул (7.1) и (7.2), получаем
 ,
| (7.4) |
В общем случае при последовательном соединении n пружин
,
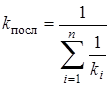где 
– жесткость 
-й пружины.
На рисунке 7.3 изображены две параллельно соединенные пружины, нижние концы которых закреплены на горизонтальной перемычке. Если на перемычку подействовать направленной вертикально вниз силой , то произойдет деформация пружин. Со стороны перемычки на первую пружину будет действовать сила 
, а на вторую пружину – сила 
. В соответствии с законом Гука
 ,
| (7.5) |
 ,
| (7.6) |
где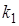 
, 
– жесткость первой и второй пружин соответственно; – изменение длины каждой из пружин.
Жесткость системы двух параллельно соединенных пружин
.
Так как 
, то, подставляя значения и из формул (7.5) и (7.6), получаем
 ,
| (7.) |
В общем случае при параллельном соединении n пружин
,
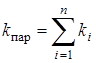где – жесткость -й пружины.
Экспериментальная установка
В лабораторной работе экспериментально определяется жесткость пружины и системы пружин. Схема экспериментальной установки изображена на рисунке 7.4.
Один конец пружины закреплен на основании стойки, а второй ее конец соединен с нитью. Нить перекинута через шкив, установленный в верхней части стойки, а свободный конец нити соединен с подвесом массой 
. На пружину со стороны нити действует сила
.
Расстояние от основания стойки до нижнего торца подвеса равно l 0 . Установка на подвес дополнительного груза массой m приводит к изменению длины пружины на величину
 ,
| (7.8) |
где l – расстояние от основания стойки до нижнего торца подвеса после установки на него груза массой m.
Увеличение массы подвешенного груза приводит к появлению дополнительной силы, действующей на пружину:
.
С другой стороны в соответствии с законом Гука
.
Приравниваем правые части двух последних формул и выражаем жесткость пружины
 .
| (7.9) |
