Наряду с конденсацией водяного пара в атмосфере наблюдается замерзание водяных капель. Известно, что поверхностная энергия на границе пар–вода меньше, чем на границе пар–лед. Поэтому первичным процессом в естественных условиях при всех температурах является конденсация водяного пара, сопровождающаяся образованием капель воды. Водяные капли при отрицательных температурах могут замерзнуть и образовать ледяные частицы. По современным представлениям, для образования ледяной фазы необходимо, чтобы внутри водяной капли сформировался зародыш новой фазы – льда. Такой фазовый переход называется гомогенным. Зародыш новой фазы может образоваться и на некотором инородном ядре, который по аналогии с ядром конденсации носит название ядра кристаллизации. В данном случае имеет место гетерогенный фазовый переход.
Рассмотрим условия гомогенного фазового перехода. В результате случайных (флуктуационных) движений молекул жидкости внутри нее могут образоваться скопления, имеющие плотность и структуру льда. Вероятность образования таких скоплений увеличивается с понижением температуры. Образовавшиеся зародыши ледяной фазы становятся устойчивыми лишь при некоторых условиях, а именно при достижении определенного размера. На формирование зародыша необходимо затратить энергию, которая пропорциональна его поверхности. В то же время при возникновении ледяной фазы выделяется энергия скрытой теплоты замерзания. Пока зародыш очень мал, скрытая теплота, пропорциональная его объему, меньше, чем энергия образования поверхности, и возникший зародыш снова распадается. Чтобы это не произошло, необходимо совершить внешнюю работу. Работа образования зародыша вначале растет с увеличением его размера. По достижении некоторого критического размера rкр работа достигает максимума. Если размер больше критического, то в дальнейшем увеличение размера ведет к уменьшению необходимой работы.
Найдем критический размер и максимальную работу образования зародыша, исходя из термодинамических представлений. Будем считать, что ледяной зародыш имеет форму сферы радиусом r. Пусть Фв и Фл – удельные термодинамические потенциалы воды и льда соответственно. Работа образования зародыша А будет определяться изменением термодинамического потенциала (Фл – Фв) 4/3 πr 3 ρл и поверхностной энергией зародыша 4 πr 2 σл (σл – коэффициент поверхностного натяжения на границе лед–вода, ρл – плотность льда).
Общая работа образования зародыша выразится формулой
А = (Фл – Фв) 4/3 πr 3 ρл + 4 πr 2 σл. (2.6)
Ледяная фаза при отрицательных температурах является более устойчивым состоянием, чем переохлажденная вода. Известно, что при переходе некоторой системы в более устойчивое состояние термодинамический потенциал уменьшается, поэтому Фв > Фл.
Чтобы определить критический радиус зародыша rкр, используем известное условие достижения максимума (dA / dr) = 0 (при r = rкр), которое принимает вид
8 πrкр σл – (Фв – Фл) 4 πrкр 2 ρл = 0. (2.7)
Отсюда
(Фв – Фл) = 2 σл / ρл rкр. (2.8)
Таким образом, критический радиус зародыша определяется разностью термодинамических потенциалов, зависящих от температуры и давления. Для установления связи rкр с последними величинами перепишем (2.8) в дифференциальном виде:
dФв – dФл = 2 σл / ρл d (1 / rкр), (2. 9)
при этом мы пренебрегли зависимостью σл и ρл от температуры и давления.
Поскольку для состояния насыщения дифференциал термодинамического потенциала равен
dФ = v dЕ – φ dT,
то в соответствии с этим вошедшие в (1.16) дифференциалы равны
dФ в = – φ в dT + v в dp, (2.10)
dФл = – φ л + v л dp, (2.11)
где φ в и φ л – энтропии воды и льда соответственно; vв и vл – их удельные объемы.
Для большинства жидкостей и твердых тел при наблюдаемых в атмосфере dT и dp вторые слагаемые в правых частях последних соотношений на несколько порядков меньше первых. Пренебрегая по этой причине членами с dp, запишем уравнение (2.9) с учетом (2.10) и (2.11) в виде
– (φв – φл) dT = 2 σл / ρл d (1 / rкр) (2.12)
Если еще воспользоваться формулой энтропии для обратимых процессов
или dq = T dφ,
то последнее уравнение примет вид
2 σл / ρл d (1 / rкр) = – Lпл dT / T, (2.13)
где Lпл – удельная теплота плавления льда.
Если проинтегрировать левую часть (2.13) от 0 до rкр, а правую часть от Т0 до Т, то получим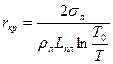 
, (2.14)
где Т0 = 273.16 К – температура тройной точки.
Максимальная работа образования зародыша определяется выражением
Aмакс = 4/3 π r2 σл (
) (2.15)
или
Aмакс = 1/3 σл S, (2.16)
где S – поверхность зародыша.
Последняя формула пригодна и в том случае, если зародыш не имеет сферической формы.
Из формулы (2.14) следует, что критический радиус зародыша существенно зависит от переохлаждения (Т0 – Т). Чем больше переохлаждение, тем меньше критический радиус, тем легче образоваться устойчивому зародышу. В свободной атмосфере активных ядер кристаллизации мало, поэтому замерзание капель начинается при достаточно большом переохлаждении.
