Последовательность решения задачи

1. Указывают точку, равновесие которой рассматривается. В задачах для самостоятельной работы такой точкой является центр тяжести тела или точка пересечения всех стержней и ни­тей.

2. Прикладывают к рассматриваемой точке активные силы. В задачах для самостоятельной работы активными силами явля­ются собственный вес тела или вес груза, которые направлены вниз (правильнее — к центру тяжести земли). При наличии блока вес груза действует на рассматриваемую точку вдоль нити. Направление действия этой силы устанавливается из чертежа. Вес тела принято обозначать буквой G.

3. Мысленно отбрасывают связи, заменяя их действие реакция­ми связей. В предлагаемых задачах используются три вида свя­зей — идеально гладкая плоскость, идеально жесткие прямоли­нейные стержни и идеально гибкие нити, — в дальнейшем име­нуемые соответственно плоскостью, стержнем и нитью.

При замене связей их реакциями следует помнить, что реак­ция плоскости направлена по нормали (перпендикуляру) к ней в точке контакта (соприкосновения), а реакции стержня и нити — по их осям. При этом реакция плоскости направлена от нее и проходит через центр тяжести тела, а реакция нити — от рас­сматриваемой точки или тела (нить всегда испытывает растяже­ние). Направление реакции стержня заранее неизвестно, поэто­му оно может быть принято произвольно. Если направление ре­акции стержня трудно определить из схемы, то его принимают растянутым, и реакцию направляют от рассматриваемой точки. Истинное направление будет установлено после решения урав­нений.

Реакции нити и стержня принято называть усилиями. Реак­цию плоскости обозначают буквой R, а усилие в нити и стерж­не — S или N. В дальнейшем, если не указывается вид связи или говорится о разных связях, то будет применяться термин «реак­ция».

К рассматриваемой точке прикладывают реакции связей. Луч­ше сделать это на отдельном чертеже, выполненном схематиче­ски, придерживаясь масштаба при изображении углов. В резуль­тате получают систему трех сходящихся сил. Активная сила (груз или собственный вес тела) известна, а реакции связей (их две) не­известны.

4. Выбирают положение прямоугольной системы координат. Начало координат совмещают с точкой, равновесие которой рас­сматривается. Положение осей может быть выбрано произволь­но и на конечном результате при правильном решении это не отражается. Обычно используют один из двух приемов для выбо­ра направления осей координат. Первый: одну из осей (любую) направляют так, чтобы она совпала с направлением одной из не­ известных реакций, а другая при этом составляла бы с первой угол 90°. Второй: ось у направляют вертикально, а ось х — гори­зонтально. В частном случае возможен еще один прием для рас­положения осей: если система сил имеет ось симметрии, то одну из координатных осей совмещают с ней.

Во всех случаях следует определить углы между реакциями и координатными осями и указать их на чертеже.

5. Составляют уравнения равновесия вида:

Напомним, что проекцией силы на ось является произведение модуля (величины) этой силы на косинус угла между направления­ми действия силы и оси. Если угол между направлениями силы и оси острый, то перед величиной проекции ставится знак «плюс», т. е. сила и ось направлены в одну сторону, если они направлены в противоположные стороны, то ставиться знак «минус».

Решают систему двух уравнений с двумя неизвестными. При этом если одна из осей совпадает с неизвестной реакцией, то одно из двух уравнений содержит только одно неизвестное, что упрощает решение системы.

Если ответ получится со знаком «минус», то это означает, что направление реакции на чертеже было выбрано неверно, т.е. если до составления уравнений равновесия стержень предпола­гался растянутым, то в действительности он будет сжатым, и на­оборот. Такой ответ не является ошибкой решения (если оно выполнено верно), так как чертеж и ответ вместе дают возмож­ность указать истинное направление реакции.

6. Выполняют проверку решения. Обычно она делается графи­ческим или другими способами, но может быть выполнена и аналитически. Для этого следует изменить положение осей ко­ординат и решить задачу в новой системе. Ответы должны быть одинаковыми.

Пример 1. Определить величину и направление реакций свя­зей для схемы, приведенной на рис. 1, а под действием груза G = 30 кН. Проверить правильность определения реакций.

Решение.

1. В задаче рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на нити. Заменим тело тонкой 0, совпадающей с центром тяжести.

2. Приложим к точке 0 активную силу, которой является соб­ственный вес тела G. Направим ее вниз (рис. 1, б).

3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обо­значим ее R) проходит по нормали к плоскости в точке А, а реакция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересе­каться в точке 0.

Изобразим действующие силы в виде системы трех сходя­щихся сил на отдельном чертеже (рис. 1, в).

Рис. 1

4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. 1, г). Определим углы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, а сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было бы другим.

5. Составим сумму проекций всех сил на оси координат:

1) ;

2) .

Решим систему уравнений. Из второго уравнения находим

кН.

Из первого уравнения находим

кН.

6. Проверим решение, для чего расположим оси координат, как показано на рис. 1, д. Составим уравнения равновесия для вновь принятых осей:

1) ;

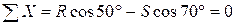2) .

Решим систему уравнений способом подстановки. Из первого уравнения найдем R:

.

Подставим это выражение во второе уравнение:

,

откуда

кН.

Теперь найдем R:

кН.

Очевидно, что при расположении осей, как показано на рис. 1, д, вычисления оказались более сложными.

Ответ: R = 11,84 кН; S = 22,27 кН.

Пример 2. Определить усилия в нити и стержне кронштейна, показанного на рис. 2, а, если G = 20 кН.

Решение.

1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.

2. Активной силой является вес груза G, направленный вниз (рис. 2, б).

3. Отбросим связи: стержень и нить. Усилие в нити обозна­чим S ₁и направим от точки А,так как нить может испытывать только растяжение. Усилие в стержне обозначим S ₂и тоже на­ правим от точки А,предполагая что стержень АС растянут (рис. 2, б).

 

Рис. 2

Выполним на отдельном чертеже схему действия сил в точке А (рис. 2, в).

4. Выберем положение системы координат. Начало коорди­нат совмещаем с точкой А (рис. 2, г). Ось х совмещаем с лини­ей действия усилия S ₁а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями S ₁и S ₂.

5. Составим уравнения равновесия:

1) ;

2) .

Из второго уравнения находим

кН.

Из первого уравнения находим

кН.

Знак «минус» перед S₂ свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.

6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. 2, д.

Ответ: S ₁= 15,56 кН, S ₂ = –29,24 кН (при принятом на черте­же направлении усилий).

Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. 2, а угол 70° заменить на 60°, сохранив угол 30°, то усилия будут равны: S ₁= 20 кН, S ₂ = –34,64 кН. А при угле 50° S ₁ = 29,26 кН, S₂ = –44,8 кН. Оба усилия растут и становятся больше веса груза.

Пример 3. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. 3, а?

Остальные данные — в примере 2.

Рис. 3

Решение.

1. Рассматриваемой точкой остается точка А.

2. Активная сила (вес груза G) действует на точку горизон­тально слева направо, так как груз перекинут через блок.

3. Усилия S ₁ и S ₂ прикладываем к точке А, как в примере 2.

4. Выбираем систему координат, как показано на рис. 3, б.

5. Составляем и решаем уравнения равновесия:

l) ;

2) .

Из первого уравнения находим

кН.

Из второго уравнения находим

кН.

Ответ: S ₁ = 26,94 кН; S ₂ = –10,64 кН при принятом направле­нии усилий на чертеже. Усилие S ₁увеличилось, S ₂ — уменьши­лось, а знаки не изменились.

Задание для практического решения №1. Определить величину и на­правление реакций связей по данным одного из вариантов, показан­ных на рис. 4. Проверить правильность определения реакций аналитическим способом.

Рис. 4

Рис. 4. Продолжение

Рис. 4. Продолжение

Рис. 4. Продолжение

Рис. 4. Окончание

 

Контрольные вопросы.

1. Какие силы называются сходящимися?

2. Какая система сходящихся сил называется плоской и пространственной?

3. Как геометрически определяется равнодействующая системы сходящихся сил, влияет ли порядок сложения сил на величину и направление равнодействующей?

4. В чём состоит геометрическое условие равновесия системы сходящихся сил?

5. Что называется проекцией силы на ось, как определяется знак проекции?

6. Сколько и какие уравнения можно составить для уравновешенной плоской системы сходящихся сил?

7. Как формулируют аналитическое условие равновесия системы сходящихся сил?

Задача №2

Построение эпюр продольных сил, нормальных напряжений, определение абсолютного удлинения (укорочения) стержня при растяжении и сжатии

Цель работы – научиться определять главные центральные моменты инерции фигуры, составленной из стандартных профилей проката.

Информационное обеспечение: