—лучайна€ величина ’ называетс€ непрерывной, если ее функци€ распределени€ непрерывна и имеет производную.
ак уже было показано в разделе 4 (формула 4.2), функцией распределени€ случайной величины ’ называетс€ функци€ F(X), выражающа€ веро€тность выполнени€ услови€ 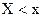 :
:
 (5.1)
(5.1)
‘ункци€ распределени€ обладает следующими свойствами:
1.¬еро€тность попадани€ случайной величины в промежуток от 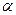 до
до  равна приращению функции распределени€ на концах этого промежутка:
равна приращению функции распределени€ на концах этого промежутка:
 (5.2),
(5.2),
так как веро€тность любого отдельного значени€ случайной величины равна нулю, если функци€ распределени€ непрерывна при этом значении, т. е.:
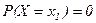 , когда F(X) - непрерывна в точке
, когда F(X) - непрерывна в точке  =
= 
2.‘ункци€ распределени€ удовлетвор€ет услови€м:
 (5.3)
(5.3)
ѕлотностью распределени€ (дифференциальной функцией) непрерывной случайной величины называетс€ функци€
f(x) =  (x). (5.4)
(x). (5.4)
ѕлотность распределени€ любой случайной величины неотрицательна: 
Ќесобственный интеграл от дифференциальной функции в пределах от -  до +
до +  равен 1:
равен 1:
 (5.5)
(5.5)
√рафик функции y = f(x) называетс€ кривой распределени€ или графиком плотности распределени€. рива€ y = f (x) располагаетс€ над осью абсцисс.
¬еро€тность попадани€ случайной величины в промежуток от  до
до  может быть вычислена по формуле:
может быть вычислена по формуле:
 (5.6)
(5.6)
ѕодинтегральное выражение f(x)dx называетс€ элементом веро€тности. ќно выражает веро€тность попадани€ случайной точки в промежуток между точками х и  , где
, где 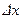 бесконечно мала€ величина.
бесконечно мала€ величина.
‘ункци€ распределени€ F(x) выражаетс€ через плотность f(x) формулой:
 (5.7)
(5.7)
ћатематическое ожидание непрерывной случайной величины ’ вычисл€етс€ по формуле:
 (5.8),
(5.8),
дисперси€  (5.9)
(5.9)
Ќормальное распределение
≈сли плотность распределени€ (дифференциальна€ функци€) случайной переменной определ€етс€ выражением:
 (5.10)
(5.10)
то говор€т, что ’ имеет нормальное распределение с параметрами а и  . ¬еро€тностный смысл параметров:
. ¬еро€тностный смысл параметров: 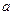 =ћ(X), а
=ћ(X), а 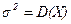 . ќбозначение:
. ќбозначение:
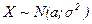
ƒл€ расчета веро€тности попадани€ нормально распределенной случайной величины ’ в промежуток от  до
до  используетс€ формула:
используетс€ формула:
 (5.11)
(5.11)
 (интеграл Ћапласа)
(интеграл Ћапласа)
‘ормула (5.11) иногда в литературе называетс€ интегральной теоремой Ћапласа.
‘ункци€  обладает свойствами:
обладает свойствами:

3 )  (см. таблицу приложени€ 2).
(см. таблицу приложени€ 2).
‘ункци€  табулирована. ¬ частности дл€ симметричного относительно а промежутка
табулирована. ¬ частности дл€ симметричного относительно а промежутка  имеем:
имеем:
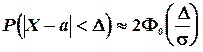 (5.12)
(5.12)
‘ормула (5.12) применима и к частоте m, поскольку ее закон распределени€ при достаточно большом числе испытаний практически совпадает с нормальным. ѕрименительно к случайной величине m, с учетом ее числовых характеристик
M(m) = np и  (5.13)
(5.13)
формула (5.12) примет вид:
 (5.14)
(5.14)
‘ормула (5.12) может быть применена и к относительной частоте  с числовыми характеристиками
с числовыми характеристиками 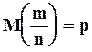 и
и 
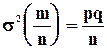
 (5.15)
(5.15)
 (5.16)
(5.16)
— веро€тностью, очень близкой к единице (равной  нормально распределенна€ случайна€ величина ’ удовлетвор€ет неравенству:
нормально распределенна€ случайна€ величина ’ удовлетвор€ет неравенству:
 (5.17)
(5.17)
¬ этом состоит правило трех сигм: если случайна€ величина распределена по нормальному закону, то ее отклонение от математического ожидани€ практически не превышает  .
.
|
|
|
Ћокальна€ теорема ћуавра-Ћапласа. ѕри р 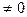 и p
и p  1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидани€ и дисперсии совпадают), т.е. имеет место равенство:
1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидани€ и дисперсии совпадают), т.е. имеет место равенство:
 , где
, где  , a =nр
, a =nр
“огда:
 (5.18)
(5.18)
дл€ достаточно больших n (здесь  (х) - плотность веро€тностей стандартной нормальной случайной величины
(х) - плотность веро€тностей стандартной нормальной случайной величины  и
и  ).
).
ѕример 5.1. Ќа рынок поступила крупна€ парти€ гов€дины. ѕредполагаетс€, что вес туш - случайна€ величина, подчин€юща€с€ нормальному закону распределени€ с математическим ожиданием а = 950 кг и средним квадратическим отклонением s = 150 кг. ќпределите веро€тность того, что вес случайно отобранной туши:
а) окажетс€ больше 1250 кг;
б) окажетс€ меньше 850 кг;
в) будет находитьс€ между 800 и 1300 кг;
г) отклонитс€ от математического ожидани€ меньше, чем на 50 кг;
д) отклонитс€ от математического ожидани€ больше, чем на 50 кг;
е) Ќайдите границы, в которых отклонение веса случайно отобранной туши от своего математического ожидани€ не превысит утроенного среднего квадратического отклонени€ (проиллюстрируйте правило трех сигм);
ж) — веро€тностью 0,899 определите границы, в которых будет находитьс€ вес случайно отобранной туши. акова при этом условии максимальна€ величина отклонени€ веса случайно отобранной туши от своего математического ожидани€?
–ешение. а) ¬еро€тность того, что вес случайно отобранной туши окажетс€ больше 1250 кг Ц можно понимать как веро€тность того, что вес случайно отобранной туши окажетс€ в интервале от 1250 кг до +∞.
‘ормула расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной велечины ’ имеет вид:
 ,
,
где ‘0(z) - функци€ Ћапласа:

‘ункци€ ‘0(z) €вл€етс€ нечетной функцией; т.е. ‘0(-z) = -‘0(z).
Ќайдем веро€тность того, что вес случайно отобранной туши окажетс€ больше 1250 кг. ѕо условию: a = 1250, b = +¥, а = 950, s = 150.
»спользуем формулу расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной величины ’.

Ќайдем по таблице функции Ћапласа (ѕриложение 2) значени€ ‘0(z).
«начени€ ‘0(+¥) в таблице нет. ќднако известно, что ‘0(z) Ѓ 0,5 при
z Ѓ + ¥.”же при z = 5 ‘0(z = 5) = 0,49999997ї 0,5. ќчевидно, что ‘0(+¥) - величина бесконечно близка€ к 0,5. ‘0(-¥) - величина бесконечно близка€ к -0,5.
ѕо таблице функции Ћапласа ‘0(2) = 0,47725.
ќтсюда: P(X>1250) = 0,5 - 0,47725 = 0,02275.
»так, веро€тность того, что вес случайно отобранной туши окажетс€ больше 1250 кг, составл€ет 0,02275.
ѕроиллюстрируем решение задачи графически (рис.5.1).
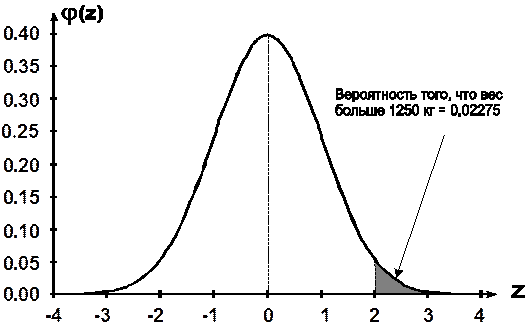
–ис.5.1 √рафическа€ интерпретаци€ к примеру 5.1.
»так, нам задана нормально распределенна€ случайна€ величина ’ с математическим ожиданием а = 950 кг. и средним квадратическим отклонением s = 150 кг., то есть ’ ~N(950;1502). ћы хотим найти веро€тность того, что ’ больше 1250, то есть определить –(’ > 1250). ѕреобразуем ’ в Z, и тогда искома€ веро€тность определитс€ по таблице ѕриложени€ 2 стандартного нормального распределени€.  .
.

“очка z = 0 соответствует математическому ожиданию, то есть а = 950 кг.
б) ¬еро€тность того, что вес случайно отобранной туши окажетс€ меньше 850 кг - это, то же самое, что веро€тность того, что вес случайно отобранной туши окажетс€ в интервале от -¥ до 850 кг.
|
|
|
ѕо условию: a = -¥, b = 850, а = 950, s = 150.
ƒл€ расчета искомой веро€тности используем формулу расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной величины ’.
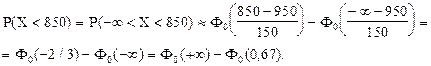
—огласно свойству функции Ћапласа:
-‘0(-¥) = ‘0(+¥),
а ‘0(-0,67) = -‘0(0,67).
Ќайдем по таблице функции Ћапласа (ѕриложение 2) значени€ ‘0(z).
‘0(+¥)ї 0,5;
‘0(0,67) = 0,24857.
ќтсюда: P(X < 850) = 0,5 - 0,24857 = 0,25143.
¬еро€тность того, что вес случайно отобранной туши окажетс€ меньше 850 кг составл€ет 0,25143.
ѕроиллюстрируем решение задачи графически (рис. 5.2).

–ис.5.2. √рафическа€ интерпретаци€ к примеру 5.1.
ѕо условию данной задачи точка на оси абсцисс (z = -0,67) соответствует х = 850, т.е. весу, равному 850 кг. «аштрихованна€ на графике площадь представл€ет собой веро€тность того, что вес наудачу выбранной туши окажетс€ меньше 850 кг, т.е. в интервале от -¥ до 850 кг.
в) Ќайдем веро€тность того, что вес случайно отобранной туши окажетс€ в интервале от 800 до 1300 кг.
ѕо условию: a = 800, b = 1300, а = 950, s = 150.
ƒл€ расчета искомой веро€тности используем формулу расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной величины ’.
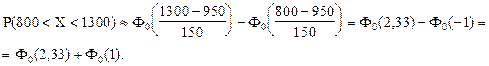
—огласно свойству функции Ћапласа:
-‘0(-1) = ‘0(1).
Ќайдем по таблице функции Ћапласа (ѕриложение 2) значени€ ‘0(z).
‘0(2,33) = 0,49010;
‘0(1) = 0,34134.
ќтсюда: P(800 < X< 1300) = 0,49010 + 0,34134 = 0,83144.
¬еро€тность того, что вес случайно отобранной туши окажетс€ в интервале от 800 кг до 1300 составл€ет 0,83144.
ѕроиллюстрируем решение задачи графически (рис. 5.3).

–ис.5.3. √рафическа€ интерпретаци€ к примеру 5.1.
ѕо условию данной задачи точка на оси абсцисс (z = -1) соответствует х = 800, т.е. весу, равному 800 кг, а точка (z = 2,33) соответствует х = 1300, т.е. весу, равному 1300 кг. «аштрихованна€ на графике площадь представл€ет собой веро€тность того, что вес наудачу выбранной туши окажетс€ в интервале от 800 до 1300 кг.
Ќа графике видно, что искомую веро€тность, что вес наудачу выбранной туши окажетс€ в интервале от 800 до 1300 кг, можно было найти другим способом. ƒл€ этого необходимо было найти веро€тность того, вес наудачу выбранной туши окажетс€ меньше 800 кг, а также- больше 1300 кг, ѕолученные веро€тности Ц сложить и вычесть из единицы.
“ак, веро€тность того, вес наудачу выбранной туши окажетс€ меньше 800 кг - это, другими словами, веро€тность того, что вес случайно отобранной туши окажетс€ в интервале от -¥ до 850 кг.

¬еро€тность того, что вес случайно отобранной туши окажетс€ больше 1300 кг - это, другими словами, веро€тность того, что вес случайно отобранной туши окажетс€ в интервале от 1300 кг до +¥.

ќтсюда, искома€ веро€тность того, что вес наудачу выбранной туши окажетс€ в интервале от 800 до 1300 кг:
–(800 < ’ < 1300) = 1 - (P(X<800) + P(X>1300)) = 1 - (0,15866 + 0,0099) =
=1 - 0,16856 = 0,83144.
г) Ќайдем веро€тность того, что вес случайно отобранной туши отклонитс€ от математического ожидани€ меньше, чем на 50 кг, т.е.:
P(½X - 950½< 50) =?
„то значит: ½X - 950½< 50?
Ёто неравенство можно заменить двойным неравенством:
-50 < X - 950 < 50 или
950 - 50 < X < 950 + 50,
900 < X < 1000.
—ледовательно:
P½X - 950½< 50) = –(900 < ’ < 1000).
ј это веро€тность попадани€ в заданный интервал нормально распределенной случайной величины ’.
ќтсюда:

—огласно свойству функции Ћапласа:
-‘0(-0,33) = ‘0(0,33).
Ќайдем по таблице функции Ћапласа (ѕриложение 2) значени€ ‘0(z).
‘0(0,33) = 0,1293.
—ледовательно:
P(½X - 950½< 50) = –(900 < ’ < 1000) = 2 × 0,1293 = 0,2586.
¬еро€тность того, что вес случайно отобранной туши отклонитс€ от математического ожидани€ меньше, чем на 50 кг, составл€ет 0,2586.
|
|
|
Ёту задачу легче решить, использу€ формулу расчета веро€тности заданного отклонени€ нормально распределенной случайной величины ’ от своего математического ожидани€:

где - D величина отклонени€ случайной величины ’ от математического ожидани€.
ѕо условию D = 50; а = 950, s = 150.
»спользу€ эту формулу, сразу получим:
P(½X - 950½< 50) = 2‘0(50 / 150) = 2‘0(0,33) = 2 × 0,1293 = 0,2586.
ѕроиллюстрируем решение задачи графически (рис. 5.4).

–ис.5.4. √рафическа€ иллюстраци€ к задаче 5.1.
ѕо условию данной задачи точка на оси абсцисс (z = -0,33) соответствует х = 900, т.е. весу, равному 900 кг, а точка (z = 0,33) соответствует х = 1000, т.е. весу, равному 1000 кг. «аштрихованна€ на графике площадь представл€ет собой веро€тность того, что вес наудачу выбранной туши окажетс€ в интервале от 900 до 1000 кг., т.е. отклонитс€ от математического ожидани€ меньше, чем на 50 кг.
д) Ќайдем веро€тность того, что вес случайно отобранной туши отклонитс€ от математического ожидани€ больше, чем на 50 кг, т.е.:
P(½X - 950½> 50) =?
Ёто веро€тность событи€, противоположного по отношению к событию: вес случайно отобранной туши отклонитс€ от математического ожидани€ меньше, чем на 50 кг (P(½X - 950½< 50)).
—ледовательно:
P(½X - 950½> 50) = 1 - P(½X - 950½< 50) = 1 - 0,2586 = 0,7414.
¬еро€тность того, что вес случайно отобранной туши отклонитс€ от математического ожидани€ больше, чем на 50 кг, составл€ет 0,7414.
ћожно использовать другой алгоритм решени€.
¬еро€тность того, что вес случайно отобранной туши отклонитс€ от математического ожидани€ больше, чем на 50 кг, - это веро€тность того, что вес случайно отобранной туши будет или меньше (950 - 50 = 900) кг или больше (950 + 50 = 1000) кг.
ѕо теореме сложени€ веро€тностей несовместных событий имеем:
P(½X - 950½> 50) = P(X < 900) + P(X > 1000).


ќтсюда:
P(½X - 950½> 50) = P(X < 900) + P(X > 1000) = 0,3707 + 0,3707 = 0,7414.
е) Ќайдем границы, в которых отклонение веса случайно отобранной туши от своего математического ожидани€ не превысит утроенного среднего квадратического отклонени€.
¬ этом задании студентам предлагаетс€ проиллюстрировать правило трех сигм, которое можно сформулировать следующим образом:
≈сли случайна€ величина распределена по нормальному закону, то ее отклонение от математического ожидани€ практически не превышает ±3s.
–(½’ - а ½<3s) = 2‘0(3) = 0,9973.
¬еро€тность того, что отклонение нормально распределенной случайной величины ’ от своего математического ожидани€ будет меньше 3s или, другими словами, веро€тность того, что нормально распределенна€ случайна€ величина ’ попадет в интервал (а - 3s; а + 3s), равна 0,9973.
—ледовательно, веро€тность того, что отклонение случайной величины от своего математического ожидани€ по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала и равна 0,0027. ƒругими словами, лишь в 27 случа€х из 10000 случайна€ величина ’ в результате испытани€ может оказатьс€ вне интервала (а - 3s; а + 3s). “акие событи€ считаютс€ практически невозможными.
‘ормулу, описывающую правило трех сигм, несложно получить из формулы веро€тности заданного отклонени€ нормально распределенной случайной величины ’ от своего математического ожидани€:
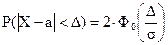
≈сли вз€ть D = 3s, то получим D /s = 3.
ќтсюда:
–(½’ - а ½< 3s) = 2‘0(3) = 0,9973.
|
|
|
ѕо условию задачи: а = 950; s = 150.
ѕравило трех сигм можно представить так:
–(а - 3s < ’ < a + 3s) = 2‘0(3) = 0,9973.
»нтересующие нас границы - это границы интервала (а - 3s; a + 3s), т.е.:
а - 3s< ’ < a + 3s,
950 Ц 3 × 150 < X < 950 + 3 × 150,
500 < X < 1400.
”читыва€, что вес отобранной туши - нормально распределенна€ случайна€ величина, можно быть практически уверенным, что вес случайно отобранной туши не выйдет за пределы от 500 до 1400 кг.
ж) ќпределим границы, в которых с веро€тностью 0,899 будет находитьс€ вес случайно отобранной туши.
‘ормулу веро€тности заданного отклонени€ нормально распределенной случайной величины ’ от своего математического ожидани€ можно представить следующим образом:

или

где g - веро€тность того, что отклонение нормально распределенной случайной величины ’ от своего математического ожидани€ не превысит заданной величины D.
ѕо условию задачи: а = 950; s = 150.
»спользу€ последнюю формулу, получим:
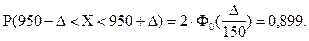
»з соотношени€:  , найдем D.
, найдем D.
 ,
,

ѕо таблице функции Ћапласа (ѕриложение 2) найдем, при каком z = 

z = 1,64, т.е. 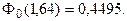
ќтсюда: 
D= 1,64 × 150 = 246.
— веро€тностью 0,899 можно ожидать, что отклонение веса случайно отобранной туши от своего математического ожидани€ не превысит 246 кг.
Ќайдем границы интересующего нас интервала:
а - D < ’ < a + D,
950 - 246 < X < 950 + 246,
704 < X < 1196.
— веро€тностью 0,899 можно ожидать, что вес случайно отобранной туши будет находитьс€ в пределах от 704 до 1196 кг.
ќтвет:а) 0,02275; б) 0,25143; в) 0,83144; г) 0,2586; д) 0,7414;
е) (500; 1400); ж) 246; (704; 1196).
ѕример 5.2. »зменим условие предыдущей задачи.
Ќа рынок поступила крупна€ парти€ гов€дины. ѕредполагаетс€, что вес туш Ц случайна€ величина,
подчин€юща€с€ нормальному закону распределени€ с неизвестным математическим ожиданием и средним квадратическим отклонением s =150 кг. »звестно, что 37,07% туш имеют вес более 1000 кг. ќпределите ожидаемый вес случайно отобранной туши.
–ешение. ѕо условию задачи: s = 150; a = 1000; b = +¥; P(X > 1000) = 0,3707.
ќжидаемый вес случайно отобранной туши - это среднеожидаемый вес, математическое ожидание, т.е. а =?
»спользуем формулу (5.10) расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной величины ’:
 ;
;
 ;
;
 ;
;
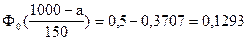 .
.
ѕо таблице функции Ћапласа (ѕриложение 2) найдем, при каком 
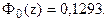
z = 0,33, т.е. 
ќтсюда: 
1000 - а = 0,33 × 150 = 50.
а = 1000 - 50 = 950.
ќтвет. —реднеожидаемый вес случайно отобранной туши составл€ет 950 кг.
ѕример 5.3. ¬новь изменим условие задачи.
Ќа рынок поступила крупна€ парти€ гов€дины. ѕредполагаетс€, что вес туш - случайна€ величина, подчин€юща€с€ нормальному закону распределени€ с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. »звестно, что 15,87% туш имеют вес менее 800 кг. ќпределите среднее квадратическое (стандартное) отклонение веса туш.
–ешение. ѕо условию задачи: а = 950; a = -¥ b = 800; P(X < 800) = 0,1587; s =?
»спользуем формулу (5.10) расчета веро€тности попадани€ в заданный интервал нормально распределенной случайной величины ’:
 ;
;
 ;
;
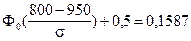 ;
;
 ;
;
 .
.
ѕо таблице функции Ћапласа (ѕриложение 2) найдем, при каком 

z = 1, т.е. 
ќтсюда: 
s= 150.
ќтвет. —реднее квадратическое отклонение веса туш составл€ет 150 кг.
ѕример 5.4. ¬ очередной раз изменим условие задачи.
Ќа рынок поступила крупна€ парти€ гов€дины. ѕредполагаетс€, что вес туш - случайна€ величина, подчин€юща€с€ нормальному закону распределени€ с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. аким должно быть среднее квадратическое (стандартное) отклонение, чтобы с веро€тностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидани€ не превысит 200 кг?
–ешение. ѕо условию задачи: а = 950; D = 200; P(½X - 950½< 200) = 0,81648; s =?
»спользуем формулу (5.11) расчета веро€тности попадани€ заданного отклонени€ нормально распределенной случайной величины ’ от своего математического ожидани€:
“огда получим:
P(½X - 950½< 200) = 2‘0(200 / s) = 0,81648;
2‘0(200 / s = 0,81648;
‘0(200 / s) = 0,81648 / 2;
‘0(200 / s) = 0,40824.
ѕо таблице функции Ћапласа (ѕриложение 2) найдем, при каком 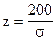

z = 1,33, т.е. 
ќтсюда: 
s = 200 / 1,33 = 150.
ќтвет. „тобы с веро€тностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидани€ не превысит 200 кг, среднее квадратическое отклонение веса туш должно составл€ть 150 кг.
|
|
|
ѕример 5.5 ‘ирма собираетс€ приобрести партию из 100 000 единиц некоторого товара. »з прошлого опыта известно, что 1% товаров данного типа имеют дефекты. акова веро€тность того, что в данной партии окажетс€ от 950 до 1050 дефектных единиц товара?
–ешение. ¬ качестве случайной величины в данной задаче выступает число дефектных единиц товара в общей партии из 100000 единиц. ќбозначим ее через X.
ѕеречислим все возможные значени€ случайной величины ’: 0, 1, 2,..., 99999, 100000.
Ёто - дискретна€ случайна€ величина, т.к. ее возможные значени€ отличаютс€ друг от друга не менее чем на 1, и множество ее возможных значений €вл€етс€ счетным.
ѕо условию веро€тность того, что единица товара окажетс€ дефектной, - посто€нна и составл€ет 0,01 (p = 0,01). ¬еро€тность противоположного событи€, т.е. того, что единица товара не имеет дефекта - также посто€нна и составл€ет 0,99 (q = 1Чp = 1Ч0,01 = 0,99).
¬се 100000 испытаний - независимы, т.е. веро€тность того, что кажда€ единица товара окажетс€ дефектной, не зависит от того, окажетс€ дефектной или нет люба€ друга€ единица товара.
«начени€ случайной величины ’ - это, в общем виде, число по€влений интересующего нас событи€ в 100000 независимых испытани€х.
Ёто позвол€ет сделать вывод о том, что случайна€ величина ’ - число дефектных единиц товара в общей партии из 100000 единиц - подчин€етс€ биномиальному закону распределени€ веро€тностей с параметрами n = 100000 и p = 0,01.
»так, по условию задачи: n = 100000; p = 0,01; q = 0,99, X = m.
Ќеобходимо найти веро€тность того, что число дефектных единиц товара окажетс€ в пределах от m1 = 950 до m2 =1050, т.е. - веро€тность того, что случайна€ величина X = m попадет в интервал от 950 до 1050, т.е.:
P(m1 < m < m2) =?
“ак как мы имеем дело со случайной величиной, подчин€ющейс€ биномиальному распределению, веро€тность по€влени€ событи€ m раз в n независимых испытани€х необходимо вычисл€ть по формуле Ѕернулли (4.9).
¬ данном случае, дл€ определени€ искомой веро€тности нам необходимо с помощью формулы Ѕернулли найти P100000, 950; P100000, 951; P100000, 952;...; P100000, 1049; P100000, 1050, а затем - сложить их, использу€ теорему сложени€ веро€тностей несовместных событий.
ќчевидно, что такой способ определени€ искомой веро€тности св€зан с громоздкими вычислени€ми. “ак, например:
 .
.
ћожно значительно облегчить расчеты, если аппроксимировать биномиальное распределение нормальным, т.е. выразить функции биномиального распределени€ через функции нормального.
огда n - число испытаний в биномиальном эксперименте - возрастает, дискретное биномиальное распределение стремитс€ к непрерывному нормальному распределению. Ёто означает, что дл€ больших n мы можем аппроксимировать биномиальные веро€тности веро€тност€ми, полученными дл€ нормально распределенной случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.
ѕодставим параметры биномиального распределени€ (5.15) в формулу (5.10) и получим формулу дл€ приближенного расчета веро€тности по€влени€ событи€ от m1 и до m2 раз в n независимых испытани€х P(m1 < m > m2):
 ,
,
 , (5.19)
, (5.19)
где ‘ 0(z) - функци€ Ћапласа:  .
.
‘ормулу дл€ приближенного веро€тности по€влени€ событи€ не менее m1 и не более m2 раз в n независимых испытани€х Pn(m1 < m < m2) называют интегральной теоремой Ћапласа.
»спользование локальной и интегральной теорем Ћапласа дает приближенные значени€ искомых веро€тностей. ѕогрешность будет невелика при условии, что
npq > 9.
ƒл€ решени€ данной задачи воспользуемс€ интегральной теоремой Ћапласа:
 ;
;
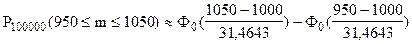 ;
;
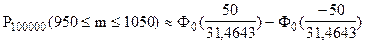 ;
;
 ;
;
 .
.
ѕо таблице функции Ћапласа (ѕриложение 2) найдем ‘0(1,59):
‘0(1,59) = 0,44408.

¬еро€тность того, что в партии из 100000 единиц окажетс€ от 950 до 1050 дефектных единиц товара, составл€ет 0,88816.
ƒанную конкретную задачу можно было решить еще более просто.
ћатематическое ожидание числа дефектных единиц товара равно 1000 единиц:
M(m) = n × p = 100000 × 0,01 = 1000.
јбсолютное отклонение нижней и верхней границ интервала [m1; m2] от математического ожидани€ M(m) = n × p составл€ет 50 единиц:
½m1 Ц n × p½=½950 Ц 100000 × 0,01½= 50;
½m2 - n × p½=½1050 Ц 100000 × 0,01½= 50.
—ледовательно, искомую веро€тность можно рассматривать как веро€тность заданного отклонени€ частоты от своего математического ожидани€:

ѕодставив параметры биномиального распределени€ в формулу расчета веро€тности заданного отклонени€ нормально распределенной случайной величины от своего математического ожидани€, получим формулу дл€ приближенного расчета веро€тности заданного отклонени€ частоты от своего математического ожидани€:

 (5.20)
(5.20)
ѕри использовании этой формулы дл€ решени€ задачи сразу получим:
 ;
;
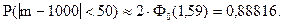
ќтвет. ¬еро€тность того, что в партии из 100000 единиц окажетс€ от 950 до 1050 дефектных единиц товара, составл€ет 0,88816.
ѕример 5.6. ‘ирма собираетс€ приобрести партию из 100 000 единиц некоторого товара. »з прошлого опыта известно, что 1% товаров данного типа имеют дефекты. акова веро€тность того, что в данной партии окажетс€ 1020 дефектных единиц товара?
–ешение. “ак как  , применим локальную теоремућуавра-Ћапласа:
, применим локальную теоремућуавра-Ћапласа:

Ќайдем 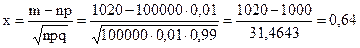 .
.
Ќайдем  (x) по таблице плотности веро€тностей стандартной нормальной случайной величины (ѕриложение 1) -
(x) по таблице плотности веро€тностей стандартной нормальной случайной величины (ѕриложение 1) -  (0,64)=0,3251.
(0,64)=0,3251.

ќтвет. ¬еро€тность того, что в партии из 100000 единиц окажетс€ 1020 дефектных единиц товара, составл€ет 0,0103.
ѕример 5.7. ѕодлежат исследованию 400 проб руды. ¬еро€тность промышленного содержани€ металла в каждой пробе дл€ всех проб одинакова и равна 0,8. Ќайти веро€тность того, что дол€ проб с промышленным содержанием металла отклонитс€ от веро€тности промышленного содержани€ металла в каждой пробе не более чем на 0,05.
–ешение. ¬ отличие от предыдущей задачи, в данном случае речь идет о расчете веро€тности заданного отклонени€ частости (относительной частоты) по€влени€ событи€ от веро€тности его по€влени€ в отдельном независимом испытании, т.е.:

ѕри возрастании числа независимых испытаний распределение частости стремитс€ к нормальному распределению точно так же, как и распределение частоты. Ёто означает, что при больших n мы можем аппроксимировать распределение частости нормальным распределением случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.
ѕодставив параметры распределени€ частости в формулу расчета веро€тности заданного отклонени€ нормально распределенной случайной величины от своего математического ожидани€, получим формулу дл€ приближенного расчета веро€тности заданного отклонени€ частости от своего математического ожидани€ (веро€тности):
ѕараметры распределени€ частости:
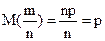 ;
;  ;
; 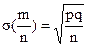 .
.
»спользу€ эти формулы, получим:

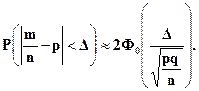 (5.21)
(5.21)
ѕрименим данную формулу дл€ решени€ задачи.
ѕо условию: n = 400; p = 0,8; q = 1- 0,8 = 0,2; D = 0,05.
 ;
;

ќтвет. ¬еро€тность того, что дол€ проб с промышленным содержанием металла отклонитс€ от веро€тности промышленного содержани€ металла в каждой пробе не более чем на 0,05, составл€ет 0,98758.
«адачи к теме 5
1. омпьютерна€ система содержит 50 одинаковых микрочипов. ¬еро€тность того, что любой микрочип будет работать в заданное врем€, равна 0,9. ƒл€ выполнени€ некоторой операции требуетс€, чтобы, по крайней мере, 30 микрочипов было в рабочем состо€нии.
а) „ему равна веро€тность того, что операци€ будет выполнена успешно?
б) „ему равна веро€тность того, что будут работать 47 микрочипов?
2. ѕочтовое отделение быстро оценивает объЄм переводов в рубл€х, взвешива€ почтовые отправлени€, полученные в течение каждого текущего рабочего дн€. ”становлено, что если вес почтовых отправлений составл€ет N кг, то объЄм переводов в рубл€х есть случайна€ величина, распределенна€ по нормальному закону со средним значением 160N и стандартным отклонением 20N руб. Ќайти веро€тность того, что в день, когда вес почтовых отправлений составит 150 кг, объЄм переводов в рубл€х будет находитьс€ в пределах:
а) от 21000 до 27000 руб.; б) более 28500 руб.; в) менее 22000 руб.
3.ћенеджер крупного ресторана по опыту знает, что только 80% людей, сделавших заказ на вечер, придут в ресторан поужинать. ¬ один из вечеров менеджер решил прин€ть 60 заказов, хот€ в ресторане было лишь 55 свободных столиков. „ему равна веро€тность того, что более 55 посетителей придут на заказанные места?
4. Ёкзамен по математической статистике успешно сдают 75% студентов дневного отделени€. ≈сли на втором курсе факультета обучаетс€ 250 студентов, то какова веро€тность того, что 203 студента сдадут экзамен успешно?
5. ¬ отделе продаж страховой компании работают 45 сотрудников. ¬еро€тность того, что сотрудник выполнит план по числу заключенных договоров, оцениваетс€ начальником отдела как 0,7. акова веро€тность того, что:
а) план выполн€т как минимум 35 сотрудников?
б) план выполн€т не более 30 сотрудников?
в) план выполн€т 37 сотрудников?
6. ќтдел маркетинга фармацевтической компании утверждает, что нова€ модификаци€ таблеток от головной боли используетс€ 30% пациентов. ≈сли среди пациентов было отобрано 80 человек, то какова веро€тность того, что отобранна€ дол€ лиц, предпочитающих новую модификацию таблеток, не будет отличатьс€ по абсолютной величине от истинной доли более чем на 0,1?
7. ƒневна€ выручка супермаркета распределена по нормальному закону с математическим ожиданием 10000 у.е. и стандартным отклонением 1400 у.е. Ќайдите веро€тность того, что:
а) выручка супермаркета окажетс€ более 13000 у.е.;
б) выручка супермаркета окажетс€ менее 8000 у.е.;
в) найдите границы, в которых будет находитьс€ выручка супермаркета согласно правилу трех сигм.
8. ѕо данным независимого исследовани€, хлеб определенного сорта, составл€ет 15% от совокупной реализации хлебобулочных изделий. ≈сли выборочному обследованию были подвергнуты 80 торговых предпри€тий, то какова веро€тность того, что дол€ реализации хлеба определенного сорта в генеральной совокупности будет отличатьс€ по абсолютной величине от истинной доли менее чем на 5%?
9. ¬ течение мес€ца кредитным отделом банка было выдано 68 ипотечных кредитов. ћенеджер банка оценивает веро€тность просрочки оплаты таких кредитов как 0,2. акова веро€тность того, что в течение срока кредитовани€ будут просрочены:
а) как минимум 15 кредитов?
б) не более 18 кредитов?
в) 16 кредитов?
10. ‘ирма, занимающа€с€ продажей товаров по каталогу, ежемес€чно получает по почте заказы. „исло этих заказов - нормально распределенна€ случайна€ величина со средним квадратическим отклонением  = 560 и неизвестным математическим ожиданием. ¬ 90% случаев число ежемес€чных заказов превышает 12439. Ќайдите ожидаемое среднее число заказов, получаемых фирмой за мес€ц.
= 560 и неизвестным математическим ожиданием. ¬ 90% случаев число ежемес€чных заказов превышает 12439. Ќайдите ожидаемое среднее число заказов, получаемых фирмой за мес€ц.
11. ƒневна€ добыча угл€ в некоторой шахте распределена по нормальному закону с математическим ожиданием 870 тонн и стандартным отклонением 90 тонн.
а) Ќайдите веро€тность того, что в определенный день будут добыты по крайней мере 900 тонн угл€.
б) ќпределите долю рабочих дней, в которые будет добыто от 860 до 940 тонн угл€.
в) Ќайдите веро€тность того, что в данный день добыча угл€ окажетс€ ниже 750 тонн.
12. андидат на выборах считает, что 20% избирателей в определенной области поддерживают его избирательную платформу. ≈сли 72 избирател€ случайно отобраны из числа избирателей данной области, найдите веро€тность того, что выборочна€ дол€ избирателей, поддерживающих кандидата, не будет отличатьс€ по абсолютной величине от истинной доли более, чем на 0,09.
13. ≈женедельный выпуск продукции на заводе приблизительно распределен по нормальному закону со средним значением, равным 150000 единиц продукции в неделю, и стандартным отклонением - 12000 ед. Ќайдите веро€тность того, что еженедельный выпуск продукции:
а) превысит 170000 единиц;
б) окажетс€ ниже 100000 единиц в данную неделю?
в) ѕредположим, что возникли трудовые споры, и недельный выпуск продукции стал ниже 90000 ед. ћенеджеры обвин€ют профсоюз в беспрецедентном падении выпуска продукции, а профсоюз утверждает, что выпуск продукции находитс€ в пределах прин€того уровн€ (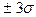 ). ћожно ли довер€ть профсоюзу?
). ћожно ли довер€ть профсоюзу?
14. ¬ес тропического грейпфрута, выращенного в раснодарском крае, - нормально распределенна€ случайна€ величина с неизвестным математическим ожиданием и дисперсией, равной 0,09. јгрономы знают, что 75% фруктов вес€т меньше, чем 0,5 кг. Ќайдите ожидаемый вес случайно выбранного грейпфрута.
15. ќдин из методов, позвол€ющих добитьс€ успешных экономических прогнозов, состоит в применении согласованных подходов к решению конкретной проблемы. ќбычно прогнозом занимаетс€ большое число аналитиков. —редний результат таких индивидуальных прогнозов представл€ет собой общий согласованный прогноз. ѕусть этот прогноз относительно величины банковской процентной ставки в текущем году подчин€етс€ нормальному закону со средним значением а = 11% и стандартным отклонением  = 3,6%. »з группы аналитиков случайным образом отбираетс€ один человек. Ќайдите веро€тность того, что согласно прогнозу этого аналитика уровень процентной ставки:
= 3,6%. »з группы аналитиков случайным образом отбираетс€ один человек. Ќайдите веро€тность того, что согласно прогнозу этого аналитика уровень процентной ставки:
а) превысит 13%;
б) окажетс€ менее 16%;
в) будет в пределах от 13 до 17%.
16. ѕредположим, что в течение года цена на акции некоторой компании есть случайна€ величина, распределенна€ по нормальному закону с математическим ожиданием, равным 50 условным денежным единицам, и стандартным отклонением, равным 10. „ему равна веро€тность того, что в случайно выбранный день обсуждаемого периода цена за акцию будет:
а) более 70 условных денежных единиц?
б) ниже 50 за акцию?
в) между 45 и 58 условными денежными единицами за акцию?
17. ѕо данным университета лишь 45% абитуриентов получают положительные оценки на вступительных экзаменах. ѕредположим, что в приемную комиссию поступило 2120 за€влений. „ему равна веро€тность того, что:
а) хот€ бы 970 абитуриентов получат положительные оценки на вступительных экзаменах?
б) 950 абитуриентов получат положительные оценки на вступительных экзаменах?
18. —редний срок службы коробки передач до капитального ремонта у автомобил€ определенной марки составл€ет 56 мес€цев со стандартным отклонением  = 16 мес. ѕривлека€ покупателей, производитель хочет дать гарантию на этот узел, обеща€ сделать ремонт коробки передач нового автомобил€ в случае ее поломки до определенного срока. ѕусть срок службы коробки передач подчин€етс€ нормальному закону. Ќа сколько мес€цев в таком случае производитель должен дать гарантию дл€ этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?
= 16 мес. ѕривлека€ покупателей, производитель хочет дать гарантию на этот узел, обеща€ сделать ремонт коробки передач нового автомобил€ в случае ее поломки до определенного срока. ѕусть срок службы коробки передач подчин€етс€ нормальному закону. Ќа сколько мес€цев в таком случае производитель должен дать гарантию дл€ этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?
19. ѕри производстве безалкогольных напитков специальный аппарат разливает определенное число унций (1 унци€ = 28,3 г) напитка в стандартную Ємкость. „исло разлитых унций подчин€етс€ нормальному закону с математическим ожиданием, завис€щим от настройки аппарата. оличество унций напитка, разлитых отдельным аппаратом, имеет стандартное отклонение s = 0,4 унции. ѕусть Ємкости объЄмом в 8 унций наполн€ютс€ кока-колой. —колько унций напитка должен в среднем разливать аппарат, чтобы не более 3% Ємкостей оказались переполненными?
20. Ќалогова€ инспекци€ утверждает, что нарушени€ налогового законодательства характерны дл€ 35% предпри€тий города. “щательной проверке были подвергнуты 59 предпри€тий. „ему равна веро€тность того, что дол€ предпри€тий Ц нарушителей будет отличатьс€ от истинной доли более чем на 0,12?






