
“аблица 8.2
ƒл€ построени€ моделей де€тельности оператора, как следует из табл. 8.2, может быть использован раз≠личный математический аппарат.
¬озможности применени€ математических методов в инженерной психологии
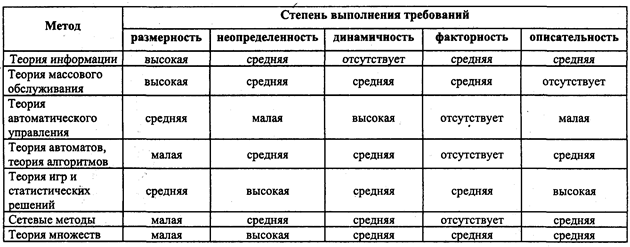
математическим методам в инженерной психо≠логии предъ€вл€ютс€ следующие требовани€: размер≠ность (описание процессов управлени€ со многими неизвестными), динамичность (учет фактора времени), неопределенность (учет случайных, веро€тностных составл€ющих в де€тельности оператора), факторность (учет специфических особенностей поведени€ челове≠ка, например, напр€женности, эмоций и т. п.), описательность (возможность описани€ внутренних, психо≠физиологических механизмов де€тельности человека). роме того, примен€емые методы должны допускать возможность описани€ де€тельности человека и фун≠кционировани€ машины с единых позиций, с помощью единых показателей и характеристик [196]. —равни≠тельна€ характеристика различных методов приведе≠на в табл. 8.2.
»з этой таблицы видно, что метод, одинаково хоро≠шо учитывающий все характеристики де€тельности оператора, практически отсутствует. аждый из рас≠смотренных методов оптимален лишь по одной Чдвум характеристикам, иными словами, удачно описывает лишь определенные стороны де€тельности оператора. ѕоэтому при решении инженерно-психологических задач очень часто приходитс€ примен€ть комбинацию тех или иных методов. Ёто можно сделать, воспользо≠вавшись данными табл. 8.1. и 8.2. –ассмотрим более подробно возможности и особенности применени€ различных математических методов, перечисленных в этих таблицах, дл€ построени€ моделей де€тельности оператора.
8.3. ћатематическое моделирование де€тельности оператора: модели задачи
ћногие из моделей, перечисленные в табл. 8.1. и прежде всего модели первого вида (модели задачи) стро€тс€ на использовании структурного подхода. ѕод ним в общем случае понимаетс€ описание (с помощью определенной системы символов и правил их комби≠наций) взаимосв€зей между различными сторонами (элементами) изучаемого €влени€. ¬ общей психологии разработан р€д моделей дл€ структурного описани€ воспри€ти€, пам€ти, прин€ти€ решени€, процессов коммуникации и т. п. [92]. Ўирокое применение струк≠турный подход находит и в инженерной психологии. ¬ основе его лежит представление де€тельности опе≠ратора в виде определенной последовательности вы≠полн€емых действий. Ќа этой основе базируетс€, на≠пример, обобщенный структурный метод определени€ надежности оператора, к числу структурных относ€т≠с€ и многие из расчетных методов определени€ време≠ни решени€ задачи оператором, на базе структурного подхода осуществл€етс€ алгоритмическое описание и анализ де€тельности оператора, разрабатываютс€ структурно-алгоритмические, сетевые и автоматные модели де€тельности оператора. ƒадим им краткую характеристику.
ѕрименение в инженерной психологии теории автоматов и построение на ее основе моделей де€тель≠ности оператора основано на представлении ее как процесса функционировани€ конечного цифрового (дискретного) автомата [83, 174]. ѕод ним понимаетс€ математическа€ модель различного рода систем, кото≠рые принимают, хран€т и перерабатывают в дискрет≠ном времени дискретную информацию. “акую модель можно примен€ть, если де€тельность оператора пред≠ставл€ет собой дискретный стохастический процесс, состо€щий из отдельных управл€ющих воздействий, формируемых на основании поступающей на сенсор≠ные входы человека информации. ѕоэтому автоматные модели €вл€ютс€ удобным средством представлени€ и описани€ де€тельности управл€ющего типа. »з абст≠рактной теории автоматов известно, что процесс вы≠полнени€ алгоритма (в данном случае Ч де€тельности оператора) математически может быть представлен композицией двух абстрактных автоматов: управл€ю≠щего и операционного (рис. 8.3).
|
|
|

–ис. 8.3. омпозиционна€ автоматна€ (а) и общекибернетическа€ (б) модели де€тельности оператора.
ќперационный автомат A2 непосредственно осу≠ществл€ет необходимые преобразовани€, а управл€ю≠щий автомат A1 управл€ет этими процессами в соот≠ветствии с заложенной программой, исходными данными N0 и случайными внутренними N1 (напри≠мер, ошибки оператора) и внешними N2 факторами, оказывающими вли€ние на временные, точностные и надежностные характеристики де€тельности. “акой подход полностью соответствует общекибернетичес≠кой модели де€тельности.
ƒе€тельность оператора как процесс функциони≠ровани€ дискретного абстрактного автомата может быть представлена следующим образом. јфферентный (от лат. afferens Ч принос€щий) поток дискретной ин≠формации х (считывание показаний приборов, воспри≠€тие команд и т. п.), поступающий на входоператора, переводит его как некоторую управл€ющую систему из состо€ни€ y(t) в состо€ние y(t+1). –езультатом тако≠го преобразовани€ €вл€етс€ дискретный стохастичес≠кий поток эфферентности (от лат. efferens Ч вынос€≠щий) информации z (нажатие кнопки, установка переключателей, доклад и т. д.); при этом система пе≠реходит в новое состо€ние. ƒанный процесс цикли≠чески повтор€етс€ при переходе —„ћ из исходного состо€ни€ H0 в требуемое Ќk, то есть реализуетс€ фун≠кци€ управлени€
 (8.3)
(8.3)
где D Ч совокупна€ де€тельность, которую нужно со≠вершить в системе дл€ перевода ее из состо€ни€ Ќ0 в состо€ние Hk.
јвтоматное представление де€тельности операто≠ра предполагает ее €рко выраженный дискретный характер. Ёто приводит к важному заключению о принципиальной допустимости декомпозиции математичес≠кого описани€ де€тельности оператора. ƒекомпозици€ операционного автомата позвол€ет перейти от решени€ задачи отображени€ (8.3) в общем виде к описанию отдельных подавтоматов, характеризующих элементар≠ные действи€ оператора, что значительно проще. ѕри этом используютс€ промежуточные результаты преоб≠разований HiЦ1 ЧЧЧЧЧЧ>Hi.
«на€ входные сигналы автомата в целом или его отдельных подавтоматов и их функции переходов, мож≠но описать их реакции (действи€ оператора). ¬ простей≠ших случа€х автоматные модели стро€тс€ на основе детерминированных абстрактных автоматов, в более сложных случа€х Ч на основе веро€тностных автома≠тов, функционирование которых в каждом такте рабо≠ты описываетс€ веро€тностными законами.
јвтоматные модели де€тельности оператора об≠ладают р€дом достоинств, среди которых следует от≠метить возможность в равной степени описани€ как машинного, так и человеческого звена в системе Ђче≠ловек-машинаї, простоту построени€ модели, возмож≠ность ее сопр€жени€ с модел€ми других типов. ¬ то же врем€ этим модел€м присущ и р€д недостатков: описание де€тельности с позиций бихевиоризма (от лат. behaviorЧ поведение), т. е. в основе модели ле≠жит простейша€ поведенческа€ формула Ђстимул-ре≠акци€ї, поэтому она не может претендовать на пол≠ную адекватность описани€ реальной де€тельности, поскольку в ней выпадает ее существенный компо≠нент, св€занный с высшей нервной де€тельностью человека, его сознанием и мышлением. ѕоэтому при≠менение автоматных моделей ограничено лишь теми видами де€тельности управл€ющего типа, имеющими жестко алгоритмический характер. ¬озможности мо≠дели могут быть расширены путем применени€ веро≠€тностных моделей и имитационного моделировани€ с помощью Ё¬ћ.
|
|
|
Ќа базе структурного подхода может быть постро≠ена цела€ группа моделей, условно называемых сете≠выми. ¬ основу их построени€ положены те или иные виды сетей. Ќаиболее полно разработаны модели, в основу которых положены традиционные методы се≠тевого планировани€ и управлени€ (—ѕ”). ƒл€ постро≠ени€ сетевой модели де€тельность оператора разбива≠етс€ на р€д отдельных действий, имеющих вполне определенный смысл, например, нажатие кнопки, включение тумблера, движение руки к органу управ≠лени€, перемещение взгл€да, опознание характерис≠тики объекта и т. п. Ќа €зыке сетевых моделей эти действи€ называютс€ работами, а моменты их завер≠шени€ Ч событи€ми. ажда€ работа в конечном итоге должна быть охарактеризована двум€ параметрами Ч математическим ожиданием и дисперсией продолжи≠тельности (времени выполнени€) работы. ќбщее врем€ решени€ задачи оператором равно продолжительности критического пути. ¬ таком виде модель используетс€ дл€ априорной оценки времени решени€ задачи опе≠ратором, а также дл€ описани€ и оптимизации группо≠вой де€тельности операторов [27, 61]. ќсновным дос≠тоинством сетевой модели €вл€етс€ возможность учета последовательно-параллельного характера выполнени€ отдельных действий оператором (группой операторов). ќстальные достоинства и недостатки такие же, как у автоматных моделей.
ѕринципиально новым подходом в теории и прак≠тике сетевых методов €вл€ютс€ функциональные сети [137]. ќни представл€ют собой €зыково-алгебраическую систему дл€ описани€ поведени€ логико-динами≠ческих объектов дискретного типа любой природы, в том числе и де€тельности оператора, функциональные сети €вл€ютс€ обобщением аппарата алгоритмических, автоматных, традиционных сетевых методов; они при≠мен€ютс€ дл€ построени€ математических моделей, позвол€ющих получать веро€тностные и ресурсные (в том числе и временные) характеристики де€тельности оператора.
ѕрименение функциональных сетей позвол€ет перейти от ретроспективных индуктивно-эмпиричес≠ких методов к более прогностичным дедуктивно-формальным методам исследовани€, отражающим как специфические свойства отдельных элементов (и че≠ловека, и машины), так и их системную результатив≠ность и устойчивость функционировани€.
≈ще одной разновидностью сетевых моделей €вл€≠етс€ описание различных управл€ющих действий че≠ловека (более широко Ч его поступков) с помощью фреймов. ‘рейм (от лат. frame Ч рама, скелет) Ч это иерархически упор€доченна€ структура данных, кото≠ра€ €вл€етс€ минимально необходимой дл€ задани€ стереотипных ситуаций или данного класса объектов. ¬ инженерной психологии аппарат фреймов использу≠етс€ дл€ описани€ и анализа ошибочных действий оператора [78].
ƒл€ построени€ сетевых моделей де€тельности опе≠ратора может быть использован также математический аппарат сетей ѕетри [27, 138]. —еть ѕетри представл€≠ет математическую модель дискретных систем с парал≠лельно функционирующими и асинхронно взаимодей≠ствующими компонентами. ѕредложены немецким ученым . ѕетри в начале 60-х гг. √рафически сети ѕетри (рис. 8.4) представл€ют собой двухдольный ори≠ентированный мультиграф с вершинами двух типов: переходами (моделирующими событи€ в дискретной системе) и позици€ми (моделирующими предуслови€ выполнени€ событи€ и постуслови€, возникающие пос≠ле событи€). ѕозиции графически обозначаютс€ кру≠жочками, переходы Ччерточками (рис. 8.4). Ќаправлен≠ное ребро может св€зывать только позицию и переход. роме того, задаетс€ начальна€ разметка позиций: каж≠дой из них сопоставл€етс€ одно из чисел 0, 1, 2... (число маркеров или фишек). Ётим числом моделируетс€ не≠котора€ емкость позиций, количество ресурсов в ней. ѕо отношению к переходам позиции могут быть входными или выходными. Ќекоторый переход t называет≠с€ возбужденным или разрешенным (и может срабо≠тать), если число фишек его входной позиции р не меньше числа ребер, ведущих из р в t. —рабатывание возбужденного перехода заключаетс€ в удалении из каждой его входной позиции р числа фишек, равного числу ребер, ведущих из р в t, и добавлении в каждую его выходную позицию q числа фишек, равного числу ребер, ведущих из t в q. ¬ результате срабатывани€ перехода получаетс€ нова€ разметка сети ѕетри. ƒва возбужденных перехода с общими позици€ми не долж≠ны срабатывать одновременно [166].
|
|
|

–ис. 8.4. √рафическое изображение сети ѕетри.
— помощью сетей ѕетри моделируютс€ не времен≠ные, а причинно-следственные св€зи. ќни широко при≠мен€ютс€ дл€ моделировани€ различных систем. ¬ ин≠женерной психологии их используют дл€ описани€, проектировани€ и исследовани€ де€тельности операто≠ра (группы операторов), определени€ показателей ка≠чества де€тельности, расчета надежности системы Ђче≠ловек-машинаї. Ќапример, в работе [138] сети ѕетри использованы дл€ моделировани€ групповой де€тельно≠сти операторов алгоритмических —„ћ. ƒл€ этого с каж≠дым переходом сети, соответствующим действи€м опе≠ратора, св€зываютс€ соответствующие этому действию математическое ожидание и дисперси€ времени, а так≠же веро€тность его безошибочного выполнени€, а с каждой позицией Ч веро€тность передачи управлени€ от одного действи€ к другому. Ёти характеристики за≠даютс€ с учетом сложности и структуры пультов управ≠лени€ операторов, воздействий факторов внешней сре≠ды, наличи€ напр€женности в де€тельности операторов, вызванной дефицитом времени на выполнение алгорит≠ма. ƒл€ определени€ характеристик де€тельности опе≠ратора сеть представл€етс€ в виде формульной записи. ¬ дальнейшем осуществл€етс€ последовательное сокра≠щение этой записи путем применени€ к каждой из операций формулы соответствующих ей соотношений, которые используютс€ в аналитических методах оцен≠ки веро€тностных характеристик алгоритмов при эле≠ментарных преобразовани€х, упрощающих граф, пред≠ставл€ющий алгоритм.
—обственно моделирование групповой де€тельно≠сти осуществл€етс€ следующим образом. ѕо словесному описанию алгоритма групповой де€тельности (инст≠рукции по эксплуатации) строитс€ сеть ѕетри, отобра≠жающа€ этот алгоритм. ƒл€ этого используетс€ систе≠ма переходов от вершин параллельной граф-схемы алгоритма к фрагментам сети ѕетри. Ќа основе ана≠лиза особенностей групповой де€тельности (наличие операций приема и выдачи команд) сделан вывод о це≠лесообразности расширени€ системы переходов путем введени€ двух дополнительных вершин типа Ђприем командыї и Ђвыдача командыї, что позвол€ет упрос≠тить процедуру алгоритма построени€ сети и процеду≠ру его анализа на корректность. ¬ таком виде сеть ѕетри примен€етс€ дл€ априорной оценки групповой де€тельности по критери€м математического ожидани€ и дисперсии времени выполнени€ алгоритма группой, веро€тности его своевременного и безошибочного выполнени€ [138].
Ќа базе структурного подхода стро€тс€ также ал≠горитмические и структурные модели. јлгоритмичес≠кие модели характеризуютс€ использованием алгорит≠мического €зыка, впервые примененного в инженерной психологии √.ћ. «араковским [52]. ћодели этого клас≠са в принципе могут использоватьс€ дл€ описани€ любой целостной де€тельности, имеющей дискретный характер. ¬ажнейшими ограничени€ми дл€ примене≠ни€ этих моделей служат отсутствие в них операций синтеза и нестохастический характер используемых в них алгоритмов. ѕо этой причине алгоритмические модели имеют в основном лишь дискурсивное (от лат. discursis Ч рассуждение), т. е. формальное, не допус≠кающее расчета применение к сложной целостной де€тельности. ќднако дл€ отдельных видов де€тельно≠сти, дл€ которых удаетс€ построить алгоритм, введены и нормативные дополнени€ [цит. по 178]. ¬ этом слу≠чае они используютс€ дл€ определени€ показателей сложности истереотипности де€тельности оператора. ќсобенно продуктивным применение этих моделей оказываетс€ при использовании нормированных пока≠зателей [10}.
|
|
|
—труктурные модели отображают де€тельность оператора с точки зрени€ ее надежности и эффектив≠ности. ¬ определенной мере эти модели представл€≠ют собой обобщение алгоритмических дл€ совокупно≠сти режимов работы, выполн€емых оператором задач, алгоритмов их решени€, блоков (составл€ющих алго≠ритмы) и конкретных сенсорных, моторных и логи≠ческих операций. —ущественным отличием структур≠ных моделей от алгоритмических €вл€етс€ разработка Ђтиповых блоковї с известными (в общем виде) веро≠€тностными и временными характеристиками. »з таких блоков как из Ђкирпичиковї можно синтезиро≠вать структуры сложной де€тельности и рассчитывать ее веро€тностные и надежностные характеристики. ¬ дальнейшем этот метод трансформировалс€ в фун≠кционально-структурную теорию —„ћ, в основе ко≠торой лежат рассмотренные ранее функциональные сети [137].
¬ р€де случаев модели де€тельности оператора могут строитс€ на базе математического аппарата те≠ории множеств. ѕод ней понимаетс€ раздел математи≠ки, исследующий общее свойство множеств. ћноже≠ством называетс€ любое объединение в одно целое некоторых определенных и различных между собой объектов нашего воспри€ти€ или мысли [166]. “еоре≠тико-множественные модели в инженерной психоло≠гии предложены .—. озловым дл€ описани€ процес≠са информационного поиска оператором, описани€ процессов обучени€; на их основе разработаны элемен≠ты семантической теории информации [70]. —.¬. Ѕори≠сов использовал теоретико-множественную модель дл€ оценки степени неупор€доченности оперативного пол€ пультов управлени€ [10].
ƒальнейшим развитием теоретико-множественно≠го подхода в инженерной психологии €вл€етс€ приме≠нение размытых (нечетких) множеств, пон€тие о кото≠рых введено Ћ. «аде [цит. по 173]. “акой подход основан на том, что ключевые элементы в человеческом мыш≠лении €вл€ютс€ классами объектов, в которых переход от принадлежности к одному классу и непринадлеж≠ности к нему составл€ет непрерывный континуум, и что логика причинно-следственной св€зи в человечес≠ком мышлении отличаетс€ от формальной логики и подчин€етс€ многозначной логике. ласс, который допускает возможность частичного членства, называ≠етс€ размытым, или нечетким, множеством. “акое мно≠жество объектов задаетс€ с помощью функции при≠надлежности, принимающей численные значени€ в диапазоне [0Ч1] в соответствии со степенью принад≠лежности объекта к данному множеству. –азмытое множество характеризуетс€ функцией принадлежнос≠ти mа: u ЧЧЧЧ > 0,1, описывающей каждый элемент uÎU некоторым числом mа (u) из интервала [0 Ц 1].
Ќечеткое множество наиболее адекватно описы≠вают процессы оперативного мышлени€ оператора, поэтому они €вл€ютс€ хорошей моделью дл€ описани€ процессов прин€ти€ решени€ [27, 195], они наход€т применение дл€ описани€ €влений неопределенности, с которой часто сталкиваютс€ при решении различного рода инженерно-психологических задач [184]. »нте≠ресна попытка применени€ √. √. ћаньшиным аппарата нечетких множеств дл€ проведени€ инженерно-психо≠логической оценки —„ћ [173].
8.4. ћатематическое моделирование де€тельности оператора: модели оператора
ћатематические модели, построенные на основе структурного подхода, обладают существенным недо≠статком, заключающемс€ в представлении структуры де€тельности оператора в неизмен€ющемс€, посто€н≠ном виде. (—казанное не относитс€ только к модел€м, в основе которых лежат функциональные сети). ƒл€ преодолени€ этого недостатка √.¬. —уходольским пред≠ложены пон€ти€ веро€тностного алгоритма и случайной структуры, которые реализуютс€ им при построении структурно-алгоритмических моделей де€тельности [111,178]. Ёта модель использует математический ап≠парат теории графов и матричной алгебры и представ≠л€етс€ в виде абстрактного графа де€тельности (рав≠новесного стохастического мультиграфа).
јбстрактный граф де€тельности (ј√ƒ) представл€≠ет собой некоторую конечную совокупность вершин, отображающих элементы де€тельности (людей, пред≠меты и оруди€ труда, реализуемые операции), и сопо≠ставленную этим вершинам совокупность дуг, харак≠теризующих св€зи между элементами де€тельности (материальные, информационные, энергетические). ј√ƒ можно рассматривать как наиболее общую модель де€тельности, поскольку в принципе его дугам и вер≠шинам могут быть приписаны любые качественные и количественные характеристики. ѕри этом дуги ј√ƒ могут быть определены любым математическим и физическим образом. Ѕлагодар€ этому, а также специ≠ально разработанному новому математическому аппа≠рату построени€ веро€тностных алгоритмов и синтеза равновесных мультиграфов оказываетс€ возможным математически описывать практически любую слож≠ную де€тельность, а далее на полученном описании использовать другие известные модели де€тельности.
|
|
|
“ак, рассмотренные выше сервомодели (модели слежени€), основанные на использовании передаточ≠ных функций, могут быть представлены как ориенти≠рованные или неориентированные графы, вершины которых есть условно выдел€емые звень€ (усилитель≠ные, инерционные, дифференцирующие, интегрирую≠щие и т. п.) с известными передаточными свойствами, а дуги (ребра) имеют смысл входных и выходных пе≠ременных. »нформационные модели представл€ют собой подграфы от стохастического орграфа, верши≠ны которого есть веро€тностно характеризуемые при≠знаки, определенные на множестве средств индикации, а также состо€ни€ системы, определ€емые этими при≠знаками, а дуги Ч импликации. “очно также можно показать, что и другие модели де€тельности в конеч≠ном итоге могут быть сведены к ј√ƒ.
“акому графу и его модификаци€м однозначно соответствует р€д матриц: матрица смежности; матри≠ца, описывающа€ веро€тностный алгоритм решени€ каждой задачи в любом из режимов работы; матрица дл€ каждого режима работы; матрица дл€ описани€ работы оператора во всех режимах. »сходной €вл€ет≠с€ матрица смежности, остальные получаютс€ на ее основе с помощью специально введенной операции обобщени€. ѕолученные в матричной форме выраже≠ни€ позвол€ют получить математические модели на разных структурно-алгоритмических уровн€х: реализа≠ции алгоритма, алгоритма задачи, индивидуальной задачи, коллективной задачи. ажда€ из этих моделей может быть построена в двух специфических формах: операционно-логической и предметно-функциональной.
¬ первом случае модель представл€етс€ в виде графа, вершинами которого €вл€ютс€ коды сенсорных, моторных и логических операций, а дугами Ч импли≠кации, характеризуемые частотой. ¬о втором случае модель также представл€етс€ в виде графа. ќднако вершины в нем определены предметно, в виде средств контрол€ и управлени€, а дуги, характеризуемые час≠тотой, определены функционально как пространствен≠ные перемещени€ специалиста, а также в виде посту≠пающей к нему и исход€щей от него информации. Ѕольшое внимание при построении моделей удел€етс€ вопросу получени€ оценок дл€ взвешивани€ частотных алгоритмов и способам синтеза более крупных струк≠тур из подструктур, оптимальных на уровне частных алгоритмов.
¬ разработанных модел€х используютс€: перечис≠ление реализации частных алгоритмов при наиболее веро€тных сочетани€х логических условий; специаль≠ное матричное представление этих реализации и их объединение в виде
 (8.4)
(8.4)
где D Ч надматрица, отображающа€ модель де€тель≠ности дл€ I задач, m режимов работы и n способов решени€ каждой задачи; Arij Ч подматрица j-й реали≠зации i-го частотного алгоритма в r-ом режиме ( ;
;  ;
;  ); Irij, Iri, Ir Ч частота j-го способа i-й задачи и r-го режима работы соответственно.
); Irij, Iri, Ir Ч частота j-го способа i-й задачи и r-го режима работы соответственно.
ѕутем введени€ специальной оценки эффективнос≠ти труда оператора данна€ модель позвол€ет осуществить оптимальную компоновку рабочего места оператора.
ѕомимо использовани€ дл€ построени€ структур≠но-алгоритмических моделей де€тельности оператора теори€ графов используетс€ в инженерной психоло≠гии и дл€ решени€ целого р€да других задач: дл€ оп≠тимального размещени€ людей и машин в рабочих по≠мещени€х и оборудовани€ на рабочем месте [111,178]; дл€ описани€ и анализа потоков информации в систе≠мах контрол€ и управлени€ [135, 178]; дл€ описани€ и машинного моделировани€ процессов пам€ти, опера≠тивного мышлени€ и прин€ти€ решений [151, 100]; дл€ описани€ и анализа организационной структуры тру≠дового коллектива Ч формальной и неформальной [25, 175]. ћетоды теории графов лежат также в основе одного из подходов к построению семантической тео≠рии информации [70].
ƒл€ построени€ моделей оператора может исполь≠зоватьс€ и математический аппарат теории игр; такие модели называютс€ игровыми. “еорией игр называет≠с€ раздел математики, изучающий абстрактные моде≠ли конфликтных ситуаций. ѕод конфликтной понима≠етс€ ситуаци€ (игра), в которой участвуют как минимум два игрока (лица, коллективы, управл€ющие системы), стрем€щиес€ по некоторым определенным в игре пра≠вилам обеспечить себе максимальный выигрыш. »н≠тересы игроков полностью или частично противопо≠ложны, то есть вс€кое улучшение положени€ одного игрока ухудшает положение другого- ѕростейшей схе≠мой теории игр €вл€етс€ конечна€ игра двух лиц с нулевой суммой. ѕри этом каждый игрок независимо от другого выбирает одну из конечного числа возмож≠ностей. аждой паре выбранных возможностей соот≠ветствует некоторый выигрыш одного игрока, равный проигрышу другого, то есть сумма выигрышей обоих игроков равна нулю. ÷ель теории игр заключаетс€ в выработке рекомендаций дл€ определени€ оптималь≠ной стратегии каждого из участников игры. ¬се реко≠мендации выбираютс€ в предположении, что против≠ник €вл€етс€ разумным и делает все дл€ того, чтобы помешать игроку добитьс€ своей цели. ѕоэтому воз≠можности применени€ теории игр дл€ создани€ моде≠лей де€тельности оператора весьма ограничены, по≠скольку он, как правило имеет дело с неразумным Ђпротивникомї. ¬ этом плане весьма спорным €вл€ет≠с€ утверждение о том, что одним из наиболее перспек≠тивных направлений развити€ моделировани€ дл€ проектировани€ де€тельности человека €вл€етс€ ис≠пользование математического аппарата теории игр [55]. сожалению, реальное положение дел не соот≠ветствует этому утверждению.
ќдна из самых первых и наиболее удачных игро≠вых моделей в инженерной психологии была предло≠жена ¬.‘. ¬ендой дл€ описани€ процесса технической диагностики (поиска отказов) человеком-оператором [17]. ћодель базируетс€ на следующих исходных ус≠лови€х. ќператор получает сигнал об отклонении ре≠жима от нормы. —уществует п параметров, проверка значений которых позвол€ет установить причину от≠клонени€ и компенсировать его одним из имеющихс€ способов. „ем быстрее оператор найдет причину, тем быстрее он ликвидирует отклонение; при каждой не≠удачной попытке Ч вызове Ђпустогої параметра или неудачном опережающем действии Ч оператор Ђпла≠титї потерей времени и, возможно, дальнейшим ухуд≠шением состо€ни€ объекта. ¬ыигрыш и потер€ могут быть в каждом случае оценены количественно.
ƒл€ нахождени€ оптимальной стратегии операто≠ра необходимо найти оптимальную перестановочную матрицу; ее размер 2nхn2. „исло последовательных шагов дл€ получени€ достаточно хорошего приближе≠ни€ равно nm, где m Ч небольшое положительное чис≠ло, такое что nm<n!. ѕроцедура технической диагнос≠тики сводитс€ к одномерному варианту игры и состоит в следующем: 1 Ч оператор (игрок 1) пытаетс€ опре≠делить какой из п параметров определ€ет наличие не≠исправности; 2 Ч параметр (игрок 2) скрыт в одном из п сигнальных элементов устройства отображени€.
»гра продолжаетс€ до нахождени€ параметра (иг≠рока 2), обозначенного как выигрыш оператора (игро≠ка 1). Ёту процедуру можно представить как поиск набора положительных чисел d; (чем длиннее пере≠бор параметров, тем меньше выигрыш оператора, если же оператор не успевает предотвратить аварию и она происходит, это рассматриваетс€ как выигрыш игрока 2). ≈сли параметр скрыт в i-м сигнальном элементе с веро€тностью хi, то оператор стремитьс€ выбрать такое i, при котором aixi= 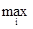 (aixi), где аi Ч есть кака€-либо оценка эффективности i-го действи€ оператора.
(aixi), где аi Ч есть кака€-либо оценка эффективности i-го действи€ оператора.
ћатематический аппарат теории игр предлагаетс€ также использовать в качестве основного средства дл€ описани€ и разрешени€ различного рода конфликтов в системе Ђчеловек-машинаї [131]. «десь приведена классификаци€ возможных конфликтов, даетс€ их под≠робное математическое описание, показаны в общем виде пути их разрешени€. ќдним из основных путей предлагаетс€ использовать возможность преобразова≠ни€ неорганизованного конфликта в организованный. –ассмотрение этого вопроса ведетс€ с позиций разви≠ваемого автором данной работы организмического под≠хода к проектированию и построению —„ћ. сожале≠нию, предлагаемые игровые модели нос€т очень общий и абстрактный характер, а пути их практической реали≠зации и примеры практического применени€ никоим образом не привод€тс€.
Ќаиболее широкое применение в насто€щее врем€ дл€ описани€ де€тельности оператора наход€т методы теории информации, теории массового обслуживани€, теории автоматического управлени€. ѕолучаемые на основе использовани€ этих методов модели де€тельно≠сти называютс€ соответственно информационными, сервисными (или модел€ми обслуживани€), модел€ми слежени€. –ассмотрим их более подробно.
ѕрименение теории информации дл€ моделирова≠ни€ де€тельности оператора основано на представле≠нии его в качестве канала св€зи, задачей которого €вл€етс€ передача информации со средств отображе≠ни€ на органы управлени€. ѕостроение модели осно≠вано на расчете количества информации по формулам (2.2) и (2.3). ќни представл€ют собой наиболее общие формулы дл€ расчета количества информации.
ќднако оператор в своей де€тельности выполн€ет различные действи€ (поиск сигнала, считывание пока≠заний с прибора, производство вычислений, управл€≠ющие движени€ т. п.). ƒл€ каждого из этих действий в зависимости от конкретных условий их выполнени€ могут быть получены частные формулы дл€ определе≠ни€ количества информации.
ƒл€ получени€ частных формул необходимо вос≠пользоватьс€ двум€ основными правилами.
1. оличество информации характеризует сложность выбора одного состо€ни€ из n возможных. ѕоэтому в любом частном случае нахождени€ количе≠ства информации прежде всего необходимо опре≠делить общее число возможных состо€ний данной системы и их веро€тности, а затем применить формулу (2.2) при неравноверо€тных или (2.3) при равноверо€тных состо€ни€х системы.
2. величине информации применимо правило адап≠тивности. Ёто означает, что общее количество ин≠формации, поступающей от нескольких источников, равно суммарному количеству информации от каж≠дого источника в отдельности. ѕравило справедли≠во, если все источники взаимонезависимы. ѕриме≠нительно к де€тельности оператора это означает, что дл€ определени€ общего количества информации, перерабатываемой человеком, необходимо вначале определить количество информации, используемой при выполнении каждого действи€, а затем найден≠ные значени€ просуммировать.
ѕор€док применени€ этих правил рассмотрим на частном примере. Ќа рис. 8.5 показана лицева€ сторо≠на измерительного прибора, имеющего три диапазона измерений: 50 ¬, 100 ¬ и 500 ¬. ќпределим количество информации, которую перерабатывает оператор, про≠вод€ измерение на каждом из диапазонов.
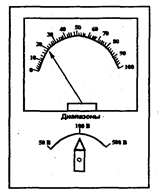
–ис. 8.5. Ћицева€ панель измерительного прибора.
Ќа первом диапазоне оператор снимает отсчет с прибора и найденное значение делит на два. ≈сли погрешность сн€ти€ показаний равна ±d, то общее число различимых оператором состо€ний прибора равно
 (8.5)
(8.5)
где ’max и Xmin Ч соответственно максимальное и ми≠нимальное значение шкалы прибора.
—чита€, что величина 5 равна половине цены деле≠ни€ шкалы и что все показани€ равноверо€тны, из формулы (2.3) следует
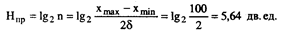
Ќайденное показание оператор должен разделить на два. оличество информации, используемой при вычислении, находитс€ по формуле
 (8.6)
(8.6)
где Ni Ч максимально возможные значени€ использу≠емых при вычислении чисел; m Ч количество чисел, используемых при вычислении; R Ч максимально воз≠можное значение результата вычислени€.
Ќетрудно заметить, что формула (8.6) получена на основании приведенных выше правил. ≈е применение основано на том, что при производстве вычислений человек m раз производит выбор нужного числа из N, возможных, а при получении результата Ч выбор од≠ного числа из R возможных.
ѕодставл€€ исходные данные в формулу (8.6), по≠лучим: Ќвыч = lg2l00 + lg22 + lg250 = 13,28 дв.ед.
ќбщее количество перерабатываемой информации равно H1 =Hпр + Hвыч = 5,64 + 13,28 = 18,92 дв.ед.
–ассмотренна€ стратеги€ поведени€ характерна дл€ оператора малообученного или оператора, который сравнительно редко производит измерени€ на данном диапазоне. ≈сли же оператор часто работает с прибо≠ром, то у него могут быть сформированы и хранитьс€ в пам€ти эталоны истинных значений дл€ каждого значени€ шкалы прибора. “огда действие по переводу отсчета со шкалы в истинное значение практически будет отсутствовать, выполн€тьс€ автоматически на уровне навыка, внимание оператора на его выполне≠ние специально не будет направлено. ѕри каждом отсчете оператор будет извлекать из пам€ти хран€щиес€ там эталоны истинных значений измер€емого по≠казател€ и использовать их дл€ получени€ конечного результата без производства специальных вычислений. ќчевидно, количество перерабатываемой человеком информации будет определ€тьс€ только той величиной, которую оператор получает производ€ отсчет по шка≠ле прибора, т. е. в этом случае Hi = 5,64 дв. ед.
ак видим, информационные методы не всегда дают однозначный ответ о результатах де€тельности оператора. ƒаже реша€ одну и ту же задачу, человек может примен€ть различные стратегии поведени€. Ёто существенно вли€ет на количество информации, пере≠рабатываемой при решении задачи.
ѕри работе на втором диапазоне оператор сразу получает истинное значение измер€емого показател€, т. е. Ќ2 = 5,64 дв. ед. ѕри работе на третьем диапазоне оператор помимо сн€ти€ отсчета должен умножить полученное значение на п€ть. –асчет количества ин≠формации производитс€ аналогично тому, как это де≠лалось дл€ первого диапазона.
ћетоды теории информации примен€ютс€ в инже≠нерной психологии при решении р€да задач. ¬о-первых, количество перерабатываемой информации может ис≠пользоватьс€ как мера сложности работы оператора, следовательно, такой способ позвол€ет сравнивать меж≠ду собой различные виды операторской де€тельности. ¬о-вторых, зна€ количество информации, можно оценить врем€, которое затрачивает оператор на переработку этой информации, поскольку между ними, как правило, существует линейна€ зависимость. ¬-третьих, знание количества информации позвол€ет согласовать скорость ее выдачи (производительность источника информации) с психофизиологическими возможност€ми человека по ее приему и обработке. ”словием неискаженной пере≠дачи информации €вл€етс€: Vпос < Vоп, где Vпос Ч ско≠рость поступлени€ информации к оператору; Vоп Ч про≠пускна€ способность оператора.
¬еличина Vоп зависит от характера де€тельности оператора. ≈сли он может быть представлен как канал без пам€ти, то величина пропускной способности ле≠жит в пределах 10Ч70 дв.ед/с. ¬ этом случае человек работает как простой канал передачи информации, последовательные сигналы независимы друг от друга, предыдущий сигнал не вли€ет на прием следующего (печатание на машинке, корректорска€ работа, выпол≠нение арифметических операций и т. п.).
≈сли в процессе де€тельности оператору необ≠ходимо запомнить отрезок входной последовательно≠сти сигналов, не превышающий объем кратковре≠менной пам€ти, то в этом случае человека можно рассматривать как канал переработки информации с кратковременной пам€тью. ѕропускна€ способ≠ность имеет в этом случае пор€док нескольких дв. ед. в секунду (примерно 2Ч4 дв. ед/с). “акой режим €вл€етс€ наиболее характерным дл€ де€тельности оператора.
≈сли же отрезок входной информации превышает объем кратковременной пам€ти, то дл€ его запомина≠ни€ необходимо многократное повторение. ѕропускна€ способность вследствие этого падает до дес€тых долей дв. ед. в секунду и ниже [111].
ѕрименение теории информации дл€ анализа де≠€тельности оператора св€зано с целым р€дом трудно≠стей. Ёто обусловлено тем, что теори€ информации была создана дл€ решени€ р€да задач в технике св€зи. ѕоэтому простой перенос ее методов в другую об≠ласть Ч исследование человеческой де€тельности Ч не всегда дает желаемые результаты.
ќсновные причины трудностей применени€ тео≠рии информации дл€ изучени€ де€тельности операто≠ра заключаютс€ в следующем:
1. ¬ основе расчета количества информации по форму≠лам (2.2) и (2.3) лежит длина физического алфавита сигналов и веро€тностей их по€влени€. „еловек же зачастую пользуетс€ собственным (внутренним) алфа≠витом сигналов, отличным от физического, а субъек≠тивные веро€тности сигналов дл€ человека не всегда совпадают с объективными. ќднако принципы фор≠мировани€ субъективного алфавита еще до конца не раскрыты. ѕоэтому приходитс€ пользоватьс€ неко≠торой идеализированной моделью де€тельности че≠ловека, в основу которой положены характеристики входных, а не Ђвнутреннихї сигналов человека.
2. “еори€ информации занимаетс€ лишь стационар≠ными процессами, статистические характеристики которых с течением времени не мен€ютс€. ’а≠рактеристики же человека ввиду его обучаемости, утомл€емости, действи€ различных факторов бес≠прерывно мен€ютс€ во времени.
3. “еори€ информации не учитывает смысловую сто≠рону информации, ее ценность и значимость. Ќа де€тельность же оператора оказывают вли€ние не только статистические характеристики сигналов, но и их смысл и значение дл€ оператора.
4. “еори€ информации не учитывает временную нео≠пределенность сигналов. ƒл€ человека же имеет большое значение не только то, какие сигналы и с какой веро€тностью к нему поступают, но и врем€ их поступлени€ [155]. Ёто €вл€етс€ источ≠ником дополнительной неопределенности, котора€ при анализе де€тельности, как правило, не учи≠тываетс€.
Ќаличие этих трудностей накладывает существен≠ные ограничени€ на применение теории информации в инженерной психологии. »гнорирование их приво≠дит к значительному разбросу экспериментальных данных и затрудн€ет сопоставление результатов, по≠лученных в разных исследовани€х. ќднако это не дол≠жно €вл€тьс€ причиной отказа вообще от применени€ информационных методов в инженерной психологии. ак и любой другой, информационный метод справед≠лив лишь при определенных услови€х и дл€ решени€ определенных задач. Ёти услови€ в общем виде сво≠д€тс€ к следующему:
Х четко определен алфавит используемых человеком сигна≠лов и веро€тности их по€влени€;
Х сигналы по своему смысловому значению примерно рав≠ноценны дл€ оператора;
Х характеристики работоспособности оператора в преде≠лах изучаемого отрезка времени не претерпевают суще≠ственных изменений;
Х стратеги€ поведени€ оператора известна и не мен€етс€ в процессе решени€ однотипных задач;
Х число поступающих к оператору различных сигналов не≠велико, сами сигналы слабо завис€т ƒруг от друга;
Х временна€ неопределенность сигналов существенно мень≠ше смысловой неопределенности или же она может быть учтена при расчетах количества информации.
¬ тех случа€х, когда эти услови€ соблюдены, при≠менение теории информации дл€ изучени€ и описани€ де€тельности оператора дает весьма полезные резуль≠таты [122, 168, 207]. Ќар€ду с этим делаютс€ интенсив≠ные попытки совершенствовани€ информационных методов применительно к анализу и описанию де€тель≠ности оператора. Ёти попытки идут как по пути совер≠шенствовани€ существующих методов, использующих энтропийные оценки количества информации, так и по пути учета семантической стороны информации.
Ќапример, в работе [155] существенно расшир€≠етс€ пон€тие энтропии по сравнению с рассмотрен≠ными выше случа€ми. ѕри этом считаетс€, что любой сигнал индикатора как источника информации может полезно служить задачам контрол€ и управлени€ лишь в том случае, если он будет соотнесен ко времени его по€влени€ и экспозиции. “аким образом, дл€ де€тель≠ности оператора важна не только статистическа€ (ча≠стота по€влени€), но и временна€ (врем€ по€влени€) неопределенность. ¬ силу этого возникает необходи≠мость €вного введени€ времени в исходные соотноше≠ни€ дл€ оценки энтропии и количества информации. — математической точки зрени€ этот шаг эквивалентен переходу от уровн€ случайных событий на уровень случайных процессов в моделировании взаимодей≠стви€ человека и машины.
ѕри таком подходе в качестве основы дл€ формиро≠вани€ выражений энтропии и количества информации необходимо рассматривать веро€тности наступлени€ тех или иных событий Xi в интересующий нас момент ti на отрезке времени наблюдени€ 0 £ t £ T, т. е. веро€тности – (хi, t). “огда дл€ полной количественной характеристи≠ки неопределенности ситуации с учетом неопределенно≠сти, вносимой фактором времени, будем иметь
 (8.7)
(8.7)
—реднее количество информации в сообщении, вырабатываемом на отрезке наблюдени€, составит
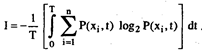 (8.8)
(8.8)
Ќахождение веро€тностей – (хi, t) €вл€етс€ специ≠фической задачей и определ€етс€ типом и характером протекани€ процесса управлени€, а также теми требо≠вани€ми, которые предъ€вл€ютс€ к де€тельности опе≠ратора.
Ёнтропи€ сообщени€ и определ€емое ею количе≠ство информации определ€етс€ по формулам (2.2) и (2.3). ак уже отмечалось, эти формулы оценивают энтропию взаимно независимых сообщений. »ными словами, предполагаетс€, что по€вление того или ино≠го сообщени€ не измен€ет веро€тность по€влени€ сле≠дующего сообщени€. ќднако при работе оператора в —„ћ такой случай не всегда возможен. ак правило, поступающа€ последовательность сигналов обладает логической избыточностью. Ёто означает, что по€вле≠ние определенного сигнала измен€ет веро€тность по≠€влени€ следующего сигнала. Ќаличие логической избыточности равносильно уменьшению энтропии, поскольку по€вление определенного сигнала хi умень≠шает неопределенность очередного состо€ни€ инфор≠мационной модели.
ѕри подсчете количества поступающей в этом случае информации необходимо пользоватьс€ форму≠лами условий энтропии. “ак, например, энтропи€ вто≠рого и третьего пор€дка равна
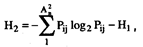 (8.9)
(8.9)
 (8.10)
(8.10)
где –ij и Pijk Ч веро€тности по€влени€ всех возможных диграмм и триграмм сигналов (совместного по€влени€ двух и трех сигналов); H1 Ч энтропи€ первого пор€дка, определ€ема€ по формуле (2.2); 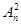 ,
,  Ч максималь≠но возможное число диграмм и триграмм сигналов, рав≠ное числу размещений по два и по три из общего числа n сигналов.
Ч максималь≠но возможное число диграмм и триграмм сигналов, рав≠ное числу размещений по два и по три из общего числа n сигналов.
‘ормула (8.9) выражает среднюю энтропию сиг≠нала при условии, что уже известен предыдущий, фор≠мула (8.10) Ч энтропию сигнала, если известны два предыдущих. ѕодобным образом можно вычислить и энтропию более высоких пор€дков [119].
ƒл€ построени€ моделей де€тельности оператора может использоватьс€ также математический аппарат теории массового обслуживани€. —труктурна€ схема системы массового обслуживани€. (—ћќ) с человеком-оператором показана на рис. 8.6. »нформаци€ со средств отображени€ и от взаимодействующих опера≠торов, а также сигналы внешней среды образуют вхо≠д€щий поток за€вок (требований на обслуживание). ќбычно предполагаетс€, что вход€щий поток подчинен закону ѕуассона. “акой поток иначе называетс€ про≠стейшим. ƒл€ его описани€ требуетс€ знать величину lk Ч плотность вход€щего потока, котора€ равн€етс€ числу за€вок, поступивших в единицу времени. «а€вки поступают или пр€мо к оператору, или станов€тс€ в очередь на обслуживание (если оператор зан€т обслу≠живанием предыдущей за€вки). ”стройством дл€ хра≠нени€ очереди могут быть средства отображени€ ин≠формации или пам€ть оператора. ¬ зависимости от организации очереди могут быть различные типы —ћќ: с ожиданием, или без потерь (люба€ за€вка хранитс€ до тех пор, пока не будет обслужена оператором); с ограниченным ожиданием (за€вка хранитс€ в очереди ограниченное врем€); с ограниченной длиной очереди (в очередь может становитьс€ лишь ограниченное чис≠ло за€вок); с потер€ми (за€вки, поступившие в момент зан€тости оператора, в очередь не станов€тс€ и к об≠служиванию не принимаютс€).

–ис. 8.6. —труктурна€ схема системы массового обслуживани€ с человеком-оператором.
ќрганизаци€ очереди определ€етс€ характером де€тельности оператора. ѕоэтому при проектировании де€тельности следует стремитьс€, чтобы она, насколь≠ко это возможно, была организована по схеме массового обслуживани€ с ожиданием. ѕри прочих равных услови€х это позвол€ет обеспечить максимальную эффективность функционировани€ —„ћ.
«а€вки, поступившие к оператору, обрабатывают≠с€ им по заданному алгоритму. ачественна€ сторона обслуживани€ (правильно или неправильно обработа≠на информаци€, с какими затратами сил и средств, какой психофизиологической Ђценойї и т. п.) в теории массового обслуживани€ не учитываетс€: здесь значе≠ние имеет факт поступлени€ или непоступлени€ за€в≠ки на обслуживание.
“аким образом, в данной модели оператор пред≠ставл€етс€ в качестве обслуживающего аппарата —ћќ. ќсновной его характеристикой €вл€етс€ врем€ обслу≠живани€, в теории массового обслуживани€ оно обыч≠но принимаетс€ подчиненным экспоненциальному закону распределени€. ƒл€ построени€ закона распре≠делени€ необходимо знать интенсивность обслужива≠ни€ m, котора€ €вл€етс€ величиной, обратной средне≠му значению времени обслуживани€.
’арактер обслуживани€ за€вок может быть одно≠канальным или многоканальным, однофазным или многофазным. ѕри многоканальном обслуживании вход€щий поток распредел€етс€ между несколькими операторами. ѕри многофазном обслуживании посту≠пивша€ за€вка обслуживаетс€ аппаратом первой фазы (первым оператором), затем передаетс€ на дальнейшее обслуживание во вторую фазу (следующему операто≠ру) и т. д.
ѕрименение аппарата теории массового обслужи≠вани€ позвол€ет учесть р€д специфических особеннос≠тей, характерных дл€ де€тельности оператора и обуслов≠ленных представлением его в качестве обслуживающего аппарата. “ак, например, ограниченность объема опера≠тивной пам€ти заставл€ет рассматривать —ћќ с ограни≠ченной длиной очереди, а ограниченность длительности сохранени€ информации в пам€ти Ч —ћќ с ограничен≠ным временем ожидани€. √руппова€ де€тельность опе≠раторов может быть учтена при рассмотрении многока≠нальных или многофазных —ћќ в зависимости от вида взаимодействи€ операторов.
¬озможность совершени€ ошибок оператором и их исправлени€ приводит к необходимости рассмотрени€ —ћќ с ненадежным обслуживающим аппаратом. ѕри этом ошибки оператора рассматриваютс€ как поток отказов обслуживающего аппарата, а врем€ их исправ≠лени€ Ч как врем€ восстановлени€.
ѕрименение теории массового обслуживани€ по≠звол€ет решить многие вопросы организации де€тель≠ности человека-оператора. их числу относитс€ опре≠деление необходимого числа операторов, определение требований к уровню подготовленности оператора (обученности, скорости реакций, объему пам€ти и т.д.), определение допустимой плотности потока сигналов, поступающих к оператору, решение некоторых задач организации взаимодействи€ операторов. ѕредставл€≠етс€ возможность вычислени€ веро€тностей различных состо€ний системы Ђчеловек-машинаї. —ледовательно, так же как и теори€ информации, теори€ массового обслуживани€ дает количественные методы описани€ де€тельности человека-оператора.
сожалению, применение методов теории массо≠вого обслуживани€ дл€ построени€ моделей де€тель≠ности оператора также св€зано с целым р€дом трудно≠стей. ќсновна€ из них определ€етс€ введением целого р€да ограничений относительно вида вход€щего пото≠ка за€вок и закона распределени€ времени обслужи≠вани€. ¬ход€щий поток на практике часто отличаетс€ от простейшего, а закон распределени€ времени об≠служивани€ Ч от экспоненциального. ƒруга€ труд≠ность св€зана с тем, что в теории массового обслужи≠вани€ не учитываетс€ качественна€, содержательна€ сторона обслуживани€. ƒл€ оценки качества обслужи≠вани€ необходимо дополнительно примен€ть другие методы.
Ёти трудности ограничивают область применени€ аналитических методов теории массового обслужива≠ни€. ќднако так же, как дл€ теории информации, это не должно €вл€тьс€ причиной дл€ полного отказа от применени€ этих методов в инженерной психологии. ”слови€ их применени€ здесь свод€тс€ к следующему:
Х поступающа€ к оператору информаци€ должна допус≠кать интерпретацию ее в терминах вход€щего потока за€≠вок;
Х вход€щий поток и врем€ обслуживани€ должны подчи≠н€тьс€ определенным законам распределени€;
Х вход€щий поток должен быть однородным, в противном случае должно быть возможным разделение его на одно≠родные группы (по срочности, важности, затратам на об≠служивание и т. п.);
Х дл€ отражени€ динамического характера процесса обслу≠живани€ должна быть установлена система критериаль≠ных временных функций, позвол€юща€ оценить эффек≠тивность —ћќ на нестационарных режимах работы.
ѕри соблюдении этих условий возможно приме≠нение методов теории массового обслуживани€ дл€ анализа де€тельности оператора в —„ћ [70, 113, 155, 162,168].
ƒл€ построени€ математических моделей де€тель≠ности-оператора в системах непрерывного типа (транс≠портные средства: самолет, автомобиль, корабль; систе≠мы, в которых оператор выполн€ет функции слежени€ или наведени€; системы регулировани€ параметров, работающие с участием человека, и т. п.) могут приме≠н€тьс€ методы теории автоматического управлени€ (“ј”). — позиций “ј” человек-оператор рассматрива≠етс€ как элемент след€щей системы, какой представ≠л€етс€ в данном случае система Ђчеловек-машинаї. Ќа работу системы вли€ют динамические св€зи элемен≠тов системы друг с другом и человеком.
ѕроцесс анализа системы состоит из трех этапов:
Х установление критери€ поведени€ замкнутой системы и определение ее передаточной функции;
Х нахождение такой передаточной функции оператора, ко≠тора€ позволила бы получить требуемую функцию всей системы;
Х проведение системы меропри€тий (отбор, тренировка операторов, соответствующее оформление технической части —„ћ), обеспечивающих требуемую функцию опе≠ратора.
ѕри решении этих задач необходимо учитывать следующие психофизиологические особенности чело≠века: ограниченность полосы пропускани€, одноканальность, недостаточную точность работы, неста≠бильность коэффициента усилени€, внесение помех и т. п. ак правило, учесть все эти особенности быва≠ет трудно, поэтому на практике используют лишь упрощенные модели де€тельности оператора. ќдной из них €вл€етс€ линейна€ модель, структурна€ схемаее показана на рис. 8.7. Ќа этой схеме оператор пред≠ставл€етс€ в виде трех последовательно соединенных звеньев. ѕервое звено осуществл€ет прием сигналов; по своим динамическим свойствам оно €вл€етс€ уси≠лительным звеном с запаздыванием. ¬торое звено Ч решающее (вычислительное). ѕри достаточной трени≠ровке, отсутствии возмущающих воздействий и мини≠мальной психофизиологической напр€женности опера≠тора это звено представл€ет собой обычный усилитель. “ретье звено оператора Ч исполнительное. ѕо своим свойствам оно €вл€етс€ инерционным звеном.

–ис. 8.7. —труктурна€ схема линейной модели.
ќбща€ передаточна€ функци€ такой модели опе≠ратора может быть записана как произведение пере≠даточных функций отдельных звеньев
 (8.11)
(8.11)
где k = k1k2k3 Ч коэффициент усилени€ оператора; t1 Ч врем€ реакции оператора, равное в среднем 0,2 с; t2 Ч посто€нна€ времени, характеризующа€ инерцию (примерно 0,125 с) в образовании исполнительного дей≠стви€.
Ќаиболее важным недостатком существующих мо≠делей, основанных на использовании аппарата “ј”, €вл€етс€ их линейность. ћежду тем хорошо известно, что человек-оператор €вл€етс€ сугубо нелинейным зве≠ном след€щей системы. ƒл€ удовлетворительного опи≠сани€ де€тельности оператора с учетом этого замеча≠ни€ необходимо применение градиентных методов.
√лава IX. »ћ»“ј÷»ќЌЌџ≈ ћ≈“ќƒџ
9.1. ‘изическа€ (психологическа€) имитаци€ де€тельности оператора
Ўирокое место в арсенале методов инженерной психологии занимают имитационные методы. ¬ыделе≠ние их в отдельную группу €вл€етс€ несколько услов≠ным, поскольку их в р€де случаев трудно отделить от психологических или математических методов. ¬ то же врем€, как указывалось в главе V, этим методам при≠сущи специфические особенности, что и позвол€ет, хот€ бы и условно, выделить имитационные методы в осо≠бую группу.
¬ самом общем плане имитаци€ (от лат. imitatio Ч подражание, подделка) может быть определена как воспроизведение характеристик некоторой системы, ситуации, событи€ или €влени€ в обстановке, отлич≠ной от той, в которой протекает реальна€ де€тельность оператора [ 105]. —редства, с помощью которых может быть достигнуто это воспроизведение, могут быть фи≠зическими или символическими (в частности, цифро≠выми). физическа€ имитаци€ может быть такой точ≠ной, что ее бывает трудно отличить от оригинала, который она имитирует. ѕримером этого могут быть различного рода военные учени€. —имволическа€ имитаци€ может быть достаточно полной копией про≠текающих в оригинале процессов, но нагл€дного сход≠ства с ним в этом случае обычно не бывает. ѕримером этого €вл€етс€ моделирование реальных процессов методом статистических испытаний (метод ћонте- арло).
»митаци€ де€тельности оператора (грудам опера≠торов) может быть частичной или полной. ‘изическа€ имитаци€, как правило, имеет частичный характер, по≠скольку, хот€ физические характеристики процесса или системы можно воспроизвести достаточно полно, опе≠ративные услови€ де€тельности не поддаютс€ такому полному воспроизведению. ѕри полной имитации ха≠рактеристики системы, окружающей среды вместе с их входными сигналами и ответными реакци€ми пред≠ставлены символически, посредством математических выражений. ¬се операции этой математической сис≠темы выполн€ютс€ вычислительной машиной с помо≠щью метода статистических испытаний [105]. ѕри этом различают аналитическое имитационное моделирова≠ние и статистическое имитационное моделирование [137]. »х особенности и основные отличи€ будут рас≠смотрены ниже.
ѕомимо рассмотренного, ј.». Ќафтульев предла≠гает различать динамическую и цифровую имитацию. ѕерва€ протекает в реальном, втора€ Ч в ускоренном масштабе времени. ќсновное отличие динамической имитации от цифровой заключаетс€ в основном в том, что в первом случае человек как бы непосредственно выполн€ет (имитирует) свои функции, а во втором Ч основные его функции имитируютс€ с помощью Ё¬ћ. ѕодытожива€ все сказанное следует отметить, что фи≠зическа€ имитаци€ обычно носит частичный характер и осуществл€етс€ в реальном масштабе времени; сим≠волическа€ имитаци€, напротив, может носить более полный характер и протекает в ускоренном масштабе времени.
¬ажнейшей формой физической имитации €вл€ет≠с€ делова€ игра. ќна представл€ет метод имитации управленческих и деловых ситуаций путем игры по заданным правилам человека (группы людей) и Ё¬ћ. ƒелова€ игра €вл€етс€ формой воссоздани€ предмет≠ного и социального содержани€ профессиональной де€тельности, моделировани€ систем отношений, ха≠рактерных дл€ данного вида практики. ѕроведение деловой игры представл€ет собой развертывание осо≠бой (игровой) де€тельности участников на имитацион≠ной модели, воссоздающей услови€ и динамику произ≠водства. ¬ зависимости от того, какой тип человеческой практики воссоздаетс€ в игре и каковы цели участников, различают деловые игры учебные, исследователь≠ские, управленческие, аттестационные. ƒеловые игры получили широкое распространение в св€зи с задача≠ми по совершенствованию управлени€, прин€ти€ пла≠новых и производственных решений, подготовки и повышени€ квалификации кадров. ”чебна€ делова€ игра позвол€ет задать в обучении предметный и соци≠альный контексты будущей профессиональной де€≠тельности и тем самым смоделировать более адекват≠ные по сравнению с традиционным обучением услови€ формировани€ личности специалиста. ¬ этих услови€х усвоение нового знани€ накладываетс€ на канву буду≠щей профессиональной де€тельности; обучение при≠обретает совместный, коллективный характер; форми≠рование специалиста осуществл€етс€ в результате подчинени€ двум типам норм: нормам компетентных предметных действий и нормам отношений в группо≠вой де€тельности. ћотиваци€, интерес и эмоциональ≠ный статус участников деловой игры обусловливаютс€ широкими возможност€ми дл€ целеполагани€ и целеосуществлени€, диалогического общени€ на материа≠ле проблемно представленного содержани€ деловой игры. ¬ инженерной психологии деловые игры широ≠ко примен€ютс€ дл€ подготовки операторов энергоси≠стем, в психологии управлени€ Ч дл€ подготовки раз≠личного рода управленческих кадров.
–ассмотрим более подробно на конкретных при≠мерах возможные случаи применени€ деловых игр дл€ решени€ указанных задач.
¬ работе [197] обоснована необходимость форми≠ровани€ оперативных навыков и умений Ч заключи≠тельного этапа подготовки операторов энергоблоков Ч посредством деловых (оперативных) игр. ƒл€ этого в оперативной де€тельности персонала энергоблоков было выделено игровое начало, найден подлинный соревновательный элемент. Ќапример, обучаемому поручалась роль энергоблока, и он должен был пра≠вильно реагировать на управл€ющие действи€ друго≠го обучаемого. »ли один из игроков Ђизобретает ава≠риюї, а другой игрок Ч устран€ет отказы. ѕомимо этого разработаны сценарии дл€ проведени€ оператив≠ных игр при возникновении тех или иных ситуаций в технологическом процессе.
Ёто позволило создать не просто игровую обучаю≠щую систему, но прежде всего Ч игровую тренирую≠щую систему. ƒанный аспект €вл€етс€ принципиаль≠но важным, так как позвол€ет ликвидировать разрыв между знани€ми и умени€ми, между обучением и тре≠нировкой. “ренирующее качество именно и достигну≠то посредством оперативных игр. ƒл€ решени€ этих задач разработано несколько разновидностей таких игр: ситуационные (наблюдение, диагностика, планирова≠ние), координационные (взаимодействие с автомати≠кой), противоаварийные.
–ассмотрение особенностей проведени€ таких игр обсудим дл€ случа€ диагностики [197]. Ё¬ћ задает исходные услови€ и предлагает обучаемому указать вид игры (стандартна€, усложненна€, ускоренна€ и облегченна€). ƒопустим, выбрана усложненна€ игра. ќт обучаемого требуетс€ в этом случае показать пони≠мание технологической ситуации и ее многомерности. «атем Ё¬ћ просит обучаемого найти причину откло≠нени€. ¬ случае правильной диагностики в рамках за≠данного лимита времени Ё¬ћ фиксирует победу обу≠чаемого.
≈сли же правильное решение прин€то с опоздани≠ем, машина разрешает продолжить игру с добавкой времени. ќтказ от добавки ведет к фиксации проигры≠ша и повтору игры дл€ другой ситуации; согласие на дополнительное врем€ увеличивает штрафные очки, что не ведет к чистой победе, но и не исключает ничью. ничьей ведет также правильное решение, прин€тое воврем€, но с помощью Ё¬ћ. ѕроигрыш фиксируетс€ в случае ошибки обучаемого. ќт проигрыша следует отличать поражение, которое засчитываетс€ обучаемо≠му, если он прин€л ошибочное решение, от€гощенное просрочкой времени, невзира€ на помощь. ѕоражение вводит в действие дополнительные игры. ќни дел€тс€ на две группы: игры с признаками и игры с причина≠ми (табл. 9.1).
“аблица 9.1
ƒополнительные игры

»з игр с признаками особенно существенной €в≠л€етс€ игра ЂЌайти приборыї. –ечь идет о проверке Ђпрочностиї св€зей между наименовани€ми признака и его индикаторами. ¬ каждой группе дополнительных игр предусмотрены взаимные переходы. „то касаетс€ игр с причинами, то здесь особенно интересна игра Ђќчиститьї. ѕроведенные эксперименты с оператора≠ми электростанций показали особую трудность указан≠ной фильтрации даже дл€ опытных операторов. »гра состоит в максимально быстром выделении ложных причин, причем количество баллов, получаемых игро≠ком, тем больше, чем выше правдоподобие ложной причины [197].
ак уже отмечалось ранее, деловые игры наход€т широкое применение и при отработке управленческих решений по инженерно-психологическому (эргоно≠мическому) обеспечению новых образцов техники. ќдин из вариантов такой игры описан в [199]. ¬ ней моделируетс€ организаци€ взаимодействи€ предпри≠€ти€ промышленности (заказчика) и разработчика по организации работ по инженерно-психологическому (эргономическому) обеспечению разработки, испыта≠ний и внедрению новой техники.
»з рассмотренных примеров видно, что физичес≠кое имитационное моделирование, осуществл€емое в форме деловых и учебных игр, направлено не только на исследование и изучение оперативной и управлен≠ческой де€тельности, но и на обучение и тренировку оперативного и управленческого персонала, отработ≠ку ими соответствующих навыков и умений. ¬ этом плане деловые игры выступают не столько как элемент исследовательской де€тельности, сколько они €вл€ют≠с€ одной из форм обучени€ и тренировок персонала.
9.2. ÷ифрова€ (статистическа€) имитаци€ де€тельности оператора
–ассмотренные ранее методы в р€де случаев не могут быть использованы дл€ изучени€ и анализа де≠€тельности оператора. ”кажем некоторые из этих слу≠чаев.
1. ѕрименение математических методов в процессе проектировани€ —„ћ, как правило, позвол€ет лишь приближенно оценивать де€тельность оператора, поскольку эти методы не позвол€ют учесть целый р€д особенностей де€тельности оператора. ѕопыт≠ки учета этих особенностей привод€т к существен≠ному усложнению модели. ѕри этом может получить≠с€, что аналитическое решение задачи оказываетс€ либо принципиально невозможным, либо св€занным с большими теоретическими и вычислительными трудност€ми.
2. ѕрименение экспериментальных методов в про≠цессе испытаний и эксплуатации —„ћ также не всегда оказываетс€ возможным. Ёто может быть св€зано с опасностью дл€ здоровь€ или жизни людей, невозможностью экспериментального вос≠произведени€ некоторых ситуаций, с большой сложностью или стоимостью эксперимента.
¬ этих случа€х весьма полезные результаты дает применение статистического моделировани€. ќно ба≠зируетс€ на методе статистических испытаний (метод ћонте- арло). ћетод основан на розыгрыше (имита≠ции) воздействи€ случайных факторов на де€тельность оператора и функционирование —„ћ непосредствен≠но в ходе моделировани€. Ётим объ€сн€етс€ другое название метода Ч имитационное моделирование.
—мысл метода заключаетс€ в многократной реа≠лизации с помощью Ё¬ћ моделируемого процесса. ажда€ реализаци€ носит случайный характер. ƒос≠товерность окончательного решени€ достигаетс€ ста≠тистической обработкой промежуточных результатов по множеству реализации.
»з этого следует, что имитационные методы зани≠мают промежуточное положение между эксперимен≠тальными и математическими методами. ѕо способу получени€ данных о де€тельности оператора метод €вл€етс€ математическим, а по характеру их получе≠ни€ и использовани€ он копирует экспериментальный метод. ѕоэтому имитационные методы называют так≠же машинным или математическим экспериментом.
ѕрименение имитационных методов позвол€ет избежать многих недостатков экспериментальных и математических методов. — одной стороны, имитацион≠ные методы позвол€ют получить сравнительно высо≠кую достоверность результатов моделировани€ уже на ранних этапах проектировани€ —„ћ. — другой сторо≠ны, по выражению академика ¬.ћ. √лушкова, матема≠тический эксперимент работает и в тех случа€х, когда эксперименты с реальными объектами сильно затруд≠нены, а порой и вовсе невозможны [29]. роме того, в р€де случаев его стоимость может оказатьс€ гораздо ниже, чем стоимость эксперимента.
¬ насто€щее врем






